Démonstration de la formule de Leibniz

Démonstration de la formule de Leibniz

Formule de Leibniz

En mathématiques, plusieurs identités portent le nom de formule de Leibniz, nommées d'après le mathématicien Gottfried Wilhelm Leibniz (21 juillet 1646 - 14 novembre 1716) :

  • En analyse réelle, la formule de Leibniz est la formule donnant les dérivées successives d'un produit de fonctions réelles d'une variable réelle. La formule de Leibniz désigne aussi une formule plus générale du calcul différentiel donnant la différentielle du produit de deux fonctions différentiables à valeurs dans une algèbre normée.
  • Par extension, la formule de Leibniz, aussi appelée identité de Leibniz, désigne abusivement une identité que doivent vérifier par définition les dérivations.
  • En algèbre linéaire, la formule de leibniz fournit une définition du déterminant d'une matrice comme une somme alternée sur ses serpents.
  • Enfin, la formule de Leibniz désigne aussi la somme de la série alternée des inverses des entiers impairs.

Dérivée d'un produit

Articles détaillés : Dérivée et Règle du produit.

Le produit de deux fonctions d'une variable réelle f et g définies et dérivables jusqu'à l'ordre n sur un intervalle I est dérivable jusqu'à l'ordre n. La formule de Leibniz fournit sa dérivée d'ordre n donnée par :

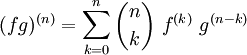
(f g)^{(n)} = \sum_{k=0}^n \binom{n}{k} \ f^{(k)}\ g^{(n-k)}

où les nombres entiers 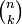\tbinom{n}{k} sont les coefficients binomiaux.

Cette formule se démontre par récurrence sur l'entier n. La démonstration est comparable à celle de la formule du binôme de Newton. Cette dernière peut d'ailleurs en être déduite.

En choisissant par exemple f = exp(ax) et g = exp(bx) on a f.g = exp((a + b)x).

Démonstration

Procédons par récurrence sur n.

Pour n = 1 la formule est vraie car

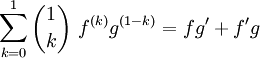
\sum_{k=0}^1 \binom{1}{k} \ f^{(k)}g^{(1-k)}=fg'+f'g

qui est vrai selon la dérivée d'un produit de fonctions dérivables.

Supposons la formule vraie au rang n, alors :

\begin{align} (fg)^{(n+1)} &= \left( \sum_{k=0}^n \binom{n}{k} f^{(k)} g^{(n-k)} \right)' \\ &= \sum_{k=0}^n \binom{n}{k} f^{(k+1)} g^{(n-k)} + \sum_{k=0}^n \binom{n}{k} f^{(k)} g^{(n-k+1)} &\mathrm{(r\grave{e}gles \ de \ d\acute{e}rivation)}\\ &= \sum_{l=1}^{n+1} \binom{n}{l-1} f^{(l)} g^{(n+1-l)} + \sum_{k=0}^n \binom{n}{k} f^{(k)} g^{(n+1-k)} &\mathrm{(changement \ d'indice)}\\ &= \sum_{l=1}^{n} \binom{n}{l-1} f^{(l)} g^{(n+1-l)} + \sum_{k=1}^n \binom{n}{k} f^{(k)} g^{(n+1-k)} + \binom{n}{0} f^{(0)} g^{(n+1)} + \binom{n}{n} f^{(n+1)} g^{(0)} \\ &= \sum_{k=1}^{n} \left[ \binom{n}{k-1} + \binom{n}{k} \right] f^{(k)} g^{(n+1-k)}+ f^{(0)} g^{(n+1)} + f^{(n+1)} g^{(0)} \\ &= \sum_{k=1}^{n} \binom{n+1}{k} f^{(k)} g^{(n+1-k)} + f^{(0)} g^{(n+1)} + f^{(n+1)} g^{(0)} &\left(\text{car} \ \tbinom{n}{k-1} + \tbinom{n}{k}=\tbinom{n+1}{k}\right) \\ (fg)^{(n+1)} &= \sum_{k=0}^{n+1} \binom{n+1}{k} f^{(k)} g^{(n+1-k)} &\mathrm{(rajout \ des \ termes \ }k=0 \text{ et } k=n+1\text{)} \\ \end{align}

La formule est donc vraie pour n + 1. Par récurrence, elle est vraie pour tout n.

Note : on peut aussi démontrer la formule de Leibniz en utilisant un développement de Taylor sans reste intégral.

Série alternée

Article détaillé : Série alternée.

La formule de Leibniz est un exemple de série alternée :

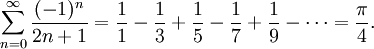
\sum_{n=0}^{\infty} \frac{(-1)^n}{2n+1} = \frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots = \frac{\pi}{4}.

Elle a été découverte en Occident au XVIIe, mais apparaît déjà chez Madhava, mathématicien indien de la province de Kerala, vers 1400. Les travaux mathématiques indiens de cette période ne seront connus en Occident qu'à la fin du XIXe siècle, pendant la colonisation de l'Inde par la Grande-Bretagne.

Démonstration

Considérons la série géométrique infinie,

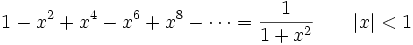
1 - x^2 + x^4 - x^6 + x^8 - \cdots = \frac{1}{1+x^2} \qquad |x| < 1

C'est la limite de

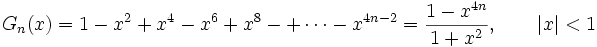
G_n(x)=1 - x^2 + x^4 - x^6 + x^8 -+ \cdots - x^{4n-2}= \frac{1-x^{4n}}{1+x^2}, \qquad |x| < 1

En écrivant que

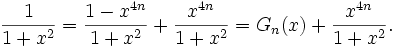
\frac{1} {1+x^2}=\frac{1-x^{4n}}{1+x^2}+\frac{x^{4n}}{1+x^2}=G_n (x)+ \frac{x^{4n}}{1+x^2}.

on obtient, en intégrant de chaque côté entre 0 et 1,

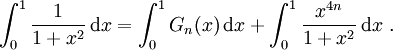
\int_{0}^{1} \frac{1} {1+x^2}\, \mathrm dx= \int_{0}^{1}G_n(x)\, \mathrm dx+\int_{0}^{1}\frac{x^{4n}}{1+x^2}\, \mathrm dx \ .

Dans le membre de droite, l'intégrale de Gn(x) donne la somme recherchée et l'autre intégrale converge vers 0 à la limite 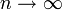n \rightarrow \infty puisque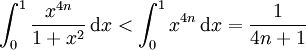

\int_{0}^{1}\frac{x^{4n}}{1+x^2} \, \mathrm dx< \int_{0}^{1} x^{4n}\,\mathrm dx=\frac{1}{4n+1} \

Le membre de gauche,

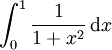
\int_{0}^{1} \frac{1} {1+x^2}\, \mathrm dx

vaut arctan(1) − arctan(0) = π⁄4, on a donc

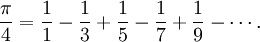
\frac{\pi}{4} = \frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots.

Déterminant d'une matrice carrée

Le déterminant d'une matrice carrée A = (aij) d’ordre n est le nombre noté det(A) égal à :

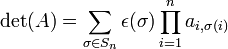
\det(A)=\sum_{\sigma \in S_n}\epsilon(\sigma) \prod_{i=1}^n a_{i, \sigma(i)}

où Sn est l’ensemble des permutations de {1,2,...,n} et pour une permutation σ de Sn, ε(σ) désigne sa signature ; égale à 1 si la permutation est paire et -1 si la permutation est impaire.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Formule de Leibniz ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Démonstration de la formule de Leibniz de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Demonstration de la formule de Leibniz — Formule de Leibniz En mathématiques, plusieurs identités portent le nom de formule de Leibniz, nommées d après le mathématicien Gottfried Wilhelm Leibniz (21 juillet 1646 14 novembre 1716) : En analyse réelle, la formule de Leibniz est la… …   Wikipédia en Français

  • Démonstration De La Formule De Leibniz — Formule de Leibniz En mathématiques, plusieurs identités portent le nom de formule de Leibniz, nommées d après le mathématicien Gottfried Wilhelm Leibniz (21 juillet 1646 14 novembre 1716) : En analyse réelle, la formule de Leibniz est la… …   Wikipédia en Français

  • Démonstration de la formule de leibniz — Formule de Leibniz En mathématiques, plusieurs identités portent le nom de formule de Leibniz, nommées d après le mathématicien Gottfried Wilhelm Leibniz (21 juillet 1646 14 novembre 1716) : En analyse réelle, la formule de Leibniz est la… …   Wikipédia en Français

  • Formule De Leibniz — En mathématiques, plusieurs identités portent le nom de formule de Leibniz, nommées d après le mathématicien Gottfried Wilhelm Leibniz (21 juillet 1646 14 novembre 1716) : En analyse réelle, la formule de Leibniz est la formule donnant les… …   Wikipédia en Français

  • Formule de leibniz — En mathématiques, plusieurs identités portent le nom de formule de Leibniz, nommées d après le mathématicien Gottfried Wilhelm Leibniz (21 juillet 1646 14 novembre 1716) : En analyse réelle, la formule de Leibniz est la formule donnant les… …   Wikipédia en Français

  • Formule de Leibniz — Pour les articles homonymes, voir Règle de Leibniz. En mathématiques, plusieurs identités portent le nom de formule de Leibniz, nommées d après le mathématicien Gottfried Wilhelm Leibniz : En analyse réelle, la formule de Leibniz est la… …   Wikipédia en Français

  • Formule de Leibnitz — Formule de Leibniz En mathématiques, plusieurs identités portent le nom de formule de Leibniz, nommées d après le mathématicien Gottfried Wilhelm Leibniz (21 juillet 1646 14 novembre 1716) : En analyse réelle, la formule de Leibniz est la… …   Wikipédia en Français

  • Formule Du Binôme De Newton — La formule de Newton est une formule mathématiques donnée par Isaac Newton pour trouver le développement d une puissance entière quelconque d un binôme. Elle est aussi appelée formule du binôme de Newton, ou plus simplement formule du binôme.… …   Wikipédia en Français

  • Formule du binome de Newton — Formule du binôme de Newton La formule de Newton est une formule mathématiques donnée par Isaac Newton pour trouver le développement d une puissance entière quelconque d un binôme. Elle est aussi appelée formule du binôme de Newton, ou plus… …   Wikipédia en Français

  • Formule du binôme — de Newton La formule de Newton est une formule mathématiques donnée par Isaac Newton pour trouver le développement d une puissance entière quelconque d un binôme. Elle est aussi appelée formule du binôme de Newton, ou plus simplement formule du… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”