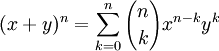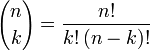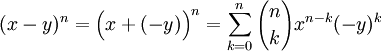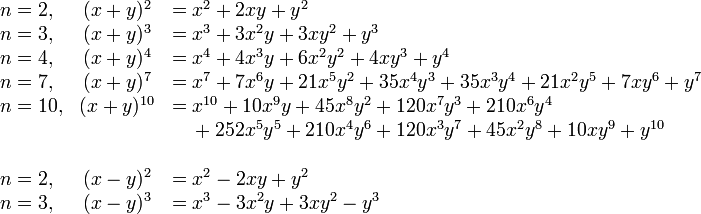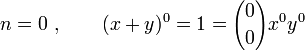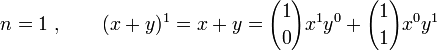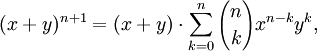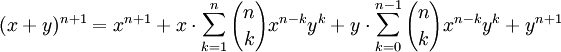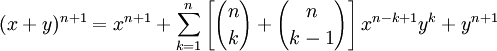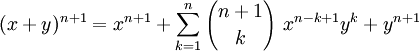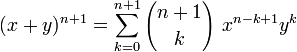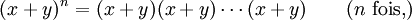Formule du binome de Newton

Formule du binôme de Newton

La formule de Newton est une formule mathématiques donnée par Isaac Newton pour trouver le développement d'une puissance entière quelconque d'un binôme. Elle est aussi appelée formule du binôme de Newton, ou plus simplement formule du binôme.

Énoncé

Soit un binôme composé des termes x et y défini sur un anneau (par exemple deux nombres réels ou complexes, deux matrices, etc.) qui commutent (c'est-à-dire tels que xy = yx) et un entier naturel n,

$(x+y)^n=\sum_{k=0}^n {n \choose k} x^{n-k} y^k$

où les nombres

${n \choose k}=\frac{n!}{k!\,(n-k)!}$

(parfois aussi notés 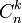$C_n^k$ ) sont les coefficients binomiaux.

Remplacer dans la formule y par -y revient à prendre le second terme comme négatif :

$(x-y)^n=\Big(x+(-y)\Big)^n=\sum_{k=0}^n {n \choose k} x^{n-k} (-y)^k$

Exemples :

$\begin{array}{lcl}n=2,& (x + y)^2 &= x^2 + 2xy + y^2\\ n=3,& (x + y)^3 &= x^3 + 3x^2y + 3xy^2 + y^3\\ n=4,& (x + y)^4 &= x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4\\ n=7,& (x + y)^7 &= x^7+7x^6y+21x^5y^2+35x^4y^3+35x^3y^4+21x^2y^5+7xy^6+y^7\\ n=10,& (x + y)^{10} &= x^{10}+10x^9y+45x^8y^2+120x^7y^3+210x^6y^4\\&&\quad {}+252x^5y^5+210x^4y^6+120x^3y^7+45x^2y^8+10xy^9+y^{10}\\ \\ n=2,& (x - y)^2 &= x^2 - 2xy + y^2\\ n=3,& (x - y)^3 &= x^3 - 3x^2y + 3xy^2 - y^3\\ \end{array}$

Démonstration

Soient x, y des éléments d'un anneau tels que xy=yx et n un entier naturel.

$(x+y)^n=\sum_{k=0}^n {n \choose k} x^{n-k} y^k$

Démontrons cette formule par récurrence.

Initialisation

$n=0~,\qquad(x+y)^0=1={0 \choose 0}x^0y^0$

$n=1~,\qquad(x+y)^1= x + y ={1 \choose 0}x^1y^0 + {1 \choose 1}x^0y^1$

Caractère héréditaire

Soit n un entier supérieur ou égal à 1, montrons que si la relation est vraie pour n, elle l'est aussi pour n+1 :

Par hypothèse de récurrence :

$(x+y)^{n+1}=(x+y)\cdot\sum_{k=0}^n {n \choose k} x^{n-k} y^k,$

Par distributivité de $\cdot$ sur $+$ :

$(x+y)^{n+1}=x^{n+1}+x\cdot\sum_{k=1}^n {n \choose k} x^{n-k} y^k +y\cdot\sum_{k=0}^{n-1} {n \choose k} x^{n-k} y^k + y^{n+1}$

Par factorisation :

$(x+y)^{n+1} =x^{n+1}+\sum_{k=1}^n \left\lbrack {{n} \choose {k}} + {{n} \choose {k-1}} \right\rbrack x^{n-k+1} y^{k}+ y^{n+1}$

En utilisant la formule du triangle de Pascal :

$(x+y)^{n+1} =x^{n+1}+\sum_{k=1}^n {{n+1}\choose k}~x^{n-k+1} y^{k}+y^{n+1}$

$(x+y)^{n+1} =\sum_{k=0}^{n+1} {{n+1}\choose k}~x^{n-k+1} y^{k}$

Ce qui termine la démonstration.

Variantes

Une ébauche de preuve beaucoup plus intuitive utilise le fait que le coefficient binomial 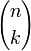${n \choose k}$ est le nombre de parties à $k$ éléments dans un ensemble à $n$ éléments. Quand on développe l'expression

$(x+y)^n=(x+y)(x+y)\cdots(x+y)\qquad (n \text{ fois,})$

on obtient une somme de monômes de la forme $x p y q$ où $p$ et $q$ représentent respectivement le nombre de fois qu'on a choisi $x$ ou $y$ en développant. On a forcément $p + q = n$ , puisqu'à chaque fois qu'on ne choisit pas $x$ , on choisit $y$ . 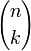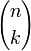Enfin, comme il y a ${n \choose k}$ manières différentes de choisir $k$ fois la valeur $x$ parmi les $n$ expressions $(x + y)$ multipliées ci-dessus, le monôme $x k y n - k$ doit apparaître dans le développement avec le coefficient ${n \choose k}$ .

On peut également déduire la formule du binôme de la Formule de Leibniz.

Anecdote

Le Professeur Moriarty, ennemi du célèbre Sherlock Holmes, aurait publié un article sur le binôme de Newton^[1].

Notes et références

↑ Arthur Conan Doyle, Le Dernier problème, 1891

Articles connexes

Portail des mathématiques

Ce document provient de « Formule du bin%C3%B4me de Newton ».

Catégories : Analyse combinatoire | Isaac Newton

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Formule du binome de Newton de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Formule Du Binôme De Newton — La formule de Newton est une formule mathématiques donnée par Isaac Newton pour trouver le développement d une puissance entière quelconque d un binôme. Elle est aussi appelée formule du binôme de Newton, ou plus simplement formule du binôme.… … Wikipédia en Français
Formule du binôme de newton — La formule de Newton est une formule mathématiques donnée par Isaac Newton pour trouver le développement d une puissance entière quelconque d un binôme. Elle est aussi appelée formule du binôme de Newton, ou plus simplement formule du binôme.… … Wikipédia en Français
Formule du binôme de Newton — La formule de Newton est une formule mathématique donnée par Isaac Newton[1] pour trouver le développement d une puissance entière quelconque d un binôme. Elle est aussi appelée formule du binôme de Newton, ou plus simplement formule du binôme.… … Wikipédia en Français
Formule Du Multinôme De Newton — En mathématiques, la formule du multinôme de Newton est une relation donnant le développement d une puissance entière n d une somme d un nombre fini m de termes sous forme d une somme de produits de puissances de ces termes affectés de… … Wikipédia en Français
Formule du multinome de Newton — Formule du multinôme de Newton En mathématiques, la formule du multinôme de Newton est une relation donnant le développement d une puissance entière n d une somme d un nombre fini m de termes sous forme d une somme de produits de puissances de… … Wikipédia en Français
Formule du multinôme de newton — En mathématiques, la formule du multinôme de Newton est une relation donnant le développement d une puissance entière n d une somme d un nombre fini m de termes sous forme d une somme de produits de puissances de ces termes affectés de… … Wikipédia en Français
Formule Du Trinôme De Newton — En mathématiques, la formule du trinôme de Newton ou plus simplement la formule du trinôme est une relation donnant le développement d une puissance d une somme de trois termes en monômes. Pour tous nombres réels ou complexes a, b et c, et pour… … Wikipédia en Français
Formule du trinome de Newton — Formule du trinôme de Newton En mathématiques, la formule du trinôme de Newton ou plus simplement la formule du trinôme est une relation donnant le développement d une puissance d une somme de trois termes en monômes. Pour tous nombres réels ou… … Wikipédia en Français
Formule du trinôme de newton — En mathématiques, la formule du trinôme de Newton ou plus simplement la formule du trinôme est une relation donnant le développement d une puissance d une somme de trois termes en monômes. Pour tous nombres réels ou complexes a, b et c, et pour… … Wikipédia en Français
Formule du trinôme de Newton — En mathématiques, la formule du trinôme de Newton ou plus simplement la formule du trinôme est une relation donnant le développement d une puissance d une somme de trois termes en monômes. Pour tous nombres réels ou complexes a, b et c, et pour… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Formule du binome de Newton

Formule du binôme de Newton

Sommaire

Énoncé