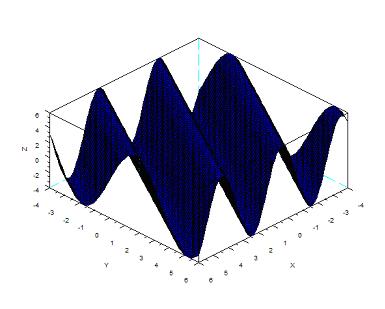
- Démonstration de l'équation modélisant une onde sinusoïdale
-
Démonstration de la formule modélisant une onde sinusoïdale
Une onde sinusoïdale peut se modéliser avec cette formule :
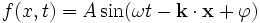
Démonstration
L’étude de la propagation d’une déformation peut se faire dans deux référentiels, celui du lieu d’observation (Galiléen) xy, ou celui de l’impulsion x’y’. Dans le référentiel x’y’, en translation par rapport au précédent à la vitesse v, l’impulsion, est au repos et la position du déplacement vertical est donnée en fonction de x’.
y=f(x’) (1)
Dans le référentiel xy, la perturbation se déplace à la vitesse v, la fonction déterminant la position verticale du déplacement est donc fonction du temps et de x, soit
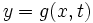 (2)
(2)Pour relier les coordonnées (1) et (2) on utilise les transformations de Galilée, qui sont un groupe de transformations utilisées pour lier deux systèmes de coordonnées en mouvement relatif rectiligne uniforme (pour des vitesses relativistes, il faut leur substituer les transformations de Lorentz, ce n’est pas nécessaire dans notre cas).
t’= t
x’= x-vt (3)
y’= yOn obtient donc
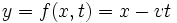 (4)
(4)qui détermine le déplacement d’une onde vers les x positifs et
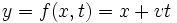 vers les x négatifs.
vers les x négatifs.Pour modéliser une onde sinusoïdale en fonction du temps, on pose d’abord
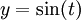 (5)
(5)On la recadre ensuite pour obtenir une amplitude entre a et b, centrée en 0 (la fonction sinus oscille entre -1 et 1), donc avec b=-a.
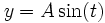 (6).
(6).La fonction sinus a une période de 2π, l’onde à une période T, en utilisant le nombre
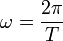 , lorsque t est un multiple de T, w est un multiple de 2π.
, lorsque t est un multiple de T, w est un multiple de 2π.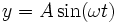 (7)
(7)De même, une fonction sinusoïdale l’est par rapport aux x. Comme pour (6),
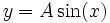 (8)
(8)Comme pour (7), il faut introduire le nombre d’onde
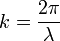 , où λ est la longueur d’onde, ainsi
, où λ est la longueur d’onde, ainsi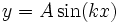 (9)
(9)Pour une période T, l’onde avance d’une longueur λ, ainsi,
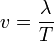 or
or 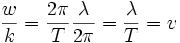 donc
donc 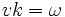 (10).
(10).Avec (4) et (8), on obtient l’équation d’onde générale
![y=A\sin[k(x-vt)]\,](/pictures/frwiki/53/596509e63273a812149468ddacfc0ac8.png)
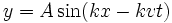 (11)
(11)
Avec (11) et (12) on a
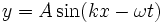 (13)
(13)
(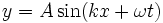 vers les x négatifs).
vers les x négatifs).
Cette relation vaut pour y=0 quand x=0 et t=0, ce qui n’est pas toujours le cas, il faut donc rajouter une phase à l’origine φ, donc
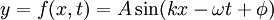
Application
L'image ci-dessous présente une utilisation de cette formule avec les données suivantes :
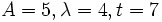 et
et 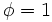
- Portail de la physique
Catégorie : Mécanique ondulatoire
Wikimedia Foundation. 2010.