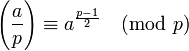Critere d'Euler

En mathématiques et plus précisément en arithmétique modulaire, le critère d'Euler est utilisé en théorie des nombres pour déterminer si un entier donné est un résidu quadratique modulo un nombre premier.

Définition

Considérons un nombre premier impair p et un entier a premier avec p ; alors le critère d'Euler s'énonce de la façon suivante :

1. si a est un résidu quadratique modulo p (c'est-à-dire s'il existe un entier k tel que k² ≡ a (mod p)), alors
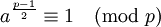
2. si a n'est pas un résidu quadratique modulo p alors .

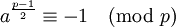ce qui s'écrit également, en utilisant le symbole de Legendre, de la façon suivante :

Démonstration du critère d'Euler

D'une part, nous considérons que a est un résidu quadratique modulo p. Nous trouvons k tel que k² ≡ a (mod p). Alors a^{(p − 1)/2} = k^{p − 1} ≡ 1 (mod p) par le petit théorème de Fermat.

D'autre part, nous considérons que a^{(p − 1)/2} ≡ 1 (mod p). Alors, soit α un élément primitif modulo p, autrement dit a = αⁱ. Donc, α^{i(p − 1)/2} ≡ 1 (mod p). Par le petit théorème de Fermat, (p − 1) divise i(p − 1)/2, donc i doit être pair. Soit k ≡ α^i/2 (mod p). Nous avons finalement k² = αⁱ ≡ a (mod p).

Exemples

Exemple 1 : Trouver les nombres premiers pour lesquels a est un résidu

Soit a = 17. Pour quels nombres premiers p, 17 est-il un résidu quadratique ?

Nous pouvons tester les nombres premiers p' donnés manuellement par la formule précédente.

Dans un cas, testons p = 3, nous avons 17^{(3 − 1)/2} = 17¹ ≡ 2 (mod 3) ≡ -1 (mod 3), par conséquent 17 n'est pas un résidu quadratique modulo 3.

Dans un autre cas, testons p = 13, nous avons 17^{(13 − 1)/2} = 17⁶ ≡ 1 (mod 13), par conséquent 17 est un résidu quadratique modulo 13. Comme confirmation, 17 ≡ 4 (mod 13) et 2² = 4.

Nous pouvons faire ces calculs plus rapidement en utilisant l'arithmétique modulaire et les propriétés du symbole de Legendre.

Si nous calculons les valeurs, nous trouvons :

(17/p) = +1 pour p = {13, 19, ...} (17 est un résidu quadratique modulo ces valeurs)

(17/p) = −1 pour p = {3, 5, 7, 11, 23, ...} (17 n'est pas un résidu quadratique modulo ces valeurs)

Exemple 2 : Trouver les résidus avec un module premier p donné.

Quels nombres sont les carrés modulo 17 (résidus quadratiques modulo 17) ?

Nous pouvons calculer manuellement :

1² = 1

2² = 4

3² = 9

4² = 16

5² = 25 ≡ 8 (mod 17)

6² = 36 ≡ 2 (mod 17)

7² = 49 ≡ 15 (mod 17)

8² = 64 ≡ 13 (mod 17)

Donc, l'ensemble des résidus quadratiques modulo 17 est {1,2,4,8,9,13,15,16}. Notez que nous n'avons pas besoin de calculer les carrés pour les valeurs de 9 à 16, comme elles sont toutes négatives par rapport à la valeurs carrée précédente (c.a.d. 9 ≡ −8 (mod 17), donc 9² = (−8)² = 64 ≡ 13 (mod 17)).

Nous pouvons trouver les résidus quadratique ou les vérifier en utilisant la formule précédente. Pour tester si 2 est un résidu quadratique modulo 17, nous calculons 2^{(17 − 1)/2} = 2⁸ ≡ 1 (mod 17), donc elle est un résidu quadratique. Pour tester si 3 est un résidu quadratique modulo 17, nous calculons 3^{(17 − 1)/2} = 3⁸ = 16 ≡ -1 (mod 17) donc, il n'est pas un résidu quadratique.

Le critère d'Euler est relié à la loi de réciprocité quadratique et est utilisé dans la définition des nombres pseudo-premiers d'Euler-Jacobi.

• Portail des mathématiques