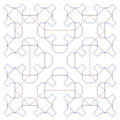
Courbe de Peano

Courbe de Peano
Giuseppe Peano

Une courbe de Peano est une courbe plane paramétrée par une fonction continue sur l'intervalle unité [0, 1], surjective dans le carré [0, 1]×[0, 1], c'est-à-dire que la courbe passe par chaque point du carré : elle « remplit l'espace ». Toutes ces courbes sont des fractales : bien que formées d'une simple ligne, elles sont de dimension 2. Ce type de courbes est nommé en l'honneur de Giuseppe Peano, qui fut le premier à en décrire une.

Sommaire

Historique

Dans un article de 1890[1] Giuseppe Peano décrit une courbe auto-intersectante qui passe par tous les points de la surface du carré unité. Son objectif est de construire une application de l'intervalle unité défini sur \scriptstyle{\R} vers le carré unité défini sur \scriptstyle{\R^2}. Il illustre ainsi un résultat de Georg Cantor qui, en 1877, établit que l'ensemble des points de l'intervalle unité et celui d'une surface bidimensionnelle finie avaient le même cardinal. Peano apporta la preuve qu'une telle fonction pouvait être continue. C'est-à-dire qu'une courbe pouvait remplir une surface.

La clé passe par l'élaboration d'une courbe nulle part différentiable. Toutes les courbes rencontrées jusqu'alors étaient différentiables par parties (elles avaient une dérivée continue sur chaque intervalle). En 1872, Karl Weierstrass avait bien décrit une fonction qui était continue en tout point mais différentiable en aucun point. Mais aucune de ces courbes ne pouvait remplir le carré unité. La courbe de Peano, à la fois nulle part différentiable et remplissant le plan, était donc fortement contre-intuitive.

Peano utilise l'existence d'un développement en base trois pour tout nombre réel. Dans l'ensemble des suites à valeurs dans {0,1,2}, il construit une correspondance entre la suite T =(a_n)_{n\in\N^*} et le couple de suites (X, Y)=((b_n)_{n\in\N^*}, (c_n)_{n\in\N^*}) de la manière suivante :

  • bn = a2n − 1 ou 2 − a2n − 1 selon que la somme des termes de rang pair de la suite (an) : \sum_{1\le k\le n-1}a_{2k} est paire ou impaire (par convention, la somme vide \sum_{1\le k\le0}a_{2k} est nulle donc paire, donc b1 = a1)
  • cn = a2n ou 2 − a2n selon que la somme des termes de rang impair de la suite (an) : \sum_{k=1}^{n}a_{2k-1} est paire ou impaire.
Quatre itérations de la courbe de Peano

À chaque suite, il associe le réel dont la suite est un développement en base 3

t=0,a_1a_2\cdots a_n\cdots = \sum_{k=1}^{+ \infty}a_k3^{-k},\qquad x=0,b_1b_2\cdots b_n\cdots = \sum_{k=1}^{+ \infty}b_k3^{-k},\qquad y=0,c_1c_2\cdots c_n\cdots = \sum_{k=1}^{+ \infty}c_k3^{-k}

et démontre que la correspondance qui, au réel t, associe le couple de réels (x,y) est bien une surjection continue de [0,1] dans [0,1]×[0,1].

L'article de Peano ne contenait pas d'illustration. Une observation des suites T, nulles à partir du rang 3, conduirait à la construction successive des points de coordonnées (0,0), (0,1/3), (0,2/3), (1/3,2/3), (1/3,1/3), (1/3,0), (2/3,0), (2/3,1/3), (2/3,2/3) qui, joints par des segments de droites donnent une courbe analogue à l'étape 1 de l'illustration ci-contre. Pour les suites nulles à partir du rang cinq, on trace une courbe analogue à l'itération 2 ci-contre, commençant au point de coordonnées (0,0) et aboutissant au point de coordonnées (8/9,8/9).

Un an plus tard, David Hilbert publie une construction nouvelle et plus simple, connue aujourd'hui sous le nom de courbe de Hilbert. Son article de 1891[2] est le premier à proposer une illustration de sa construction.

La plupart des courbes de Peano sont construites selon un procédé itératif et sont la limite d'une suite de courbes linéaires définies par parties.

À partir de l'exemple de Peano et de Hilbert, d'autres courbes continues sont conçues, ouvertes ou fermées :

  • en 1900, le mathématicien Eliakim Hastings Moore propose, en accolant quatre courbes de Hilbert, une variante fermée appelée aujourd'hui courbe de Moore (en) ;
  • en 1905, Henri Lebesgue propose une nouvelle courbe qui, elle, est différentiable en presque tout point ;
  • en 1912, le mathématicien polonais Wacław Sierpiński à son tour décrit une autre courbe fermée (en) qui porte désormais son nom.

Plus tard Walter Wunderlich (de) développe, quant à lui, une famille entière de variantes de la courbe originelle de Peano.

Propriétés

  • Une courbe de Peano n'est pas injective. La courbe est nécessairement auto-intersectante.
  • La courbe de Peano est 1/2-höldérienne. Néanmoins, il est impossible d'obtenir une application a-höldérienne surjective de [0,1] sur [0,1]2 pour a>1/2. Une preuve est mentionnée dans l'article Condition de Hölder.

Citation

« J'ai la plus grande estime pour M. Peano, qui a fait de très jolies choses (par exemple sa courbe qui remplit toute une aire), mais enfin, il n'est allé ni plus loin, ni plus haut, ni plus vite que la plupart des mathématiciens aptères et il aurait pu faire tout aussi bien avec ses jambes » (Henri Poincaré, Science et Méthode).

Références

  1. ↑ G. Peano, « Sur une courbe, qui remplit une aire plane », dans Math. Ann., vol. 36, 1890, p. 157-160 [texte intégral] 
  2. ↑ (de) D. Hilbert, « Über die stetige Abbildung einer Linie auf ein Flächenstück », dans Math. Ann., vol. 38, 1891, p. 459-460 [texte intégral] 

Voir aussi

Sur les autres projets Wikimedia :

Article connexe

Liste de fractales par dimension de Hausdorff

Liens externes

ẲẲ


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Courbe de Peano de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Courbe De Peano — Quatre itérations de la courbe de Peano Une courbe de Peano est une fonction continue sur l intervalle [0, 1], surjective dans le carré [0, 1] x [0, 1], c est à dire que la courbe passe par chaque point du carré. Elle est une fractale : bien …   Wikipédia en Français

  • Courbe de Péano — Courbe de Peano Quatre itérations de la courbe de Peano Une courbe de Peano est une fonction continue sur l intervalle [0, 1], surjective dans le carré [0, 1] x [0, 1], c est à dire que la courbe passe par chaque point du carré. Elle est une… …   Wikipédia en Français

  • Courbe de peano — Quatre itérations de la courbe de Peano Une courbe de Peano est une fonction continue sur l intervalle [0, 1], surjective dans le carré [0, 1] x [0, 1], c est à dire que la courbe passe par chaque point du carré. Elle est une fractale : bien …   Wikipédia en Français

  • courbe de Peano — ● courbe de Peano Arc paramétré (I, f), où f est une application continue de I = [0, 1] dans E2, plan affine, dont le support passe par tous les points d un carré. (C est un des premiers exemples de fractale.) …   Encyclopédie Universelle

  • PEANO (G.) — Le mathématicien italien Peano s’est principalement intéressé aux fondements des mathématiques, ainsi qu’à la théorie des langages. Grâce à lui, on comprendra mieux aujourd’hui la fécondité des méthodes formelles et axiomatiques. L’actualité de… …   Encyclopédie Universelle

  • Courbe Plane — En géométrie, une courbe plane est une courbe qui est entièrement contenue dans un (unique) plan, et qui est identifiable à une fonction continue : où I est un intervalle de l ensemble des nombres réels. L image d une courbe est aussi… …   Wikipédia en Français

  • Courbe de Gosper — à la 4ème itération La Courbe de Gosper, baptisée d après son découvreur Bill Gosper, est une courbe de Peano remplissant le plan. Il s agit d une courbe fractale, voisine, dans sa construction, à la courbe du dragon ou la courbe de Hilbert …   Wikipédia en Français

  • Courbe rectifiable — Longueur d un arc Camille Jordan est l auteur de la définition la plus courante de la longueur d un arc. En géométrie, la question de la longueur d un arc est intuitivement simple à concevoir. L idée d arc correspond à celle d une ligne, ou d une …   Wikipédia en Français

  • Courbe — En géométrie, le mot courbe, ou ligne courbe désigne certains sous ensembles du plan, de l espace usuels. Par exemple, les droites, les segments, les lignes polygonales et les cercles sont des courbes. La notion générale de courbe se décline en… …   Wikipédia en Français

  • Peano — Giuseppe Peano Giuseppe Peano Giuseppe Peano (Spinetta di Cuneo (Coni), 27 août 1858 Turin, 20 avril 1932) est un mathématicien italien de la fin du XIXe et du début du …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”