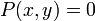Conjecture de Mordell

Conjecture de Mordell

Théorème de Faltings

En théorie des nombres, le théorème de Faltings, précédemment connu sous le nom de conjecture de Mordell donne des résultats sur le nombre de solutions d'une équation diophantienne. Il a été conjecturé par le mathématicien anglais Louis Mordell et démontré par Gerd Faltings en 1983, soit environ soixante ans après que la conjecture fut posée.

Énoncé

Soit l'équation définie de la manière suivante :

P(x,y) = 0\,

Avec P un polynôme à coefficients rationnels. Le problème est de trouver le nombre de solutions X de cette équation dans l'ensemble des rationnels.

Le nombre de solution dépend du genre de la courbe C associée à cette équation (on peut définir empiriquement le genre d'une courbe comme le nombre de fois où il est possible de couper cette courbe sans obtenir 2 morceaux distincts).

  • Si le genre vaut 0 (par exemple une droite), alors :
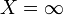    • Soit X = \infty ;
    • Soit X = 0.
  • Si le genre vaut 1, alors :
  • Si le genre est supérieur ou égal à 2, Mordell avait conjecturé qu'il n'y avait qu'un nombre fini de points. Ceci fut effectivement démontré par Gerd Faltings en 1983.

Application

Équation de Fermat

Soit l'équation :

xn + yn = zn

dont on cherche les solutions entières. Si (a,b,c) est une solution avec c non-nul, alors (a / c,b / c) est une solution à cordonnées rationnelles de l'équation

un + vn = 1.

Elle correspond à une courbe de genre 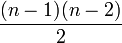\frac{(n-1)(n-2)}{2}. Ainsi, pour n supérieur ou égal à 4, elle est de genre supérieur ou égal à 2, et n'admet donc qu'un nombre fini de solutions rationnelles. On sait borner le nombre de solutions, mais pas encore leur taille. Cette approche pour démontrer le Grand théorème de Fermat, alternative à celle suivie par Andrew Wiles, n'a donc pas encore abouti.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Faltings ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Conjecture de Mordell de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Conjecture De Birch Et Swinnerton-Dyer — Pour les articles homonymes, voir BSD (homonymie). En mathématiques, la conjecture de Birch et Swinnerton Dyer (BSD) relie le rang du groupe abélien de points sur un corps de nombres d une courbe elliptique E à l ordre du zéro de la fonction L… …   Wikipédia en Français

  • Conjecture de birch et swinnerton-dyer — Pour les articles homonymes, voir BSD (homonymie). En mathématiques, la conjecture de Birch et Swinnerton Dyer (BSD) relie le rang du groupe abélien de points sur un corps de nombres d une courbe elliptique E à l ordre du zéro de la fonction L… …   Wikipédia en Français

  • Conjecture Abc — La conjecture abc est une conjecture en théorie des nombres. Elle a été formulée pour la première fois par Joseph Oesterlé et David Masser en 1985. Si elle était vérifiée, elle permettrait de démontrer aisément le théorème de Fermat Wiles, entre… …   Wikipédia en Français

  • Mordell-Vermutung — Die Vermutung von Mordell entstammt der Zahlentheorie, wurde im Jahr 1922 von Louis Mordell aufgestellt und 1983 von Gerd Faltings in seinem Artikel Endlichkeitssätze für abelsche Varietäten über Zahlkörpern[1] (Faltings Satz) bewiesen.… …   Deutsch Wikipedia

  • Conjecture abc — La conjecture abc est une conjecture en théorie des nombres. Elle a été formulée pour la première fois par Joseph Oesterlé et David Masser en 1985. C est « le problème non résolu le plus important en analyse diophantienne[1] » car si… …   Wikipédia en Français

  • Conjecture de Birch et Swinnerton-Dyer — Pour les articles homonymes, voir BSD (homonymie). En mathématiques, la conjecture de Birch (en) et Swinnerton Dyer prédit que pour toute courbe elliptique sur le corps des rationnels, l ordre d annulation en 1 de la fonc …   Wikipédia en Français

  • Mordell–Weil theorem — In mathematics, the Mordell–Weil theorem states that for an abelian variety A over a number field K, the group A(K) of K rational points of A is a finitely generated abelian group, called the Mordell Weil group. The case with A an elliptic curve… …   Wikipedia

  • Mordell curve — y2 = x3 + 1, with solutions at ( 1, 0), (0, 1) and (0, 1) In algebra, a Mordell curve is an elliptic curve of the form y2 = x3 + n, where n is an integer and where n ≠ 0 …   Wikipedia

  • Louis Mordell — Louis Joel Mordell est un mathématicien américano britannique, né le 28 janvier 1888 à Philadelphie et mort le 12 mars 1972 à Cambridge. Pionnier par ses recherches en théorie des nombres, il est un spécialiste reconnu des équations… …   Wikipédia en Français

  • Vermutung von Mordell — Die Vermutung von Mordell entstammt der Zahlentheorie, wurde im Jahr 1922 von Louis Mordell aufgestellt und 1983 von Gerd Faltings in seinem Artikel Endlichkeitssätze für abelsche Varietäten über Zahlkörpern[1] (Faltings Satz) bewiesen.… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”