Complexe de chaines

Complexe de chaines

Homologie et cohomologie

Page d'aide sur l'homonymie Pour les articles homonymes, voir Homologie.

L'homologie est une technique générale en mathématiques qui sert à mesurer l'obstruction qu'ont certaines suites de morphismes à être exactes. Elle intervient dans de nombreux domaines comme l'algèbre, la topologie algébrique, la géométrie algébrique ou la géométrie différentielle.

Sommaire

Généralités

Complexe de chaines

Un complexe de chaines est la donnée d'une suite de groupes abéliens ou plus généralement d'objets d'une catégorie abélienne Mi et d'une famille d'homomorphismes, appelés opérateurs de bord 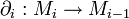\partial_i:M_i\rightarrow M_{i-1}, telle que : 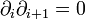\partial_i\partial_{i+1}=0 . Les éléments de Mi s'appellent des chaines de degré i. Les éléments du noyau 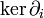\ker \partial_i s'appellent des cycles. Les éléments de l'image 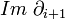Im\ \partial_{i+1} s'appellent des bords. Tout bord est un cycle. 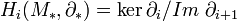Les groupes d'homologie du complexe M * sont alors, par définition : H_i(M_*,\partial_*)= \ker \partial_i / Im\ \partial_{i+1}.

Complexe de cochaines

Un complexe de cochaines est la donnée d'une suite de groupes abéliens ou plus généralement d'objets d'une catégorie abélienne Mi et d'une famille d'homomorphismes, appelés opérateurs de cobord 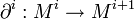\partial^i:M^i\rightarrow M^{i+1}, telle que : 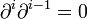\partial^i\partial^{i-1}=0 . Les éléments de Mi s'appellent des cochaines de degré i. Les éléments du noyau 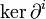\ker \partial^i s'appellent des cocycles. Les éléments de l'image 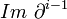Im\ \partial^{i-1} s'appellent des cobords. Tout cobord est un cocycle. 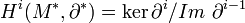Les groupes de cohomologie du complexe M * sont alors, par définition : H^i(M^*,\partial^*)= \ker \partial^i / Im\ \partial^{i-1}.

On remarque que si M * est un complexe de cochaines, on obtient un complexe de chaines en posant Mi = M − i. Cependant les deux terminologies existent car il peut être désagréable de modifier l'indexation.

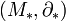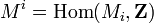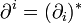Par exemple, si (M_*,\partial _*) est un complexe de chaines de groupes abéliens, posons M^i=\mathrm{Hom}(M_i,\mathbf{Z}) et \partial^i=(\partial_i)^* (l'application transposée). Alors 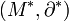(M^*,\partial^*) est un complexe de cochaines.

Exemple

À tout espace topologique, on peut associer son complexe de chaines singulières et donc son homologie singulière. Du point de vue de la théorie des catégories, l'homologie peut être vue comme un foncteur de la catégorie des espaces topologiques vers la catégorie des groupes abéliens gradués.

On peut remplacer les groupes abéliens par des modules sur un anneau commutatif.

Catalogue

Chaque théorie homologique mérite à elle seule un article. La liste suivante n'est pas exhaustive.

Bibliographie

Ouvrages de mathématiques

  • William Fulton ; Algebraic Topology: A First Course, Graduate Texts in Mathematics 153, Springer-Verlag (1995), ISBN 0-387-94327-7.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Homologie et cohomologie#Complexe de chaines ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Complexe de chaines de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Complexe de cochaines — Homologie et cohomologie Pour les articles homonymes, voir Homologie. L homologie est une technique générale en mathématiques qui sert à mesurer l obstruction qu ont certaines suites de morphismes à être exactes. Elle intervient dans de nombreux… …   Wikipédia en Français

  • Complexe différentiel — Pour les articles homonymes, voir Complexe et Différentielle. En mathématiques, un complexe différentiel est un groupe abélien (voire un espace vectoriel), ou plus généralement un objet d une catégorie abélienne, muni d un endomorphisme appelée… …   Wikipédia en Français

  • CHAÎNES (géomorphologie) — Les géomorphologues appellent chaîne une unité montagneuse complexe, caractérisée par un relief élevé, à fortes dénivellations, et, surtout, par la disposition ordonnée de ses éléments et de leurs combinaisons, selon une direction privilégiée qui …   Encyclopédie Universelle

  • CHAÎNES DE MONTAGNES (typologie) — À la surface de la Terre, les zones de relief élevé qui forment ce que l’on appelle des « chaînes de montagnes» constituent un trait morphologique de première importance, comparable à celui des dorsales qui sillonnent le fond des océans. Les… …   Encyclopédie Universelle

  • Complexe Antigène-anticorps — Complexe immun Les glomérulonéphrites, exemples classiques de maladies à complexes immuns Un complexe immun (ou complexe antigène anticorps) résulte de la combinaison d un épitope immunogène avec un anticorps dirigé spécifiquement contre cet… …   Wikipédia en Français

  • Complexe antigene-anticorps — Complexe immun Les glomérulonéphrites, exemples classiques de maladies à complexes immuns Un complexe immun (ou complexe antigène anticorps) résulte de la combinaison d un épitope immunogène avec un anticorps dirigé spécifiquement contre cet… …   Wikipédia en Français

  • Complexe antigène-anticorps — Complexe immun Les glomérulonéphrites, exemples classiques de maladies à complexes immuns Un complexe immun (ou complexe antigène anticorps) résulte de la combinaison d un épitope immunogène avec un anticorps dirigé spécifiquement contre cet… …   Wikipédia en Français

  • Complexe Convectif De Méso-échelle — CCM dans le sud du Minnesota le 19 juillet 2006 à 1332 TU Un Complexe convectif de méso échelle (CCM) est un ensemble orageux se formant généralement en fin de journée à partir d orages dispersés et qui atteint son apogée durant la nuit …   Wikipédia en Français

  • Complexe convectif de meso-echelle — Complexe convectif de méso échelle CCM dans le sud du Minnesota le 19 juillet 2006 à 1332 TU Un Complexe convectif de méso échelle (CCM) est un ensemble orageux se formant généralement en fin de journée à partir d orages dispersés et… …   Wikipédia en Français

  • Complexe convectif de mésoéchelle — Complexe convectif de méso échelle CCM dans le sud du Minnesota le 19 juillet 2006 à 1332 TU Un Complexe convectif de méso échelle (CCM) est un ensemble orageux se formant généralement en fin de journée à partir d orages dispersés et… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”