Homologie Des Groupes

Homologie Des Groupes

Homologie des groupes

Page d'aide sur l'homonymie Pour les articles homonymes, voir Homologie.

En algèbre homologique, l'homologie d'un groupe G est un invariant attaché à un groupe G.

Pour un groupe G, on note \mathbf{Z}[G], l'anneau dont le groupe abélien sous-jacent est le groupe abélien libre engendré par G et dont les produits sont donnés sur les éléments de base par les produits de G.

Plus précisément, un élément de \mathbf{Z}[G] est un objet de la forme :

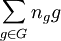
\sum_{g\in G} n_g g

où les ng sont presque tous nuls. Et le produit de deux tels éléments sont donnés par :


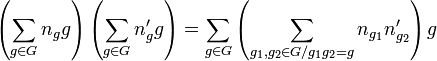
\left(\sum_{g\in G} n_g g\right)\left( \sum_{g\in G} n'_g g\right)=\sum_{g\in G}\left(\sum_{g_1,g_2\in G/g_1g_2=g} n_{g_1}n'_{g_2}\right) g


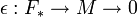Soit G un groupe, M un \mathbf{Z}[G]-module, c'est à dire un groupe abélien muni d'un homomorphisme de G dans le groupe des automorphismes de M. et \epsilon:F_*\rightarrow M\rightarrow 0 une résolution projective de M sur \mathbf{Z}[G].

Les groupes d'homologie de G à coefficients dans M sont définis par :

H_i(G;M)=H_i(F_*\otimes_{\mathbf{Z}[G]}\mathbf{Z})


De façon duale les groupes de cohomologie de G à coefficients dans M sont définis par :

H^i(G;M)=H^i(\mathrm{Hom}_{\mathbf{Z}[G]}(F_*,\mathbf{Z}))

Un résultat standard d'algèbre homologique montre que ces constructions sont indépendantes de la résolution F * choisie.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Homologie des groupes ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Homologie Des Groupes de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Homologie des groupes — Pour les articles homonymes, voir Homologie. En algèbre homologique, l homologie d un groupe est un invariant attaché à ce groupe. Pour un groupe G, on note l algèbre du groupe G, c est à dire l anneau dont le groupe abélien sous jacent est le… …   Wikipédia en Français

  • Homologie Singulière — Pour les articles homonymes, voir Homologie. En topologie algébrique, l homologie singulière est une construction qui permet d associer à un espace topologique X une suite homologique de groupes abéliens libres ou de modules. Cette association… …   Wikipédia en Français

  • Homologie singuliere — Homologie singulière Pour les articles homonymes, voir Homologie. En topologie algébrique, l homologie singulière est une construction qui permet d associer à un espace topologique X une suite homologique de groupes abéliens libres ou de modules …   Wikipédia en Français

  • Homologie Et Cohomologie — Pour les articles homonymes, voir Homologie. L homologie est une technique générale en mathématiques qui sert à mesurer l obstruction qu ont certaines suites de morphismes à être exactes. Elle intervient dans de nombreux domaines comme l algèbre …   Wikipédia en Français

  • Liste Des Groupes D'homologie — Le tableau suivant donne la liste des groupes d homologie pour les espaces topologiques usuels, avec comme coefficients, les entiers, les entiers modulo 2, ou les reels. Nom de l espace topologique Groupes d homologie à coefficients entiers… …   Wikipédia en Français

  • Homologie (géométrie) — Homologie (transformation géométrique) Pour les articles homonymes, voir Homologie. Homologie Il n existe apparemment aucun rapport entre les homologies géométriques vues dans cet article, et les groupes d homologie e …   Wikipédia en Français

  • Homologie (transformation geometrique) — Homologie (transformation géométrique) Pour les articles homonymes, voir Homologie. Homologie Il n existe apparemment aucun rapport entre les homologies géométriques vues dans cet article, et les groupes d homologie e …   Wikipédia en Français

  • Liste des groupes d'homologie — Le tableau suivant donne la liste des groupes d homologie pour les espaces topologiques usuels, avec comme coefficients, les entiers, les entiers modulo 2, ou les reels. Nom de l espace topologique Groupes d homologie à coefficients entiers… …   Wikipédia en Français

  • Cohomologie Des Groupes Profinis — La cohomologie des groupes profinis est une théorie cohomologique, reposant sur la théorie des groupes profinis. Elle consiste en un raffinement de la cohomologie des groupes classique, principalement par la prise en compte de la nature… …   Wikipédia en Français

  • Cohomologie des groupes profinis — La cohomologie des groupes profinis est une théorie cohomologique, reposant sur la théorie des groupes profinis. Elle consiste en un raffinement de la cohomologie des groupes classique, principalement par la prise en compte de la nature… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”