Homologie De Morse

Homologie de Morse

Pour les articles homonymes, voir Homologie.

L'homologie de Morse est une approche homologique de la théorie de Morse. Elle permet de comprendre l'homologie d'une variété différentielle compacte par la donnée d'une fonction de Morse et d'une métrique riemannienne (avec des conditions de compatibilité). Réciproquement, l'homologie de Morse permet de comprendre combinatoirement la dynamique d'un flot de gradient générique d'une fonction de Morse donnée sur une variété compacte à partir de l'homologie de la variété. Cette approche homologique conduit à l'écriture des inégalités de Morse.

Fixons une fonction de Morse f sur une variété différentielle compacte M, munie d'une métrique riemannienne g. En pratique, le choix de la métrique riemannienne g a une importance secondaire : l'espace des métriques riemanniennes est un cône convexe de l'espace des sections du fibré vectoriel $S²M \to M$ , et des variations globales sur g peuvent être effectuées.

L'homologie de Morse consiste à définir un complexe de chaînes ou de cochaînes suivant les auteurs, soit donc :

Un A-module gradué C_*(f,A) ou C^*(f,A), dont la définition est indépendante de g ;
Une application A-linéaire d:C_*(f,A)→C_*(f,A) ou d:C^*(f,A)→C^*(f,A), de carré nul, et de degré -1 ou +1.

Plus explicitement, C_*(f,A) ou C^*(f,A) est le A-module libre de base l'ensemble des points critiques de la fonction f ; la graduation dépend d'une convention. L'opérateur de bord ou de cobord d se définit en comptant les orbites du flot de plus ou moins le gradient de f connectant des points critiques présentant une différence d'indices de 1. La finitude du nombre de telles orbites est assurée par une condition générique portant sur f ou sur g. L'introduction de signes est nécessaire pour assurer que le carré de d soit nul.

Les groupes d'homologie ou de cohomologie du complexe de chaînes ou de cochaînes ainsi définis sont indépendants du choix de la métrique g : ils sont notés H_*(f,A) ou H^*(f,A). Ils sont naturellement isomorphes aux groupes d'homologie ou de cohomologie de la variété M à coefficients dans A.

Sommaire

1 Graduation
2 Condition de Morse-Palais
3 Espaces de module
4 Orientation
- 4.1 Opérateur de bord ou de cobord
5 Références
6 Liens internes

Graduation

La graduation du A-module C_*(f,A) ou C^*(f,A) dépend d'un choix d'indexation des points critiques de la fonction f.

En un point critique x de f, la matrice hessienne de f est bien définie et indépendante du choix de la métrique riemannienne. La non-dégénérescence de x signifie exactement que la hessienne H_x est une forme bilineaire non dégénérée sur T_xM. L'indice de M dépend de sa signature ; deux conventions coexistent :

L'indice $μ(x)$ est défini comme la dimension d'un sous-espace défini positif maximal ;
L'indice $ν(x)$ est défini comme la dimension d'un sous-espace défini négatif maximal.

Le A-module C_k(f,A) C^k(f,A) est le A-module libre de base l'ensemble des points critiques de f d'indice k.

Condition de Morse-Palais

Article détaillé : Condition de Morse-Palais.

A une métrique riemannienne g fixée est associé le champ de vecteurs gradient X de f defini par :

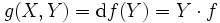$g(X,Y)=\mathrm df(Y)=Y\cdot f$ .

La condition de Morse-Palais (ou de Morse-Smale, ou de Palais-Smale, ou de Morse-Palais-Smale suivant les auteurs) est une condition générique au sens de Baire portant sur le choix de la fonction de Morse f ou le choix de la métrique riemannienne g. Elle s'énonce ainsi :

Les variétés stables et instables de X ou de -X aux points critiques de f s'intersectent deux à deux transversalement.

Par compacité, les champs X et -X sont globaux. Les solutions de l'équation différentielle :

$\frac{\mathrm d}{\mathrm dt}u(t)=\pm X\bigl[u(t)\bigr]$

sont globalement définies sur R, et admettent des limites en 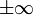$\pm\infty$ , limites qui sont des points critiques de f. La condition de Morse-Palais est suffisante pour définir l'opérateur de bord ou de cobord d.

Espaces de module

Pour deux points critiques x et y de f, on note 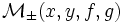$\mathcal{M}_{\pm}(x,y,f,g)$ l'espace des orbites du flot de ±X allant de x à y ; id est, l'espace des applications R 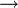$\rightarrow$ M vérifiant le problème aux limites :

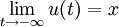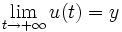$\frac{\mathrm d}{\mathrm dt}u(t)=\pm X\left[u(t)\right]$ ; $\lim_{t\rightarrow -\infty}u(t)=x$ et $\lim_{t\rightarrow +\infty}u(t)=y$ .

La topologie considérée est en général la topologie de convergence uniforme sur tout compact de R. L'écriture de l'homologie de Morse ne pose pas la question de l'existence de solutions à ce problème aux limites. Éventuellement, 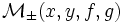$\mathcal{M}_{\pm}(x,y,f,g)$ peut être vide.

L'espace 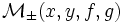$\mathcal{M}_{\pm}(x,y,f,g)$ est naturellement homéomorphe à l'intersection de la variété stable W_s(y, 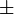$\pm$ X) en y et de la variété instable W_u(x, 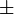$\pm$ X) en x (pour le champ 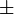$\pm$ X).

Sous la condition de Morse-Palais, cette intersection est une sous-variété différentielle de M dont la dimension s'exprime comme différence des indices des points critiques x et y :

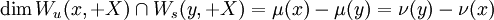$\dim W_u(x,+X)\cap W_s(y,+X)=\mu(x)-\mu(y)=\nu(y)-\nu(x)$ ;
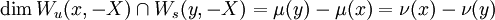$\dim W_u(x,-X)\cap W_s(y,-X)=\mu(y)-\mu(x)=\nu(x)-\nu(y)$ .

Conventionnellement, une variété de dimension strictement négative est vide.

Le groupe R agit continument sur 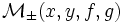$\mathcal{M}_{\pm}(x,y,f,g)$ et le quotient est une variété, notée 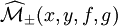$\widehat{\mathcal{M}}_{\pm}(x,y,f,g)$ dont la dimension est donnée par :

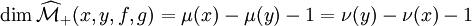$\dim \widehat{\mathcal{M}}_{+}(x,y,f,g)=\mu(x)-\mu(y)-1=\nu(y)-\nu(x)-1$ ;
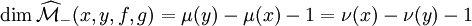$\dim \widehat{\mathcal{M}}_{-}(x,y,f,g)=\mu(y)-\mu(x)-1=\nu(x)-\nu(y)-1$ .

Orientation

Opérateur de bord ou de cobord

Suivant les coventions fixées, on définit un opérateur de bord ou de cobord ; le tableau suivant résume la situation :

	Index $μ$	Index $ν$
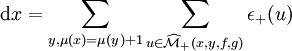
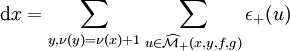
Champ X	Opérateur de bord $\mathrm dx=\sum_{y,\mu(x)=\mu(y)+1}\sum_{u\in\widehat{\mathcal{M}}_+(x,y,f,g)}\epsilon_+(u)$	Opérateur de cobord $\mathrm dx=\sum_{y,\nu(y)=\nu(x)+1}\sum_{u\in\widehat{\mathcal{M}}_+(x,y,f,g)}\epsilon_+(u)$
Champ -X	Opérateur de cobord 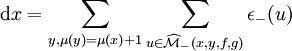$\mathrm dx=\sum_{y,\mu(y)=\mu(x)+1}\sum_{u\in\widehat{\mathcal{M}}_-(x,y,f,g)}\epsilon_-(u)$	Opérateur de bord 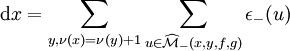$\mathrm dx=\sum_{y,\nu(x)=\nu(y)+1}\sum_{u\in\widehat{\mathcal{M}}_-(x,y,f,g)}\epsilon_-(u)$

Si A est un anneau de caractéristique 2, l'introduction des signes n'est pas nécessaire.

Références

Jürgen Jost, Riemannian Geometry and Geometric Analysis, Fourth Edition, Springer, 2005.

Liens internes

Portail des mathématiques

Ce document provient de « Homologie de Morse ».

Catégories : Théorie de Morse | Champ de vecteurs | Théorie d'homologie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Homologie De Morse de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Homologie de morse — Pour les articles homonymes, voir Homologie. L homologie de Morse est une approche homologique de la théorie de Morse. Elle permet de comprendre l homologie d une variété différentielle compacte par la donnée d une fonction de Morse et d une… … Wikipédia en Français
Homologie de Morse — Pour les articles homonymes, voir Homologie. L homologie de Morse est une approche homologique de la théorie de Morse. Elle permet de comprendre l homologie d une variété différentielle compacte par la donnée d une fonction de Morse et d une… … Wikipédia en Français
Homologie De Floer — Pour les articles homonymes, voir Homologie. L homologie de Floer est une adaptation de l homologie de Morse en dimension infinie. Sommaire 1 Homologie de Floer symplectique 2 … Wikipédia en Français
Homologie de floer — Pour les articles homonymes, voir Homologie. L homologie de Floer est une adaptation de l homologie de Morse en dimension infinie. Sommaire 1 Homologie de Floer symplectique 2 … Wikipédia en Français
Homologie Et Cohomologie — Pour les articles homonymes, voir Homologie. L homologie est une technique générale en mathématiques qui sert à mesurer l obstruction qu ont certaines suites de morphismes à être exactes. Elle intervient dans de nombreux domaines comme l algèbre … Wikipédia en Français
Homologie de Floer — Pour les articles homonymes, voir Homologie. L homologie de Floer est une adaptation de l homologie de Morse en dimension infinie. Sommaire 1 Homologie de Floer symplectique 2 Variétés compactes … Wikipédia en Français
Homologie et cohomologie — Pour les articles homonymes, voir Homologie. L homologie est une technique générale en mathématiques qui sert à mesurer l obstruction qu ont certaines suites de morphismes à être exactes. Elle intervient dans de nombreux domaines comme l algèbre … Wikipédia en Français
Homologie — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Homologie », sur le Wiktionnaire (dictionnaire universel) Le mot homologie est employé dans plusieurs… … Wikipédia en Français
Morse — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Un morse. Le morse est un mammifère marin, mais l appellation peu … Wikipédia en Français
Morse-Theorie — Die Morsetheorie aus dem Bereich der Differentialtopologie gibt einen sehr direkten Zugang zur Analyse der Topologie einer Mannigfaltigkeit über das Studium differenzierbarer Funktionen auf dieser Mannigfaltigkeit. Die wesentlichen Einsichten… … Deutsch Wikipedia

Dictionnaires et Encyclopédies sur 'Academic'

Homologie De Morse