Theoreme 90 de Hilbert
- Theoreme 90 de Hilbert
-
Théorème 90 de Hilbert
En théorie de Galois, le théorème 90 de Hilbert est une propriété algébrique d'énoncé simple, et de grande portée, de par son interprétation homologique.
Ce théorème tire son nom de l'ouvrage paru en 1897, Zahlbericht, par David Hilbert, dans lequel il est énoncé, et démontré, comme théorème 90. Il a été ensuite généralisé par Emmy Noether.
Considérant une extension cyclique de corps de nombres L/K, et g un générateur de son groupe de Galois G, ce théorème stipule que tout élément a de L de norme 1 est de la forme :
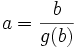
pour un certain élément b du corps L. Cette propriété traduit en fait très exactement l'annulation du premier groupe de cohomologie galoisienne 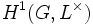 .
.
 Portail des mathématiques
Portail des mathématiques
Catégories : Théorème de mathématiques | Théorie de Galois
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme 90 de Hilbert de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Théorème 90 de hilbert — En théorie de Galois, le théorème 90 de Hilbert est une propriété algébrique d énoncé simple, et de grande portée, de par son interprétation homologique. Ce théorème tire son nom de l ouvrage paru en 1897, Zahlbericht, par David Hilbert, dans… … Wikipédia en Français
Théorème 90 de Hilbert — En théorie de Galois, le théorème 90 de Hilbert est une propriété algébrique d énoncé simple, et de grande portée, de par son interprétation homologique. Ce théorème tire son nom de l ouvrage paru en 1897, Zahlbericht, par David Hilbert, dans… … Wikipédia en Français
HILBERT (D.) — Le mathématicien allemand David Hilbert a ouvert la voie à plusieurs générations de chercheurs et a joué un rôle important dans l’élaboration des idées, non seulement dans sa spécialité, mais dans le cadre d’une réflexion générale sur la science … Encyclopédie Universelle
Hilbert — David Hilbert David Hilbert David Hilbert en 1912 Naissance 23 janvier 1862 Königsberg (Prusse Orientale) … Wikipédia en Français
Théorème d'Artin-Schreier — Théorie d Artin Schreier En mathématiques, la théorie d Artin Schreier donne une description des extensions galoisiennes de degré p d un corps de caractéristique p. Elle traite donc un cas inaccessible à la théorie de Kummer. Extension d Artin… … Wikipédia en Français
HILBERT (PROBLÈMES DE) — «Qui ne se réjouirait de pouvoir soulever le voile qui cache le futur, de jeter un regard sur le développement des mathématiques, ses progrès ultérieurs, les secrets des découvertes des siècles à venir?...» Prévoir le futur des mathématiques: qui … Encyclopédie Universelle
Theoreme d'incompletude de Godel — Théorème d incomplétude de Gödel Les théorèmes d incomplétude de Gödel sont deux théorèmes célèbres de logique mathématique, démontrés par Kurt Gödel en 1931 dans son article Über formal unentscheidbare Sätze der Principia Mathematica und… … Wikipédia en Français
Théorème d'incomplétude — de Gödel Les théorèmes d incomplétude de Gödel sont deux théorèmes célèbres de logique mathématique, démontrés par Kurt Gödel en 1931 dans son article Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme (Sur les… … Wikipédia en Français
Théorème d'incomplétude de Godel — Théorème d incomplétude de Gödel Les théorèmes d incomplétude de Gödel sont deux théorèmes célèbres de logique mathématique, démontrés par Kurt Gödel en 1931 dans son article Über formal unentscheidbare Sätze der Principia Mathematica und… … Wikipédia en Français
Théorème d'incomplétude de Gödel — Les théorèmes d incomplétude de Gödel sont deux théorèmes célèbres de logique mathématique, démontrés par Kurt Gödel en 1931 dans son article Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme (Sur les propositions … Wikipédia en Français
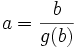
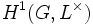 .
.