Cercles de Johnson

Cercles de Johnson et cercle circonscrit aux trois points d'intersection

En géométrie plane, les cercles de Johnson sont trois cercles de même rayon et ayant un point H en commun. Les trois autres points d'intersection des cercles entre eux possèdent de nombreuses propriétés.

Il se peut, dans le cas où deux des cercles sont tangents, qu'un des points soit confondu avec H mais, même dans ce cas particulier, les résultats énoncés ci-dessous restent valides.

Théorème de Johnson

Roger Johnson démontre vers 1916^[1] que ces trois points sont sur un cercle de même rayon que les trois premiers cercles.

Démonstration : une démonstration consiste à mettre en évidence une série de losanges.

Cercles de Johnson avec les trois losanges complétés par le point O qui donne l'illusion d'un dessin de cube en perspective

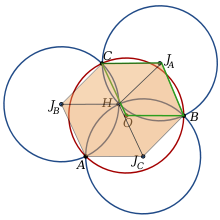
Si on appelle J_A, J_B, J_C les centres des trois cercles Γ_a, Γ_b, Γ_c de rayon r, H leur point de concours et A, B et C les points d'intersections respectifs de Γ_b etΓ_c, de Γ_c et Γ_a, de Γ_a et Γ_b, on observe la présence de trois losanges de côté r :

J_ACJ_BH, J_BHJ_CA, J_CHJ_AB.

On construit alors le point O tel que BJ_ACO soit un parallélogramme. Ce parallélogramme ayant deux côtés consécutifs de longueur r c'est un losange de côté r.

De plus, on obtient les égalités vectorielles suivantes :

.

Le quadrilatère AJ_BCO est donc un parallélogramme, ce parallélogramme possède deux côtés consécutifs de longueur r. C'est donc un losange de côté r.

On obtient ainsi les égalités

r = OA = OB = OC.

On prouve ainsi que les trois points sont sur un cercle de centre O et de rayon r.

Système orthocentrique

On peut d'autre part observer que le point H est orthocentre du triangle ABC.

En effet, dans les losanges définis précédemment, le vecteur est orthogonal à la droite (J_AJ_B). Or les égalités vectorielles précédentes permettent de dire que le quadrilatère BJ_AJ_BA est un parallélogramme. Le vecteur est donc aussi orthogonal à (AB).

Il en est de même du vecteur et de la droite (AC) ainsi que du vecteur et de la droite (BC). Le point H est bien orthocentre du triangle (ABC).

Triangle de Johnson

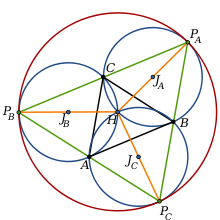
On appelle triangle de Johnson, le triangle formé par les centres des trois cercles. Ce triangle est le symétrique du triangle formé par les points d'intersection des trois cercles, par rapport au centre du cercle des neuf points commun aux deux triangles.

Cercles de Johnson et triangle anticomplémentaire

Démonstration : Si on appelle P_A, P_B, P_C, les points diamétralement opposés à H dans les cercles Γ_a, Γ_b, Γ_c, le point H est centre du cercle circonscrit au triangle P_AP_BP_C.

Puisque J_AHJ_BC est un parallélogramme, il en est de même de P_AJ_AJ_BC. Il y a donc égalité des vecteurs et . De même, les vecteurs et sont égaux. Le point C est donc milieu de P_AP_B. De même, le point B est milieu de P_CP_A et le point A est donc milieu de P_CP_B.

Le triangle P_AP_BP_C est l'image du triangle (ABC) par l'homothétie de centre G, l'isobarycentre du triangle, et de rapport -2. Le triangle J_AJ_BJ_C étant l'image du triangle P_AP_BP_C par l'homothétie de centre H et de rapport 1/2, il est aussi l'image de (ABC) par la composée de ces deux homothéties, c'est-à-dire par une homothétie de rapport -1 et de centre J, barycentre des points G et H affectés des coefficients -3/2 et -1/2. Or ce point correspond au centre du cercle des neuf points du triangle ABC. Par symétrie, c'est aussi le centre du cercle des neuf points du triangle de Johnson.

On peut remarquer en outre que les deux triangles ont même droite d'Euler qui, passant par J, reste globalement invariante par la symétrie de centre J et que les points O et H, centres respectifs des cercles circonscrits aux deux triangles sont également symétriques par rapport à ce point.

Note et référence

Lien externe

(en) Eric W. Weisstein, « Johnson's Theorem », MathWorld

• Portail de la géométrie