- Théorème japonais
-
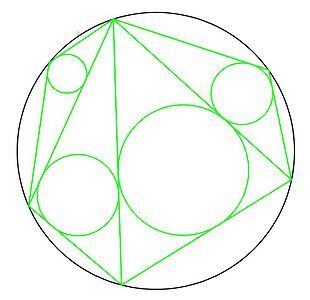
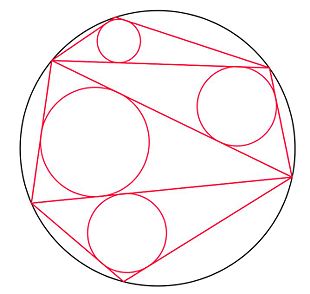
En géometrie, le théorème japonais dit que quelle que soit la manière dont on triangule un polygone inscriptible, la somme des rayons des cercles inscrits dans ces triangles est constante.
somme des rayons des cercles verts = somme des rayons des cercles rouges Sommaire
Propriétés mathématiques
Réciproquement, si la somme des rayons des cercles inscrits est constante quelle que soit la triangulation, alors le polygone est inscriptible. Le théorème japonais découle du théorème de Carnot.
Ce théorème est aussi une généralisation du théorème japonais pour les quadrilatères inscriptibles. Ce théorème montre que les centres des cercles inscrits dans les triangles issus des deux triangulations possibles d'un quadrilatère inscriptible forment un rectangle.
Le cas des quadrilatères suffit à prouver le cas général. En effet, en triangulant un polygone inscriptible, on crée plusieurs quadrilatères inscriptibles, et après application du théorème concernant les quadrilatères, chaque "changement de diagonale" créera une autre possibilité de triangulation. On peut ainsi créer toutes les triangulations possibles tout en conservant la somme des rayons des cercles inscrits dans tous les triangles formés et a fortiori dans le polygone tout entier. D'où le théorème pour les polygones inscriptibles, considéré ici peut être considéré comme un corollaire du théorème japonais pour les quadrilatères inscriptibles.
Histoire
Le nom de théorème japonais fait référence aux sangakus, ces figures géométriques illustrant une propriété mathématique et accrochées dans les temples japonais. D'après le professeur Yoshida de l'université de Kyoto[1], ce théorème est d'origine chinoise et porte, au Japon, le nom de théorème chinois. C'est le japonais Ryokan Maruyama qui en fait un Sangaku vers 1800. C'est ainsi que le théorème porte aussi le nom de théorème de Maruyama. Mais d'après le professeur Sato Naonobu de l'université d'Akita, il existe une preuve de ce théorème antérieure à 1800, œuvre du samurai Shinpei Ito[2]. Ce théorème est popularisé en Occident par Roger A. Johnson qui le nomme en 1929 théorème d'origine orientale[3], puis est nommé théorème japonais vers 1993.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Japanese theorem for cyclic polygons » (voir la liste des auteurs)
- Mango Ahura, Warau Uegaki, Kayo Matsushita, [ps]In search of "Japanese theorem
- (en) Sato Naonobu, Tateoka Jun, On the Old Mathematical Problems in Akita Prefecture
- Roger A. Johnson, Advanced euclidean geometry, 1929.
Voir aussi
Articles connexes
- Théorème de Carnot, qui est utilisé dans une preuve du théorème ci-dessus
Liens externes
Catégories :- Théorème de géométrie
- Cercle et sphère
Wikimedia Foundation. 2010.