- Mesure de Jordan
-
En mathématiques, la mesure de Peano-Jordan est une extension de la notion de taille ( longueur, aire ,volume ), aisément définie pour des domaines simples tels que le rectangle ou le parallélépipède, à des formes plus compliquées. La mesure de Jordan s'avère trop restrictive pour certains ensembles qu'on pourrait souhaiter être mesurables. Pour cette raison, il est maintenant plus fréquent de travailler avec la mesure de Lebesgue, qui est une extension de la mesure de Jordan à une plus grande classe d'ensembles. Historiquement, la mesure la Jordan, introduite vers la fin du XIXe siècle, est antérieure. La mesure de Peano-Jordan tire son nom de ses concepteurs, le mathématicien français Camille Jordan, et le mathématicien italien Giuseppe Peano [1].
Sommaire
La mesure de Jordan d'ensembles " simples"
Un ensemble simple est, par définition la réunion de rectangles (pouvant se chevaucher).
L'ensemble simple ci-dessus est recomposé en une union de rectangles sans chevauchements.Considérons l' espace euclidien Rn . On commence par considérer les produits d' intervalles bornés:
qui sont fermés à gauche et ouverts à droite. Un tel ensemble sera appelé un rectangle à n-dimensions , ou tout simplement un rectangle . On définit la mesure de Jordan d'un tel rectangle comme le produit de la longueur des intervalles:
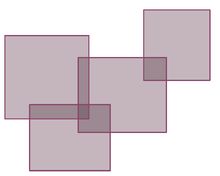
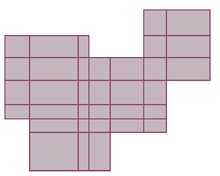
On considère ensuite des ensembles simples, parfois appelé polyrectangles, qui sont des unions de familles finies de rectangles:
pour tout k≥1. On ne peut pas définir la mesure de Jordan de S comme étant simplement la somme des mesures des rectangles individuels, car une telle représentation de S est loin d'être unique, et il pourrait y avoir des chevauchements importants entre les rectangles. Heureusement, tout ensemble simple S peut être recomposé comme l' union d'une autre famille finie de rectangles qui cette fois sont mutuellement disjoints. Puis on définit la mesure Jordan m(S) comme la somme des mesures des rectangles disjoints. On peut montrer que cette définition de la mesure de Jordan de S est indépendante de la représentation de S comme une union finie de rectangles disjoints.
Extension aux ensembles plus complexes
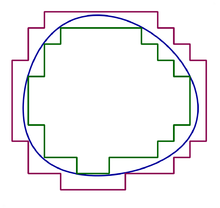
Un ensemble (représenté sur la figure par le domaine intérieur à la courbe bleue) est mesurable si et seulement si il peut être approximé à la fois par des ensembles simples intérieurs et extérieurs (leurs frontières figurent respectivement en vert foncé et en rose foncé).Soit un ensemble borné B . On définit sa mesure intérieure de Jordan comme:
et sa mesure extérieure comme:
où la borne supérieure (respectivement la borne supérieure) est relative aux mesures des ensembles simples S inclus dans B (respectivement dont B est une partie). L'ensemble B est dit mesurable (pour la mesure de Jordan) si sa mesure interne de B est égale à sa mesure externe. La valeur commune des deux mesures est alors simplement appelée la mesure de Jordan de B .
Propriétés
Tout rectangle (ouvert ou fermé), ainsi que toute boule et tout simplex est mesurable pour la mesure de Jordan. Si on considère deux fonctions continues, l'ensemble des points entre les graphes de ces fonctions est mesurable dés que cet ensemble est borné. Toute union finie et toute intersection d'ensembles mesurables est mesurable. Mais un ensemble compact n'est pas nécessairement mesurable. De même, l'ensemble des nombres rationnels contenus dans l'intervalle [0,1] n'est pas mesurable. Intuitivement cependant, l'ensemble des nombres rationnels est un "petit" ensemble, qui est dénombrable, dont on souhaiterait que la «taille» soit zéro. C'est vrai, mais seulement si l'on remplace la mesure de Jordan par la mesure de Lebesgue. La mesure de Lebesgue d'un ensemble est la même que sa mesure de Jordan lorsque cette dernière existe. Toutefois, la mesure de Lebesgue est définie pour une classe beaucoup plus large d'ensembles, comme l'ensemble des nombres rationnels dans un intervalle, et aussi pour des ensembles qui peuvent être non bornés ou pour des fractales. En outre, la mesure de Lebesgue, contrairement à la mesure de Jordan, est une vraie mesure, vérifiant la propriété d'additivité dénombrable: toute union dénombrable d'ensembles mesurables est mesurable.
Notes et références
- (en) Emmanuele DiBenedetto, Real analysis, Basel, Switzerland, Birkhäuser, 2002 (ISBN 0-8176-4231-5)
- (en) Richard Courant, Fritz John,, Introduction to Calculus and Analysis Volume II/1: Chapters 1 - 4 (Classics in Mathematics), Berlin, Springer, 1999 (ISBN 3-540-66569-2)
- G. Peano, "Applicazioni geometriche del calcolo infinitesimale", Fratelli Bocca, Torino, 1887.
liens externes
- (en) « Mesure de Jordan », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, 2001 (ISBN 978-155608010-4) [lire en ligne]
Wikimedia Foundation. 2010.
