Diffusion anomale

Diffusion anomale

En diffraction de rayons X, la diffusion anomale ou diffusion résonante est un phénomène qui apparaît lorsque l'énergie des rayons X incidents est proche d'une arête d'absorption d'un atome du cristal. Les photons incidents sont alors absorbés et provoquent une excitation électronique de l'atome. La diffusion anomale se reflète dans l'expression du facteur de diffusion atomique, qui devient complexe.

La diffusion anomale est un processus de diffusion inélastique, puisqu'il y a absorption du rayonnement incident. En cristallographie, seule la partie élastique de la diffusion anomale est utilisée : le rayonnement diffusé a la même longueur d'onde que le rayonnement incident. La partie inélastique de la diffusion anomale est utilisée en diffusion inélastique résonante de rayons X (en).

Sommaire

Facteur de diffusion atomique

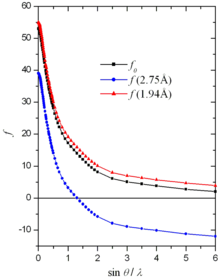Facteur de diffusion atomique de l'iode. En noir, f0 est le facteur de diffusion « normal ». Les courbes bleue et rouge sont la partie réelle du facteur de diffusion prenant en compte la diffusion anomale, pour 2,75 Å et 1,94 Å respectivement. Entre ces deux longueurs d'onde, l'iode possède trois arêtes d'absorption. Graphique effectué à partir des données publiées dans les tables internationales de cristallographie[1].
Dépendance en énergie de la partie réelle du facteur de diffusion atomique du chlore.
Article détaillé : Facteur de diffusion atomique.

Le facteur de diffusion atomique f est une mesure de la puissance de diffusion d'un atome. Il est une fonction continue du vecteur de diffusion[note 1]

\begin{array}{ll}\vec{K}=\vec{k}_f-\vec{k}_i, & \displaystyle{|\vec{k}_i|=|\vec{k}_f|=\frac{2\pi}{\lambda}}\end{array}

où \vec{k}_i et \vec{k}_f sont les vecteurs d'onde des faisceaux incident et diffusé, de même longueur d'onde λ mais de directions différentes.

Les premiers calculs du facteur de diffusion atomique furent effectués sous l'hypothèse de la diffusion Thomson et pour un atome de symétrie sphérique contenant Z électrons indépendants[2],[3],[4],[5],[6],[7]. Ce facteur de diffusion atomique « normal » f0 s'écrit alors comme la somme des facteurs de diffusion de chaque électron :

f_0(\vec{K}) = 4\pi \sum_{i=1}^Z \int_0^{\infty} \rho_i(r) \frac{\sin{Kr}}{Kr} r^2 \mbox{d}r

avec ρi(r) la densité électronique de l'électron i. Il en résulte que le facteur de diffusion atomique est une grandeur réelle.

Cette formule est bien adaptée pour les éléments à faible numéro atomique et pour la diffusion de rayons X à courtes longueurs d'onde. Cependant, elle ne prend pas en compte le fait que les électrons occupent des niveaux d'énergie discrets : lorsque les rayons X incidents ont une énergie proche d'une arête d'absorption de l'atome, ils provoquent une excitation des électrons, qui passent dans un niveau d'énergie supérieur et absorbent ainsi les photons. Cette diffusion anomale peut être prise en compte dans l'expression du facteur de diffusion atomique en ajoutant deux termes correctifs dépendant à la fois de la pulsation ω et du vecteur de diffusion, par analogie avec le système oscillant forcé amorti :

\begin{array}{ll}f(\omega,\vec{K}) = f_0(\vec{K}) + f'(\omega,\vec{K}) + if''(\omega,\vec{K}), & \displaystyle{\omega = \frac{2\pi c}{\lambda}=c|\vec{K}|}\end{array}

où f ' et f '' décrivent les variations en amplitude et en phase du facteur de diffusion par rapport à f0, c étant la vitesse de la lumière dans le vide. Ainsi, la diffusion anomale donne lieu à de la diffusion incohérente. Loin d'une arête d'absorption, ses effets sont négligeables.

La diffusion anomale a été prédite par Waller en 1928[8] ; sa prise en compte dans les calculs de facteur de diffusion atomique a suivi en 1993[9],[10].

Diffusion anomale et absorption

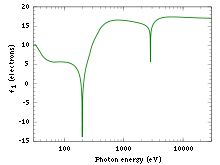
Les valeurs de f ' et f '' pour une longueur d'onde λ peuvent être déterminées expérimentalement en mesurant le coefficient d'absorption linéaire μ pour K = 0 (dans la direction du faisceau incident)[11],[12] :

\begin{array}{rcl} f'(\omega) & = & \displaystyle{\frac{2}{\pi} \int_0^{\infty} \frac{\omega ' f''(\omega ')}{\omega^2 - \omega '^2} \mbox{d}\omega '}\\[3ex] f''(\omega) & = & \displaystyle{\frac{mc\omega\sigma(\omega)}{4\pi e^2}} \end{array}

où σ est la section efficace d'absorption de l'atome, m la masse de l'électron et e sa charge électrique.

La connaissance des valeurs de f ' et f '' pour un atome permet de déterminer les énergies de liaison des électrons.

Les atomes de faible numéro atomique ne présentent pas de diffusion anomale aux longueurs d'onde utilisées en diffraction ; ils n'absorbent aussi quasiment pas les rayons X.

Applications

  • Lorsqu'un cristal présente de la diffusion anomale, il est possible de déterminer si son groupe ponctuel de symétrie est centrosymétrique : en effet, la loi de Friedel n'est dans ce cas plus vérifiée et les intensités des réflexions hkl et -h-k-l ne sont pas égales.
  • La méthode de la diffraction anomale est une méthode de solution du problème de phase[13] et est employée en synchrotron pour déterminer la structure de protéines et, plus généralement, de macromolécules. Elle nécessite la présence d'atomes avec un numéro atomique assez élevé dans la structure pour provoquer une diffusion anomale observable (à partir du soufre). En faisant varier la longueur d'onde des rayons X incidents près d'une arête d'absorption d'un élément lourd, le contraste entre les différents atomes change, ce qui permet de localiser les atomes lourds dans la maille.
  • La diffusion anomale est sensible aux déformations du nuage électronique des atomes. Cette particularité est exploitée dans la diffusion inélastique résonante de rayons X (en)[14].

Notes et références

Notes

  1. ↑ Le vecteur de diffusion \vec{K} est ici une variable continue. Il est parfois noté \vec{S} dans la littérature afin d'éviter la confusion avec le vecteur de diffraction, utilisé dans la théorie de la diffraction sur un cristal. Cette confusion ne peut pas être faite ici car seule la diffusion d'une onde par un atome isolé est traitée. L'ensemble des vecteurs de diffraction est un sous-ensemble discret de celui des vecteurs de diffusion ne contenant que les vecteurs satisfaisant la condition de Laue.

Références

  1. ↑ (en) International Tables for Crystallography, vol. C: Mathematical, physical and chemical tables, Dordrecht, Kluwer Academic Publishers, 1999, 2e éd. (1re éd. 1992) (ISBN 978-0-7923-5268-6) 
  2. ↑ (en) W.L. Bragg et J. West, dans Zeitschrift für Kristallographie, vol. 69, 1930, p. 118
  3. ↑ (en) D.R. Hartree, « The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part I. Theory and Methods », dans Mathematical Proceedings of the Cambridge Philosophical Society, vol. 24, no 1, 1928, p. 89-110 [lien DOI] 
  4. ↑ (en) D.R. Hartree, « The Wave Mechanics of an Atom with a non-Coulomb Central Field. Part III. Term Values and Intensities in Series in Optical Spectra », dans Mathematical Proceedings of the Cambridge Philosophical Society, vol. 24, no 3, 1928, p. 426-437 [lien DOI] 
  5. ↑ (en) D.R. Hartree, « The Distribution of Charge and Current in an Atom consisting of many Electrons obeying Dirac's equations », dans Mathematical Proceedings of the Cambridge Philosophical Society, vol. 25, no 2, 1929, p. 225-236 [lien DOI] 
  6. ↑ (en) L. Pauling, dans Proceedings of the Royal Society, vol. 114, 1927, p. 181
  7. ↑ (en) L. Pauling et I. Sherman, dans Zeitschrift für Kristallographie, vol. 81, 1932, p. 1
  8. ↑ (de) Ivar Waller, « Über eine verallgemeinerte Streuungsformel », dans Zeitschrift für Physik, vol. 51, no 3-4, 1928 [lien DOI] 
  9. ↑ (de) H. Hönl, « Zur Dispersionstheorie der Röntgenstrahlen », dans Zeitschrift für Physik, vol. 84, no 1-2, 1933, p. 1-16 [lien DOI] 
  10. ↑ (de) H. Hönl, « Atomfaktor für Röntgenstrahlen als Problem der Dispersionstheorie (K-Schale) », dans Annalen der Physik, vol. 410, no 6, 1933, p. 625-655 [lien DOI] 
  11. ↑ (en) R.W. James, The optical principles of the diffraction of X-rays, Cornell University Press, 1962, p. 135-192 
  12. ↑ (en) H. Wagenfeld, Theoretical computations of X-ray dispersion corrections. Anomalous scattering, S. Ramaseshan & S.C. Abrahams, 1975, p. 13-24 
  13. ↑ (en) J.M. Guss, E.A. Merritt, R.P. Phizackerley, B. Hedman, M. Murata, K.O. Hodgson et H.C. Freeman, « Phase determination by multiple-wavelength x-ray diffraction: crystal structure of a basic "blue" copper protein from cucumbers », dans Science, vol. 241, no 4867, 12 août 1988, p. 806-811 [lien DOI] 
  14. ↑ (en) Akio Kotani et Shik Shin, « Resonant inelastic x-ray scattering spectra for electrons in solids », dans Reviews of Modern Physics, vol. 73, no 1, 2001, p. 203-246 [lien DOI] 

Voir aussi

Liens externes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Diffusion anomale de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Diffusion — Modellhafte Darstellung der Durchmischung zweier Stoffe durch Diffusion Diffusion (v. lateinisch diffundere ‚ausgießen‘, ‚verstreuen‘, ‚ausbreiten‘) ist ein physikalischer Prozess, der zu einer gleichmäßigen Verteilung von Teilchen und somit …   Deutsch Wikipedia

  • Diffusion (Naturwissenschaft) — Modellhafte Darstellung der Durchmischung zweier Stoffe durch Diffusion Diffusion (v. lat.: diffundere „ausgießen, verstreuen, ausbreiten“) ist ein physikalischer Prozess, der zu einer gleichmäßigen Verteilung von Teilchen und somit zur… …   Deutsch Wikipedia

  • anomale Streuung — anomalioji sklaida statusas T sritis fizika atitikmenys: angl. anomalous scatter vok. anomale Streuung, f rus. аномальное рассеяние, n pranc. diffusion anormale, f …   Fizikos terminų žodynas

  • diffusion anormale — anomalioji sklaida statusas T sritis fizika atitikmenys: angl. anomalous scatter vok. anomale Streuung, f rus. аномальное рассеяние, n pranc. diffusion anormale, f …   Fizikos terminų žodynas

  • Facteur de diffusion atomique — En physique, le facteur de diffusion atomique est une mesure de la puissance de diffusion d une onde par un atome. Il dépend de la nature des interactions entre l onde et l objet diffusant, donc de la radiation incidente : en général, il s… …   Wikipédia en Français

  • Détermination d'une structure cristalline — La détermination d une structure cristalline consiste, de manière générale, à déterminer, pour un cristal de structure inconnue, les paramètres de sa maille conventionnelle, son réseau de Bravais, son groupe d espace et la position des atomes… …   Wikipédia en Français

  • Johannes Martin Bijvoet — (né le 23 janvier 1892 à Amsterdam et mort le 4 mars 1980 à Winterswijk) est un chimiste et cristallographe néerlandais qui travailla au laboratoire van t Hoff de l université d Utrecht. Il est connu pour avoir développé une méthode de… …   Wikipédia en Français

  • Loi de Friedel — La loi de Friedel est une loi utilisée en cristallographie, découverte par le minéralogiste et cristallographe Georges Friedel en 1913[1]. L une des premières étapes de la détermination d une structure cristalline (par diffraction de rayons X, de …   Wikipédia en Français

  • Biologie structurale — Structure 3D de la myoglobine, la première protéine dont la structure a été résolue par cristallographie par John Kendrew en 1958[1]. La biologie structurale est la branche de la biologie qui étudie la structure et l organisation spatiale des… …   Wikipédia en Français

  • Association française de cristallographie — L’Association française de cristallographie (AFC) est une société savante qui rassemble les physiciens, chimistes et biologistes qui utilisent les cristaux et la cristallographie pour leurs recherches ou développent des méthodes en… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”