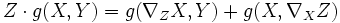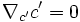Variété pseudo-riemanienne

La géométrie pseudo-riemannienne est une extension de la géométrie riemannienne ; au même titre que, en algèbre bilinéaire, l'étude des formes bilinéaires symétriques généralisent les considérations sur les métriques euclidiennes. Cependant, cette géométrie présente des aspects non intuitifs des plus surprenants.

Définition formelle

Une métrique pseudo-riemannienne sur une variété différentielle M de dimension n est une famille g={g_x} de formes bilinéaires symétriques non dégénérées sur les espaces tangents T_xM de signature constante (p,q). La donnée (M,g) est appelée variété pseudo-riemannienne. La géométrie pseudo-riemannienne est l'étude de ces structures, de leurs particularités et des relations qu'elles entretiennent entre elles.

Les variétés pseudo-riemanniennes représentent une classe importante de variétés différentielles, regroupant en particulier les variétés riemanniennes et les variétés lorentziennes :

• Une variété pseudo-riemannienne est riemannienne lorsque la signature est (n,0) ou (0,n).
  Article détaillé : géométrie riemannienne.
• Une métrique pseudoriemmannienne est dite lorentzienne lorsque la signature est (n-1,1) et (1,n-1).
  Article détaillé : géométrie lorentzienne.

Résultats

Comme en géométrie riemmannienne, il existe une mesure naturelle v sur toute variété pseudo-riemannienne (M,g), localement donnée par l'unique forme volume valant 1 sur toute base pseudo-orthonormée. Si la variété est orientable, la forme volume est globalement définie.

De plus, il existe une unique connexion, appelée connexion de Levi-Cevita, sans torsion, et métrique, au sens où, pour tous champs de vecteurs X, Y et Z, on a :

Les géodésiques sont les courbes c vérifiant :

L'existence d'une connexion de Levi-Cevita implique les conséquences de rigidité suivantes :

• Une isométrie f d'une variété pseudo-riemannienne (M,g), fixant un point m, et telle que df(x) = Id, est l'identité.
• Le groupe d'isométrie d'une variété pseudo-riemannienne de dimension n est un groupe de Lie de dimension finie, au plus n(n + 1) / 2. La classification des variétés pseudo-riemanniennes pour lesquelles l'égalité est vérifiée est connue.

Malheureusement, la norme d'un vecteur n'est pas définie. La particularité de la géométrie riemannienne est qu'elle est à la croisée des géométries pseudo-riemanniennes et des géométries de Finsler. Elle bénéficie donc d'une distance.

En particulier, la notion de complétude d'une variété pseudo-riemannienne se définit sur des propriétés dynamiques.

Une variété pseudo-riemannienne (M,g) est complète lorsque toutes ses géodésiques se définissent sur R ou, de manière équivalente, lorsque le flot géodésique est complet. L'un des miracles de la géométrie riemannienne est que la compacité implique la complétude. La situation est différente en géométrie pseudo-riemannienne : le théorème de Marsden donne des conditions supplémentaires pour obtenir la complétude.

Voir aussi

• Variété riemannienne
• Variété lorentzienne

• Portail de la géométrie