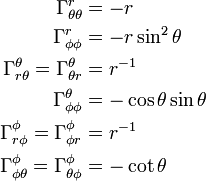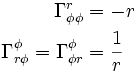- Coefficients de connexion
-
Symboles de Christoffel
En mathématiques et en physique, les symboles de Christoffel, qui tirent leur nom du mathématicien Elwin Bruno Christoffel, sont une expression de la connexion de Levi-Civita dérivée du tenseur métrique. Les symboles de Christoffel sont utilisés dans les calculs pratiques de la géométrie de l'espace : ce sont des outils de calculs concrets, mais en contrepartie leur manipulation est relativement longue, notamment du fait du nombre de termes impliqués.
Ce sont des outils de base utilisés dans le cadre de la Relativité générale pour décrire l'action de la masse et de l'énergie sur la courbure de l'espace-temps.
Au contraire, les notations formelles pour la connexion de Levi-Civita permettent l'expression de résultats théoriques de façon élégante, mais n'ont pas d'application directe pour les calculs pratiques.
Sommaire
Liminaires
Les définitions données ci-dessous sont valides à la fois pour les variétés riemanniennes et les variétés pseudo-riemanniennes, telles que celles utilisées en relativité générale. On utilise de même la notation des indices supérieurs pour les coordonnées contravariantes, et inférieur pour les coordonnées covariantes.
Définition
Dans une variété riemanienne ou pseudo-riemanienne M, il n'existe pas de système de coordonnées qui s'applique à toute la variété. On peut néanmoins définir localement un repère de Lorentz (voir définition d'une variété topologique : on peut trouver en chaque point de M un voisinage ouvert homéomorphe à un ouvert de l'espace
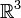 ).
).La dérivée covariante permet d'évaluer l'évolution d'un champ de vecteurs V en prenant en compte non seulement ses modifications intrinsèques, mais aussi celle du système de coordonnées. Ainsi, si on prend un repère en coordonnées polaires, les deux vecteurs er et eθ ne sont pas constants et dépendent du point étudié. La dérivée covariante permet de prendre en compte ces deux facteurs d'évolution.
Les symboles de Christoffel Γkji représentent alors l'évolution des vecteurs de base, à travers leur dérivée covariante :
En utilisant les propriétés de la dérivée covariante, on parvient à l'expression :
Les coordonnées du vecteur
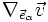 sont notées à l'aide d'un point-virgule, selon la définition :
sont notées à l'aide d'un point-virgule, selon la définition :En remplaçant
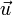 par
par 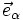 dans la relation ci-dessus, on obtient :
dans la relation ci-dessus, on obtient :On voit donc qu'effectivement l'évolution du vecteur
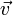 dépend à la fois de son évolution intrinsèque (terme
dépend à la fois de son évolution intrinsèque (terme 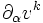 ) et de celle de la base, rattaché au deuxième terme et notamment à Γkjα, symbole de Christoffel.
) et de celle de la base, rattaché au deuxième terme et notamment à Γkjα, symbole de Christoffel.Ce résultat est valable pour un vecteur
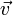 qui est un tenseur d'ordre 1. Pour un tenseur d'ordre n et de rang (l,m), on pourrait obtenir la même chose :
qui est un tenseur d'ordre 1. Pour un tenseur d'ordre n et de rang (l,m), on pourrait obtenir la même chose :Les indices en gras ci-dessous mettent en valeur les contributions des différents composantes de Christoffel. On observe d'ailleurs que les indices contravariants donnent lieu à une contribution positive du coefficient de Christoffel, tandis que les indices covariants à une contribution négative.
Expression par rapport au tenseur métrique
On peut exprimer la valeur des coefficients de Christoffel par rapport au tenseur gik, en prenant en compte le fait que
car la métrique est conservée localement : on a localement un repère de Lorentz en chaque point de l'espace.
En appliquant à g, tenseur d'ordre 2 et de rang (0,2), l'équation des coefficients de Christoffel donnée ci-dessus (2 coordonnées covariantes donnent 2 contributions « négatives ») :
On trouve alors, en permutant les indices et en exprimant plusieurs valeurs des coefficients :
où gij est l'inverse de gij, défini en utilisant le symbole de Kronecker par gkigil = δkl.
Remarque : bien que les symboles de Christoffel soient écrits dans la même notation que les tenseurs, ce ne sont pas des tenseurs. En effet, ils ne se transforment pas comme les tenseurs lors d'un changement de coordonnées.
La plupart des auteurs choisissent des définir les symboles de Christoffel dans une base de coordonnées holonomiques, qui est la convention suivie ici. Dans des coordonnées non holonomiques, les symboles de Christoffel s'expriment dans une formulation plus complexe :
où les
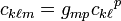 sont les coefficients de commutation de la base, c'est-à-dire
sont les coefficients de commutation de la base, c'est-à-direoù ek sont les vecteurs de base et [.,.] correspond au crochet de Lie. Deux exemples de base non holonomiques sont par exemple celles associées aux coordonnées sphériques ou cylindriques.
Par exemple, les seuls termes non constants du tenseur métrique en coordonnées sphériques sont gθθ = r2, gφφ = r2sin2θ, et l'on a gθθ,r = 2r, gφφ,r = 2rsin2, gφφ,θ = 2r2cosθsinθ. Les éléments non nuls du symbole de Christoffel en fonction du tenseur métrique sont donc peu nombreux :
De même, le seul terme non constant du tenseur métrique en coordonnées cylindriques est gφφ = r2, et l'on a gφφ,r = 2r. Les éléments non nuls du symbole de Christoffel en fonction du tenseur métrique sont donc peu nombreux :
Contraction
Article détaillé : Contraction du symbole de Christoffel.Voir aussi
Bibliographie
- Claude Semay, Bernard Silvestre-Brac, Introduction au calcul tensoriel, Applications à la physique, Dunod, 2007 (ISBN 978-2-10-050552-4)
- Portail de la physique
Catégories : Géométrie riemannienne | Relativité générale
Wikimedia Foundation. 2010.

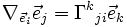
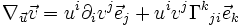
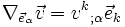
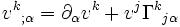
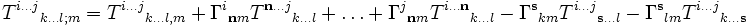
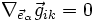
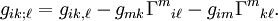
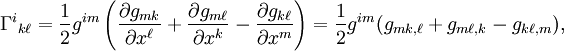
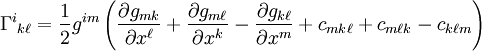
![[e_k,e_\ell] = c_{k\ell}{}^m e_m\,\](/pictures/frwiki/53/578eecd87223ce50c17c9cec073f2dfa.png)