Connexion de Levi-Cevita

Connexion de Levi-Cevita

Connexion de Levi-Civita

En géométrie riemannienne, la connexion de Levi-Civita est une connexion de Koszul naturellement définie sur toute variété riemannienne ou par extension sur toute variété pseudo-riemannienne. Ses propriétés caractérisent la variété riemannienne. Notamment, les géodésiques, courbes minimisant localement la distance riemannienne, sont exactement les courbes pour lesquelles le vecteur vitesse est parallèle. De plus, la courbure de la variété se définit à partir de cette connexion ; des conditions sur la courbure imposent des contraintes topologiques sur la variété.

La connexion de Levi-Civita est appelée en référence au mathématicien italien Tullio Levi-Civita (1873 - 1941) qui a introduit les concepts de transport parallèle pour les besoins de la relativité générale.

Sommaire

Définition

Une métrique pseudo-riemannienne g de classe Ck sur une variété différentielle M est la donnée d'une famille gx de formes bilinéaires symétriques non dégénérées sur les espaces tangents TxM, de sorte que pour tous champs de vecteurs X et Y de clase Ck, la fonction g(X,Y) soit de classe Ck. La signature de g est localement constante sur U. La métrique g est dite riemannienne si en tout point x la forme gx est (définie) positive.

Il existe une unique connexion de Koszul \nabla sur TxM, appelée connexion de Levi-Civita vérifiant les conditions :

  1. \nabla est sans torsion : pour tous champs de vecteurs X et Y, \nabla_XY-\nabla_YX=[X,Y] ;
  2. et g est parallèle : pour tous champs de vecteurs X, Y et Z, on a :
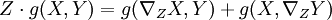Z\cdot g(X,Y)=g(\nabla_ZX,Y)+g(X,\nabla_ZY).


Existence et unicité
Unicité : On commence par établir l'unicité de la connexion de Levi-Civita en supposant que cette dernière existe. La stratégie est la suivante : on cherche une identité définissant implicitement \nabla. A posteriori, cette identité sera utilisée pour définir la connexion recherchée. Comme g est parallèle pour la connexion de Levi-Civita, pour tous champs de vecteurs X, Y et Z, on a :
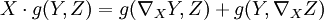X\cdot g(Y,Z)=g(\nabla_XY,Z)+g(Y,\nabla_XZ),
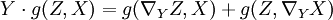Y\cdot g(Z,X)=g(\nabla_YZ,X)+g(Z,\nabla_YX),
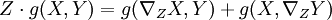Z\cdot g(X,Y)=g(\nabla_ZX,Y)+g(X,\nabla_ZY).
La somme des deux premières identités moins la troisième donne :
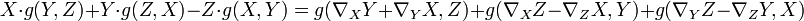
X\cdot g(Y,Z)+Y\cdot g(Z,X)-Z\cdot g(X,Y)=g(\nabla_XY+\nabla_YX,Z) +g(\nabla_XZ-\nabla_ZX,Y)+g(\nabla_YZ-\nabla_ZY,X)
Parce que la torsion est nulle, l'expression précédente se simplifie :
2g(\nabla_XY,Z)=X\cdot g(Y,Z)+Y\cdot g(Z,X)-Z\cdot g(X,Y)+g([X,Y],Z)+g([Z,X],Y)-g([Y,Z],X).
Par non dégénérescence de g, la connexion \nabla est uniquement déterminée par l'égalité ci-dessus.
Existence : Si X et Y sont deux champs de vecteurs sur M, on définit le champ 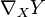\nabla_XY comme l'unique champ de vecteurs sur M vérifiant l'identité précédemment obtenue :
2g(\nabla_XY,Z)=X\cdot g(Y,Z)+Y\cdot g(Z,X)-Z\cdot g(X,Y)+g([X,Y],Z)+g([Z,X],Y)-g([Y,Z],X).
\nabla est bien une connexion de Koszul. En effet, pour toutes fonctions f, on a :
2g(\nabla_X(fY),Z)=X\cdot g(fY,Z)+(fY)\cdot g(Z,X)-Z\cdot g(X,fY)+g([X,fY],Z)+g([Z,X],fY)-g([fY,Z],X)
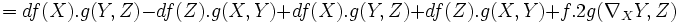
=df(X).g(Y,Z)-df(Z).g(X,Y)+df(X).g(Y,Z)+df(Z).g(X,Y)+f.2g(\nabla_XY,Z)
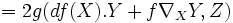=2g(df(X).Y+f\nabla_XY,Z) ;
2g(\nabla_{fX}Y,Z)=(fX)\cdot g(Y,Z)+Y\cdot g(Z,fX)-Z\cdot g(fX,Y)+g([fX,Y],Z)+g([Z,fX],Y)-g([Y,Z],fX)
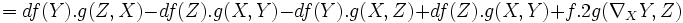
=df(Y).g(Z,X)-df(Z).g(X,Y)-df(Y).g(X,Z)+df(Z).g(X,Y)+f.2g(\nabla_XY,Z)
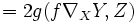=2g(f\nabla_XY,Z).
\nabla est bien sans torsion :
2g(\nabla_XY-\nabla_YX,Z)=X\cdot g(Y,Z)+Y\cdot g(Z,X)-Z\cdot g(X,Y)+g([X,Y],Z)+g([Z,X],Y)-g([Y,Z],X)
-Y\cdot g(X,Z)-X\cdot g(Z,Y)+Z\cdot g(Y,X)-g([Y,X],Z)-g([Z,Y],X)+g([X,Z],Y)
= 2g([X,Y],Z).
Enfin, g est bien parallèle pour la connexion \nabla :
2g(\nabla_XY,Z)+2g(Y,\nabla_XZ)=X\cdot g(Y,Z)+Y\cdot g(Z,X)-Z\cdot g(X,Y)+g([X,Y],Z)+g([Z,X],Y)-g([Y,Z],X)
+X\cdot g(Z,Y)+Z\cdot g(Y,X)-Y\cdot g(X,Z)+g([X,Z],Y)+g([Y,X],Z)-g([Z,Y],X)
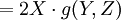=2X\cdot g(Y,Z).
Ainsi, la connexion de Koszul \nabla vérifie toutes les conditions requises.

La démonstration donnée dans la boite déroulante donne une expression implicite de la connexion de Levi-Civita. Toutefois, cette expression est souvent peu utile. Seules les propriétés énoncées dans sa définition suffisent.

Coordonnées locales

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Courbure

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Exemples

Métriques induites

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Métriques conformes

La connexion de Levi-Civita de e2f.g est donnée par :

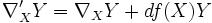
\nabla'_XY=\nabla_XY+df(X)Y
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Connexion de Levi-Civita ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Connexion de Levi-Cevita de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Connection de Levi-Cevita — Connexion de Levi Civita En géométrie riemannienne, la connexion de Levi Civita est une connexion de Koszul naturellement définie sur toute variété riemannienne ou par extension sur toute variété pseudo riemannienne. Ses propriétés caractérisent… …   Wikipédia en Français

  • Tullio Levi-Cevita — Tullio Levi Civita Tullio Levi Civita (29 mars 1873 à Padoue, Italie 29 décembre 1941 à Rome) est un mathématicien italien. Il est connu principalement pour son travail sur le calcul tensoriel et ses applications en théorie de la relativité. Il… …   Wikipédia en Français

  • Variete pseudo-riemannienne — Variété pseudo riemannienne La géométrie pseudo riemannienne est une extension de la géométrie riemannienne ; au même titre que, en algèbre bilinéaire, l étude des formes bilinéaires symétriques généralisent les considérations sur les… …   Wikipédia en Français

  • Variété pseudo-riemanienne — Variété pseudo riemannienne La géométrie pseudo riemannienne est une extension de la géométrie riemannienne ; au même titre que, en algèbre bilinéaire, l étude des formes bilinéaires symétriques généralisent les considérations sur les… …   Wikipédia en Français

  • Geodesique — Géodésique En géométrie, une géodésique désigne le chemin le plus court, ou l un des plus courts chemins s il en existe plusieurs, entre deux points d un espace pourvu d une métrique (un moyen de mesurer les distances). Lorsque l on change cette… …   Wikipédia en Français

  • Géodesiques — Géodésique En géométrie, une géodésique désigne le chemin le plus court, ou l un des plus courts chemins s il en existe plusieurs, entre deux points d un espace pourvu d une métrique (un moyen de mesurer les distances). Lorsque l on change cette… …   Wikipédia en Français

  • Géodésique — En géométrie, une géodésique désigne le chemin le plus court, ou l un des plus courts chemins s il en existe plusieurs, entre deux points d un espace pourvu d une métrique (un moyen de mesurer les distances). Lorsque l on change cette notion de… …   Wikipédia en Français

  • Variete cotangente — Variété cotangente En topologie différentielle, une variété cotangente est l espace total du fibré cotangent d une variété différentielle M. Rappelons que le fibré cotangent est le fibré dual du fibré tangent de M. Ses sections sont les 1 formes… …   Wikipédia en Français

  • Variété cotangente — En topologie différentielle, une variété cotangente est l espace total du fibré cotangent d une variété différentielle M. Rappelons que le fibré cotangent est le fibré dual du fibré tangent de M. Ses sections sont les 1 formes différentielles de… …   Wikipédia en Français

  • Espace De Sobolev — Les espaces de Sobolev sont des espaces fonctionnels. Plus précisément, un espace de Sobolev est un espace vectoriel de fonctions muni de la norme obtenue par la combinaison de la norme norme Lp de la fonction elle même ainsi que de ses dérivées… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”