- Transformée inverse
-
Méthode de la transformée inverse
La méthode de la transformée inverse est une méthode informatique pour produire une suite de nombres aléatoires de distribution donnée, à partir de l'expression de sa fonction de répartition.
Le problème auquel s'adresse cette méthode est le suivant :
- Soit X une variable aléatoire dont la distribution est décrite par la fonction de répartition F(x) ;
- On désire obtenir une suite de réalisations de X.
Cette méthode est fondée sur la propriété qu'a la variable aléatoire U = FX(X) d'être distribuée uniformément sur [0;1] dès que la fonction de répartition FX(x) est continue et strictement croissante sur
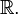La distribution recherchée s'obtient donc comme l'ensemble des antécédents x des tirages u selon une distribution uniforme pour la fonction de répartition FX(x). Autrement dit, la variable aléatoire 
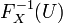a pour loi FX(x), où U est une loi uniforme sur [0;1]. Pour une formulation plus précise, voir le Théorème de la réciproque dans l'article Fonction de répartition.La plupart des langages de programmation permettant de produire des nombres pseudo-aléatoires de distribution uniforme, il suffit de calculer l'antécédent des nombres tirés selon la fonction de distribution FX(x).
Pour certaines lois, on sait inverser FX(x):
- la Loi exponentielle de paramètre λ se tire comme − log(U) / λ;
- la Loi de Cauchy standard se simule comme tan(πU);
- la Loi logistique standard se simule comme log[U / (1 − U)];
- la Loi de Laplace se simule comme − sgn(U)log(1 − 2 | U | ).
Mais la plupart du temps, le calcul de l'antécédent est problématique: on ne sait pas obtenir x vérifiant FX(x) = u, car on ne sait pas inverser la fonction FX. Il faut alors procéder numériquement, pour résoudre en x l'équation FX(x) − u = 0, en utilisant au choix la Méthode de dichotomie, la Méthode de la fausse position, la Méthode de la sécante ou encore la Méthode de Newton.
Voir aussi
- Méthode de rejet
- Cette méthode est aussi importante sur le plan théorique. Voir en particulier le Théorème de la réciproque dans l'article Fonction de répartition.
Références
- Luc Devroye. Non-Uniform Random Variate Generation. New York: Springer-Verlag, 1986. (site) Voir le chapitre 2, section 2, p. 28
Portail de l’informatique
Portail des probabilités et des statistiques
Catégorie : Probabilités
Wikimedia Foundation. 2010.
