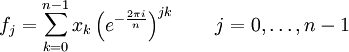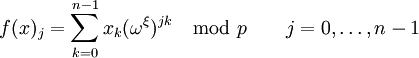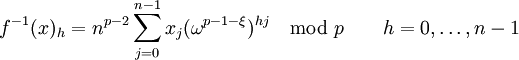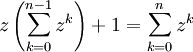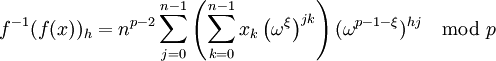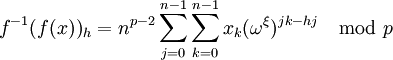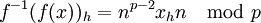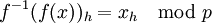Transformee de Walsh

Transformee de Walsh

Transformée de Walsh

En mathématiques, et plus précisément en analyse harmonique la transformée de Walsh est l'analogue de la Transformée de Fourier discrète.

Elle opère sur un corps fini de l'arithmétique modulaire à la place des nombres complexes.

Elle est utilisée en théorie de l'information à la fois pour les codes linéaires et la cryptographie.

Sommaire

Définition

Soit G un groupe abélien fini d'ordre g et d'exposant une puissance nième d'un nombre premier p, Fpn le corps fini de cardinal p n, χ un caractère à valeur dans Fpn et f une fonction de G dans Fpn.

  • La transformée de Walsh est une fonction, souvent noté 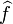\widehat f de l'ensemble des caractères de G dans le corps Fpn définie par :
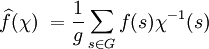
\widehat f (\chi) \ = \frac 1g \sum_{s \in G} f(s)\chi^{-1}(s)

Analyse harmonique sur un groupe abélien fini

Article détaillé : Analyse harmonique sur un groupe abélien fini.

Le contexte est identique à celui de l'analyse harmonique classique d'un groupe abélien fini. La forme bilinéaire associée à l'algèbre du groupe est alors la suivante :

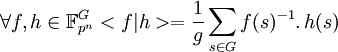
\forall f,h \in \mathbb F_{p^n}^G <f|h>=\frac 1g \sum_{s \in G} f(s)^{-1}.\,h(s) \;

L'ensemble des résultats de la théorie de l'analyse harmonique s'applique, on dispose ainsi de l'égalité de Parseval, du théorème de Plancherel, d'un produit de convolution, de la dualité de Pontryagin ou encore de la formule sommatoire de Poisson.

Cas d'un espace vectoriel fini

Article détaillé : Analyse harmonique sur un espace vectoriel fini.

Il existe un cas particulier, celui ou le groupe G est le groupe additif d'un espace vectoriel fini. Un cas particulier est celui ou G est un corps.

La transformation discrète de Fourier est donnée par

f_j=\sum_{k=0}^{n-1}x_k\left(e^{-\frac{2\pi i}{n}}\right)^{jk}\quad\quad j=0,\dots,n-1

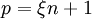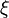La transformation théorique de nombre opère sur une suite de n nombres, modulo un nombre premier p de la forme p = \xi n + 1\,, où \xi\, peut être tout nombre entier positif.

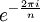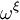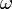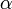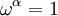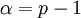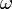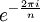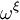Le nombre e^{-\frac{2\pi i}{n}}\, est remplacé par un nombre \omega^{\xi}\, où \omega\, est une « racine primitive » de p, un nombre où le plus petit nombre entier positif \alpha\, où \omega^{\alpha} = 1\, est \alpha = p - 1\,. Il devrait y avoir une quantité d'\omega\, qui collent à cette condition. Les deux nombres e^{-\frac{2\pi i}{n}}\, et \omega^{\xi}\, élevé à la puissance n sont égaux à 1 (mod p), toutes les puissances inférieures différentes de 1.

La transformation théorique de nombre est donnée par

f(x)_j=\sum_{k=0}^{n-1}x_k(\omega^\xi)^{jk}\mod p\quad\quad j=0,\dots,n-1

Contexte

La transformation théorique de nombre inverse est donnée par

f^{-1}(x)_h=n^{p-2}\sum_{j=0}^{n-1}x_j(\omega^{p-1-\xi})^{hj}\mod p\quad\quad h=0,\dots,n-1
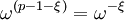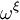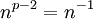\omega^{(p-1-\xi)} = \omega^{-\xi}\,, l'inverse de \omega^{\xi}\,, et n^{p-2} = n^{-1}\,, l'inverse de n. (mod p)

L'inverse est vrai, car 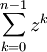\sum_{k=0}^{n-1}z^k est n pour z=1 et 0 pour tous les autres z où 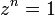z^n = 1\,. Une démonstration de ceci (devrait marcher pour toute algèbre de division) est

z\left(\sum_{k=0}^{n-1}z^k\right)+1=\sum_{k=0}^nz^k
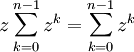z\sum_{k=0}^{n-1}z^k=\sum_{k=0}^{n-1}z^k (soustrayant z^n = 1\,)
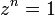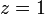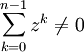z=1\, si \sum_{k=0}^{n-1}z^k\ne 0 (divisant les deux cotés)

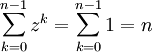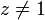Si z=1 alors nous pouvions voir de manière triviale que \sum_{k=0}^{n-1}z^k=\sum_{k=0}^{n-1}1=n. Si z \ne 1\, alors le coté droit doit être faux pour éviter une contradiction.

Nous pouvons maintenant compléter la démonstration. Nous prenons la transformation inverse de la transformation.

f^{-1}(f(x))_h=n^{p-2}\sum_{j=0}^{n-1}\left(\sum_{k=0}^{n-1}x_k\left(\omega^\xi\right)^{jk}\right)(\omega^{p-1-\xi})^{hj}\mod p
f^{-1}(f(x))_h=n^{p-2}\sum_{j=0}^{n-1}\sum_{k=0}^{n-1}x_k(\omega^\xi)^{jk-hj}\mod p
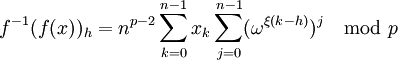
f^{-1}(f(x))_h=n^{p-2}\sum_{k=0}^{n-1}x_k\sum_{j=0}^{n-1}(\omega^{\xi(k-h)})^j\mod p
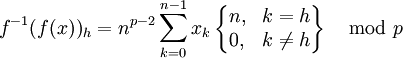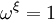f^{-1}(f(x))_h=n^{p-2}\sum_{k=0}^{n-1}x_k\left\{\begin{matrix}n,&k=h\\0,&k\ne h\end{matrix}\right\}\mod p (puisque \omega^{\xi} = 1\,)
f^{-1}(f(x))_h=n^{p-2}x_hn\mod p
f^{-1}(f(x))_h=x_h\mod p

Voir aussi

Lien externe

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Transform%C3%A9e de Walsh ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Transformee de Walsh de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Transformée de walsh — En mathématiques, et plus précisément en analyse harmonique la transformée de Walsh est l analogue de la Transformée de Fourier discrète. Elle opère sur un corps fini de l arithmétique modulaire à la place des nombres complexes. Elle est utilisée …   Wikipédia en Français

  • Transformée de Walsh — En mathématiques, et plus précisément en analyse harmonique la transformée de Walsh est l analogue de la Transformée de Fourier discrète. Elle opère sur un corps fini de l arithmétique modulaire à la place des nombres complexes. Elle est utilisée …   Wikipédia en Français

  • Transformee de Hadamard — Transformée de Hadamard La transformée d´Hadamard (aussi connue sous le nom de « transformée de Walsh Hadamard ») est un exemple d une classe généralisée d une transformée de Fourier. Elle est nommée d après le mathématicien français… …   Wikipédia en Français

  • Transformée de hadamard — La transformée d´Hadamard (aussi connue sous le nom de « transformée de Walsh Hadamard ») est un exemple d une classe généralisée d une transformée de Fourier. Elle est nommée d après le mathématicien français Jacques Hadamard et… …   Wikipédia en Français

  • Transformée de Hadamard — La transformée d´Hadamard (aussi connue sous le nom de « transformée de Walsh Hadamard ») est un exemple d une classe généralisée d une transformée de Fourier. Elle est nommée d après le mathématicien français Jacques Hadamard et… …   Wikipédia en Français

  • Transformée — En mathématiques, une transformée consiste à associer une fonction à une autre fonction. Liste des transformées Transformée de Fourier Transformée de Fourier discrète Transformée de Fourier rapide Transformée de Fourier locale Transformée de… …   Wikipédia en Français

  • Walsh — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sommaire 1 Patronyme 2 Personnage fictif 3 …   Wikipédia en Français

  • Transformation de Hadamard-Walsh — Transformée de Hadamard La transformée d´Hadamard (aussi connue sous le nom de « transformée de Walsh Hadamard ») est un exemple d une classe généralisée d une transformée de Fourier. Elle est nommée d après le mathématicien français… …   Wikipédia en Français

  • Fonction De Walsh — 1 2 3 4 5 6 7 8 Table des huit premières fonctions orthogonales d une base orthogonale Les fonctions de Walsh sont un ensemble de fonctions qui forment une base orthogonale sur l intervalle [0;1] pour les fonctions qui respectent la condition… …   Wikipédia en Français

  • Fonction de walsh — 1 2 3 4 5 6 7 8 Table des huit premières fonctions orthogonales d une base orthogonale Les fonctions de Walsh sont un ensemble de fonctions qui forment une base orthogonale sur l intervalle [0;1] pour les fonctions qui respectent la condition… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”