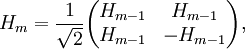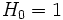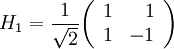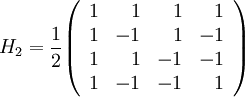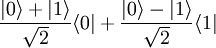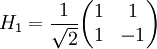Transformee de Hadamard

Transformee de Hadamard

Transformée de Hadamard

La transformée d´Hadamard (aussi connue sous le nom de « transformée de Walsh-Hadamard ») est un exemple d'une classe généralisée d'une transformée de Fourier. Elle est nommée d'après le mathématicien français Jacques Hadamard et effectue une opération linéaire et involutive avec une matrice orthogonale et symétrique sur 2m nombres réels (ou complexes, bien que les matrices utilisées possèdent des coefficients réels). Ces matrices sont des matrices de Hadamard.

La transformée de Hadamard peut être vue comme étant issue d'une transformée de Fourier discrète et s'avère être en fait l'équivalent d'une transformée de Fourier discrète multidimensionnelle d'une taille de 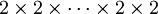2\times2\times\cdots\times2\times2. Elle décompose un vecteur arbitraire en entrée en une superposition de fonctions de Walsh.

Définition formelle

La transformée de Hadamard Hm utilise une matrice 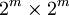2^m \times 2^m (une matrice de Hadamard) multipliée par un facteur de normalisation, et transforme 2m nombres réels xn en 2m nombres réels Xk. La transformée peut être définie de deux manières : récursivement ou en utilisant une représentation binaire des indices n et k.

Récursivement, on définit une première transformation 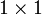1\times1 via une matrice H0 qui est la matrice identité avec un seul élément (1). On définit ensuite Hm pour m > 0 grâce à la relation suivante :

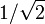H_m = \frac{1}{\sqrt2} \begin{pmatrix} H_{m-1} & H_{m-1} \\ H_{m-1} & -H_{m-1} \end{pmatrix},

où 1/\sqrt2 est un facteur de normalisation qui est parfois omis. Ainsi, à l'exception de la normalisation, les coefficients de la matrice sont égaux à 1 ou -1.

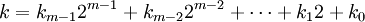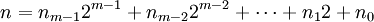De manière équivalente, on peut définir l'élément (k,n) d'une matrice de Hadamard grâce à k=k_{m-1} 2^{m-1} + k_{m-2} 2^{m-2} + \cdots + k_1 2 + k_0 etn=n_{m-1} 2^{m-1} + n_{m-2} 2^{m-2} + \cdots + n_1 2 + n_0, où kj etnj sont le bit j (0 ou 1) de respectivement n et k. Dans ce cas, on obtient

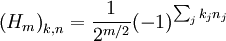\left( H_m \right)_{k,n} = \frac{1}{2^{m/2}} (-1)^{\sum_j k_j n_j}.

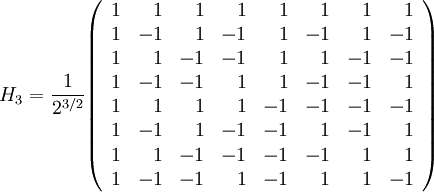
Il s'agit d'une transformée de Fourier discrète 2\times2\times\cdots\times2\times2 normalisée de manière à être unitaire, si l'on considère les entrées et les sorties comme des tableaux multidimensionnels indexés par nj et kj.

Quelques matrices de Hadamard :

~H_0 = 1
H_1 = \frac{1}{\sqrt2} \begin{pmatrix}\begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array}\end{pmatrix}
H_2 = \frac{1}{2} \begin{pmatrix}\begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1\end{array}\end{pmatrix}
H_3 = \frac{1}{2^{3/2}} \begin{pmatrix}\begin{array}{rrrrrrrr} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 & 1 & -1 & -1 & 1 \\ 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1\\ 1 & -1 & 1 & -1 & -1 & 1 & -1 & 1 \\ 1 & 1 & -1 & -1 & -1 & -1 & 1 & 1 \\ 1 & -1 & -1 & 1 & -1 & 1 & 1 & -1 \end{array}\end{pmatrix}

Les lignes d'une matrice de Hadamard forment des fonctions de Walsh.

Applications

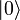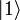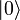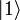Dans le traitement de l'informatique quantique, la transformation de Hadamard, plus souvent appelée « porte de Hadamard » dans ce contexte, est une rotation d'un qubit. Elle permet de transformer les états |0 \rangle et |1 \rangle du qubit en deux états superposés avec un poids égal : |0 \rangle et |1 \rangle . En général, les phases sont choisies de telle manière que :

\frac{|0\rangle+|1\rangle}{\sqrt{2}}\langle0|+\frac{|0\rangle-|1\rangle}{\sqrt{2}}\langle1|

dans la notation de Dirac. Cela correspond à la matrice de transformation :

H_1=\frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}

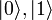dans la base |0 \rangle , |1 \rangle .

Un grand nombre d'algorithmes quantiques utilisent la transformation de Hadamard comme première étape, puisque elle transforme n qubits initialisés avec |0› en une superposition de tous les 2n états orthogonaux exprimés dans la base 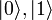|0 \rangle , |1 \rangle avec une pondération égale.

À titre d'exemple, l'algorithme de Shor fait appel à une telle transformation.

Autres applications

La transformation est utilisée en cryptographie, on parle alors de pseudo-transformation de Hadamard. Elle est aussi utilisée pour générer des nombres aléatoires à partir d'une distribution gaussienne. On l'utilise aussi dans la compression de données comme dans l'algorithme H.264 et pour des opérations de traitement du signal.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Transform%C3%A9e de Hadamard ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Transformee de Hadamard de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Transformée de hadamard — La transformée d´Hadamard (aussi connue sous le nom de « transformée de Walsh Hadamard ») est un exemple d une classe généralisée d une transformée de Fourier. Elle est nommée d après le mathématicien français Jacques Hadamard et… …   Wikipédia en Français

  • Transformée de Hadamard — La transformée d´Hadamard (aussi connue sous le nom de « transformée de Walsh Hadamard ») est un exemple d une classe généralisée d une transformée de Fourier. Elle est nommée d après le mathématicien français Jacques Hadamard et… …   Wikipédia en Français

  • Hadamard — Jacques Hadamard Jacques Hadamard Jacques Salomon Hadamard Naissance 8 décembre 1865 Versailles (France) Décès 17& …   Wikipédia en Français

  • Transformée — En mathématiques, une transformée consiste à associer une fonction à une autre fonction. Liste des transformées Transformée de Fourier Transformée de Fourier discrète Transformée de Fourier rapide Transformée de Fourier locale Transformée de… …   Wikipédia en Français

  • Transformation de Hadamard-Walsh — Transformée de Hadamard La transformée d´Hadamard (aussi connue sous le nom de « transformée de Walsh Hadamard ») est un exemple d une classe généralisée d une transformée de Fourier. Elle est nommée d après le mathématicien français… …   Wikipédia en Français

  • Matrice De Hadamard — Une matrice de Hadamard, du nom du mathématicien français Jacques Hadamard, est une matrice carrée dont les coefficients sont tous 1 ou 1 et dont les lignes sont toutes orthogonales entre elles. Le nom retenu pour ces matrices rend hommage au… …   Wikipédia en Français

  • Matrice de Hadamard — Une matrice de Hadamard est une matrice carrée dont les coefficients sont tous 1 ou 1 et dont les lignes sont toutes orthogonales entre elles. Le nom retenu pour ces matrices rend hommage au mathématicien français Jacques Hadamard, même si les… …   Wikipédia en Français

  • Matrice de hadamard — Une matrice de Hadamard, du nom du mathématicien français Jacques Hadamard, est une matrice carrée dont les coefficients sont tous 1 ou 1 et dont les lignes sont toutes orthogonales entre elles. Le nom retenu pour ces matrices rend hommage au… …   Wikipédia en Français

  • Jacques-Salomon Hadamard — Jacques Hadamard Jacques Hadamard Jacques Salomon Hadamard Naissance 8 décembre 1865 Versailles (France) Décès 17& …   Wikipédia en Français

  • Jacques Hadamard — Jacques Salomon Hadamard Naissance 8 décembre 1865 Versailles (France) Décès 17 octobre 1963 …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”