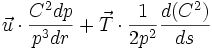- Théorème de siacci
-
Théorème de Siacci
Le théorème de Siacci est un théorème de cinématique qui s'applique aux courbes planes paramétrées par la distance à l'origine et la distance de l'origine à la podaire.
Il peut servir utilement dans le cas de force centrale. Isaac Newton a beaucoup utilisé les formules de Siacci dans ce cas simple.
Sommaire
Énoncé
Les composantes de l'accélération
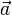 sont selon la direction radiale OM et selon la tangente :
sont selon la direction radiale OM et selon la tangente :où R désigne le rayon de courbure, s désigne l'abscisse curviligne et C = L/m est le moment cinétique par unité de masse, non constant a priori (mais seul C² intervient, comme d'habitude (invariance ré-si de la chimie !).
La première composante s'appelle formule de Newton. Comme dp/dr = r/R , elle se note aussi -1/2.C².d(1/p²)/dr. Alors les Anciens remarquaient que la donnée de la trajectoire en podaire p = f(r) résolvait le problème direct des forces centrales : la trajectoire (T) donne la force centrale.
Exemple : champ central newtonien
- Dans le cas d'un champ central, le théorème de Siacci donne la composante centrale et C = cste. On pose souvent W= C/p.
Alors dans le cas elliptique, avec pour centre de force le foyer, il vient W²/2 = 1/r -1/2a (formule évidente si l'on pense A CONTRARIO au théorème de l'énergie cinétique de Leibniz). Alors cette formule rendit célèbre Newton, puisqu'elle lui donna, dans le de Motu de 1684, la première démonstration du problème direct des lois de Kepler : la force est en -1/r², par application directe du théorème de Siacci.
- Dans le cas de Hooke, a²b².W² = a² + b² -r² , Newton obtint la force
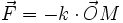
- dans le cas du cercle, avec le centre de force sur le cercle : F = -k/r^5 ( car p ~ r²)
- dans le cas de la spirale logarithmique, p = k r , donc F ~ -k/r^3
- dans le cas des courbes
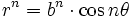 ,
, 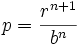 ,
,
alors : F = k/r^(2n+3)
soit n=-2 (hyperbole : Hooke en Symétrie de Corinne) : F = +k r
n=-1 : ligne et force nulle
n= -1/2 : parabole et foyer : F = 1/r² (cas d'énergie nulle)
n= 1/2 : c'est l'inverse de la parabole, donc c'est la cardioïde : F = k/r^4
n= 1 , déjà vu, c'est le cercle.
n= 2 c'est la lemniscate : F= k/r^7
Quasiment tous ces cas sont traités dans les Principia ! Il est clair que Newton, sans le dire explicitement, avait parfaitement compris ce théorème sur les podaires.
Démonstration
Soit (T) la trajectoire de point courant P , de point voisin Q, ANTÉRIEUR de dt (toute l'astuce est là !), de centre de courbure C, et OH la parallèle à CP qui coupe la "tangente" PQ en H ; alors CP : = R , rayon de courbure; et OH := p , H décrivant la podaire de (T) prise par rapport à l'origine O . Et QR la parallèle à CP qui coupe OP en O'. La non-constante des aires est C = p.v. Le triangle infinitésimal PQO' est semblable à PHO :
donc dp/r = dr/R !
- Lemme : Rappel de cinématique de Frenet :
si
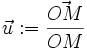 , alors
, alors 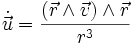 . fin de lemme.
. fin de lemme.L'accélération selon Frenet est sur la tangente dv/dt = 1/2 . d(v²)/ds ; sur la normale v²/R .
Décomposer le vecteur normal selon la radiale et la tangente :
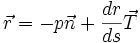
D'où la composante radiale : (v²/R) .(r/p) = C².r / (p³.R) (formule de Newton)
Et la composante tangentielle :
1/2.d(v²)/ds + (v²/R) (r/p)(dr/ds) = (1/2p²). [p²d(v²) + v².2p.dp] /ds = 1/2 . d(C²)/p²ds .
CQFD
- La formule précédente de Frenet (qui a été utilisée) est souvent utilisée aussi pour démontrer l'existence du vecteur de Runge-Lenz : en effet , elle donne immédiatement l'hodographe circulaire du mouvement keplerien par intégration, r/\v = Lo/m étant constant.
Rappel : pour tout mouvement sur une conique de paramètre Po, |a/\v|.Po = C³/r^3 ( cf Théorème de Newton-Hamilton ). Cela donne la démonstration suivante : comme |a/\v|= aC/r si l'accélération est centrale , alors a ~ 1/r².
Newton et les podaires
Le mouvement keplerien est démontré par Newton en 1684 dans le deMotu. Puis dans le corollaire 1 des Propositions 11-13 de la section III du livre 1. Le 11 octobre 1709, Newton écrit à Roger Cotes, en vue de la réédition (1713) des Principia, quelques précisions : Soit S le soleil, P la planète, V sa vitesse. Alors il n'existe qu'une conique ayant S comme centre de force centrale en 1/r².
Ceci était nécessaire pour contrer les arguties de Bernouilli, concernant le problème direct et le problème inverse (à l'évidence, le cas de la spirale logarithmique de Newton posait problème !).
Bien sûr, si l'on multiplie l'accélération par la vitesse, on doit retrouver le théorème de Leibniz :
effectivement 2 a.v = -2C²/p^3 .dp/dt + 1/p².dC²/dt = d ( C²/p2)/dt
On comprend pourquoi le couple W := C/p et r marchait bien : il exprimait dans le cas central le théorème de Leibniz, c’est-à-dire la conservation de l'énergie.
Voir aussi
Articles connexes
- Accélération de Siacci
- Binet: les formules de Binet sont en fonction de
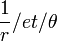
- Force centrale
- Mouvement à force centrale
- Transmutation de la force
- Théorème de Newton-Hamilton
- Temps newtonien
- Mouvement keplerien
- Exégèse des Principia
- Principia et Calculus
Liens et documents externes
- Newton et les podaires, Pourciau in Arch. of Hist. sciences, 1996 (contient 22 références sur ce sujet).
- The sheer joy of celestial mechanics, Grossman, 1996, Éd. Birkhauser, ISBN 3-7643-3832-6, p. 28-30.
- Laplace, mécanique céleste, 1798-1825, ed Bachelier.
- Hérivel, background to Newton's Principia, 1965; ed OUP.
- Cushing, American Journal of physics, 50(1982)617-628.
- Portail de la physique
Catégories : Mécanique du point | Théorème de physique
Wikimedia Foundation. 2010.