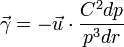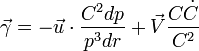- Acceleration de Siacci
-
Accélération de Siacci
En mécanique rationnelle, les composantes de l'accélération dans différents systèmes de coordonnées sont bien connues.
Dans le cas de courbes planes, on utilise souvent les coordonnées polaires (r, θ).
Moins connu, est le système utilisant la définition de la courbe comme antipodaire : Soit O l'origine et P la projection de O sur la tangente en M à la courbe (C) : le point P décrit alors la podaire de O à la courbe (C) : on appelle p la distance OP. Réciproquement la perpendiculaire à la podaire au point P enveloppera la courbe (C) à étudier.
L'exemple classique est : soit un cercle et un point O intérieur ; l'antipodaire est une ellipse de foyer O ,
L'accélération de Siacci exprime l'accélération d'un point en mouvement, M , sur (C) en fonction de sa distance au point O ( on pose OM := r ) et de la distance de O à la podaire ( on pose OP := p).
Cette accélération est très utile dans le cas d'une Force centrale.
Le deuxième paragraphe donne les composantes de cette accélération dans le cas général : moins utile , elle permet néanmoins au néophyte en mécanique de bien comprendre la différence entre projections et composantes, puisque la base utilisée sera non-orthogonale.
Sommaire
Formule de Siacci : cas d'une force centrale
Newton est sans doute un des premiers à avoir graspé cette formule. Ceci dit, la démonstration qu'il en donne est purement géométrique et assez difficile à appréhender.
Ici, est utilisée la formule de Leibniz : dW = F(r).dr = mv.dv , car elle conduit plus simplement au résultat:
Soit C la constante des aires ( = p.v) ; alors :
La formule est alors remarquable, car le temps n'y intervient plus explicitement (il est masqué dans C²) ; si l'on connaît l'expression podaire de la trajectoire r = f(p) ou p = g(r), alors on obtient directement la loi de force F(r)!
Utilisation
- L'exemple classique est celui de Isaac Newton ( nov 1684): pour une ellipse , l'équation podaire vue de son foyer est :a²/p² = 2a/r -1 (cf (note) )
En dérivant cette équation, on obtient -(a²/p³) dp= -(2a/r²) dr. D'où le résultat demandé par Edmund Halley (août 1684): F(r) est en 1/r² !
- Newton (1687) l'utilise maintes fois , cf Exégèse des Principia (spirales logarithmiques , transmutation de la force, ...) .
- Exemple : spirale logarithmique parcourue à vitesse angulaire W constante. Alors l'accélération centrale reste proportionnelle à 1/r³, puisque p = r.sinα= r.k (eadem mutata resurgo, dixit Jacques Bernoulli). C'est la proposition IX.
- Exemple : ellipse de Robert Hooke :l'équation podaire est ab/p² = a²+ b² + r² ; il en résulte que F(r) = -m (C²/a²b²) OM .c'est la proposition X.
- Exemple : O sur le cercle de diamètre "vertical" OA [ A(0,2R) ]. la podaire est immédiate p = r²/2R : d'où F(r) = -m 8C²R²/r⁵ : proposition VII, corollaire I.
- Exemples divers : les courbes r^k = a^k cos kθ ont pour podaires:
p = r^(k+1)/a^k , et donc F(r) = - C² aç(2k) (k+1)/ r^(2k+3) : soit les cas :
- k= 1 , le cercle et F ~ 1/ r^5
- k=2, la lemniscate : F ~ 1/r^7
- k=-2 , l'hyperbole équilatère ( symétrie de Corinne de Hooke) : F ~ +OM.
- k= -1 (n+1)=0 donc pour la ligne , F= 0
- k=1/2 , cardioïde et son origine O : F ~ 1/r^4
- k= -1/2 : la parabole et O au foyer ( cas de Briggs) : F ~ 1/r^2.
- (Note : dans une ellipse il y a deux foyers, avec r+r' = 2a et pp' = a² et p'/r' =p/r).
Démonstration de la formule
- Cas de force centrale :
Alors C = cste. Le travail élémentaire de la Force vaut : F(r).dr = m v.dv, or v² = C²/p² , donc F(r)/m = - C²/p³ . dp/dr
Formule générale de Siacci
Elle décompose l'accélération selon OM et V, ce qui semble assez raisonnable comme choix de base, et pourtant, bien évidemment la base de Frenet est largement plus facile à utiliser!
Remarquer d'abord l'homogénéité, (1/C)dC/dt homogène à l'inverse d'un temps. Remarquer le Choix d'écrire avec C² plutôt qu'avec C , car on ne peut distinguer entre le plan vu de dessus ou vu de dessous. En règle générale, on prend C positif , MAIS ICI , C(t) est variable !De plus le changement t en -t , ne change pas l'accélération.
Remarquable aussi est le fait que le premier terme ( radial) ne change pas entre la formule force centrale et la formule générale. Certes, le deuxième terme contient dC/dt en facteur.
Lemme connu utilisé : ( r dr) = p . R avec R :=rayon de courbure.(cf note)
Démonstration : on va se contenter d'identifier la formule à celle de Frenet.
Le deuxième terme (1/C)dC/dt = (1/v)dv/dt + un terme A = (1/p)dp/dt.
Il reste donc à démontrer que V. A + le terme radial est normal et égal à v²/R N.
Écrire OM = OP + PT = -p N + (r.T) T = -p N +(r.V) V/v².
La projection de Frenet sur N s'écrit : + (C²/rp³) dp/dr .p= v² .dp/(r.dr) =v²/R
La projection de Frenet sur T s'écrit : (v/p)dp/dt - (C²/rp³).(dp/dr).(r.V) / v ;
Or (r.V) = (r dr)/dt , d'où (v/p)dp/dt - (v²/rp) dp/dt.(r dr)/v qui s'annule.
Remarque : dans le deuxième terme on peut faire disparaître le temps : T (1/p²)dC/ds.
- Note : voici une démonstration : p = -r.N donc dp = -dr.N + r.dN = 0+ r.T dα = (r.T)ds / R = r dr/ R . CQFD.
Voir aussi
- Théorème de Siacci
- Accélération
- Cinématique
- Podaire
- Spirale logarithmique
- Transmutation de la force
- Théorème de Newton-Hamilton
- Portail de la physique
Catégorie : Mécanique
Wikimedia Foundation. 2010.