Théorème de la médiane

Le théorème de la médiane, ou théorème d'Apollonius, est une relation entre la longueur d'une médiane d'un triangle et la longueur de ses côtés.

Il existe plusieurs versions de ce théorème dont certaines font appel au produit scalaire.

Enfin, il existe aussi une relation vectorielle liant les vecteurs portés par les côtés et celui porté par la médiane.

Sommaire

1 Théorème de la médiane pour un triangle rectangle
2 Premier théorème de la médiane ou théorème d'Apollonius
- 2.1 Démonstration par le produit scalaire
- 2.2 Démonstration n'utilisant que les théorèmes sur les distances
3 Deuxième théorème de la médiane
4 Troisième théorème de la médiane
5 Forme vectorielle du théorème de la médiane
6 Généralisation du théorème de la médiane à toute cévienne
- 6.1 Démonstration par produit scalaire
7 Voir aussi

Théorème de la médiane pour un triangle rectangle

Il existe un théorème de la médiane relatif au triangle rectangle

Théorème de la médiane - Dans tout triangle rectangle, la longueur de la médiane relative à l'hypoténuse est égale à la moitié de la longueur de l'hypoténuse.

Ce théorème possède une réciproque.

Réciproque du théorème de la médiane - Si dans un triangle, la longueur de la médiane relative à un côté est égale à la moitié de la longueur de ce côté, alors ce triangle est rectangle en le sommet opposé à ce côté.

Premier théorème de la médiane ou théorème d'Apollonius

Théorème d'Apollonius — Soit ABC un triangle quelconque, et AI la médiane issue de A. On a alors la relation suivante :

$AB^2 + AC^2 = 2BI^2 + 2AI^2\,$

Ou encore :

$AB^2 + AC^2 = {1 \over 2} BC^2 + 2AI^2\,$

Démonstration par le produit scalaire

Cette propriété est un cas simple de la réduction de la fonction scalaire de Leibniz : Il suffit de faire intervenir le point I dans chacun des deux carrés :

$AB^2 + AC^2 =(\overrightarrow{AI} + \overrightarrow{IB})^2 + (\overrightarrow{AI} + \overrightarrow{IC})^2$

On développe :

$AB^2+ AC^2 = AI^2 + IB^2 + 2\overrightarrow{AI}.\overrightarrow{IB} + AI^2 + IC^2 + 2\overrightarrow{AI}.\overrightarrow{IC}$

Le point I est milieu de [BC], donc $\overrightarrow{IB}$ et $\overrightarrow{IC}$ sont opposés, ce qui implique que les produits scalaires s'éliminent et $I C 2 = I B 2$ donc

$AB^2+ AC^2 = 2AI^2 + 2IB^2 \,$

Démonstration n'utilisant que les théorèmes sur les distances

Une autre méthode, probablement celle d'Apollonius (comme il ne connaissait pas la fonction scalaire de Leibniz) est la suivante:

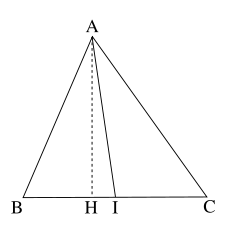
Soit H le pied de la hauteur issue de A. Nous avons BHA et AHC deux triangles rectangles; en y appliquant le théorème de Pythagore, on obtient :

$AB^2 = BH^2 + AH^2 \,$

$AC^2 = AH^2 + HC^2\,$

$AI^2 = IH^2 + AH^2\,$

On obtient donc:

$AB^2 + AC^2 = BH^2 + 2AH^2 + HC^2\,$

On exprime d'une nouvelle manière BH et HC en fonction de BI et IH (en gardant en tête que I est le milieu de BC et donc BI=IC). Notez aussi que dans ce cas en particulier, le pied H de la hauteur issue de A "atterrit" sur le segment [BI], autrement dit entre B et I, mais cela marche pour tous les cas:

$BH = BI - IH \,$

$HC = IC + IH = BI + IH\,$

On remplace maintenant dans l'expression précédente :

$AB^2 + AC^2 = (BI-IH)^2 + 2AH^2 + (BI+IH)^2 \,$

$AB^2 + AC^2 = BI^2 - 2BI.IH+ IH^2 + 2AH^2 + BI^2 + 2BI.IH + IH^2\,$

$AB^2 + AC^2 = 2BI^2 + 2IH^2 + 2AH^2 = 2BI^2 + 2(IH^2 + AH^2) \,$

Or, on sait que, d'après les triangles rectangles du départ:

$IH^2 + AH^2 = AI^2\,$

En remplaçant dans l'égalité précédente, on obtient:

$AB^2 + AC^2 = 2BI^2 + 2AI^2\,$

Deuxième théorème de la médiane

Deuxième théorème de la médiane — Soient (ABC) un triangle et I le milieu du segment [BC]. Alors

$\overrightarrow{AB}\cdot\overrightarrow{AC} = AI^2 - \dfrac 14 BC^2$

La démonstration utilise la relation de Chasles et les identités remarquables. il suffit d'exprimer les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ en fonction de $\overrightarrow{AI}$ et $\overrightarrow{IB}$ .

Troisième théorème de la médiane

Troisième théorème de la médiane — Soient (ABC) un triangle et I le milieu du segment [BC]. On note H le projeté orthogonal de A sur (BC). Alors

$\left|AB^2 - AC^2\right| = 2 BC \times IH$ .

Il suffit d'utiliser le produit scalaire et les identités remarquables :

$AB^2 - AC^2 = ( \overrightarrow{AB} + \overrightarrow{AC})\cdot(\overrightarrow{AB}-\overrightarrow{AC})$

$AB^2 - AC^2 =2 \overrightarrow{AI} \cdot\overrightarrow{CB}$

La projection de $\overrightarrow{AI}$ sur $\overrightarrow{BC}$ est $\overrightarrow{HI}$ d'où

$AB^2 - AC^2 =2 \overrightarrow{HI} \cdot\overrightarrow{CB}$

Ce produit scalaire de deux vecteurs colinéaires est égal à $BC \times IH$ ou son opposé, d'où la valeur absolue.

Forme vectorielle du théorème de la médiane

Soit I le milieu [BC], on a : $\overrightarrow{AB} + \overrightarrow{AC} = 2\overrightarrow{AI}$

Généralisation du théorème de la médiane à toute cévienne

Soit ABC un triangle. Une droite issue de A coupe [BC] en I. Soit $k = \frac {IC}{IB}$ . Alors :

$AI^2=\frac{k AB^2 + AC^2}{1+k} - IB \times IC$

Démonstration par produit scalaire

Il suffit de calculer la combinaison des deux carrés :

$k AB^2 + AC^2 = k(\overrightarrow{AI} + \overrightarrow{IB})^2 + (\overrightarrow{AI} + \overrightarrow{IC})^2$ .

On développe :

$k AB^2+ AC^2 = k(AI^2 + IB^2 + 2\overrightarrow{AI}.\overrightarrow{IB}) + AI^2 + IC^2 + 2\overrightarrow{AI}.\overrightarrow{IC}$

Le point I est le barycentre de (B, k) et (C, 1), donc $k \overrightarrow{IB} + \overrightarrow{IC} = \overrightarrow{0}$ , ce qui élimine les deux produits scalaires.

et IC = k IB donc $k IB^2 + IC^2 = k IB^2 + k^2 IB^2 = k(1+k) IB^2 = (1+k) IB \times IC$ ,

d'où

$k AB^2+ AC^2 = (1+k) (AI^2 + IB \times IC)$ .

Et le résultat en divisant par 1 + k.

Voir aussi

Théorème de projection sur un convexe fermé, dont le présent théorème est un argument clé
Théorème de Stewart

Portail de la géométrie

Catégories :

Théorème de géométrie
Géométrie du triangle

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de la médiane de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Theoreme de la mediane — Théorème de la médiane Le théorème de la médiane, ou théorème d Apollonius, est une relation entre la longueur d une médiane d un triangle et la longueur de ses côtés. Il existe plusieurs versions de ce théorème dont certaines font appel au… … Wikipédia en Français
Théorème d'Apollonius — Théorème de la médiane Le théorème de la médiane, ou théorème d Apollonius, est une relation entre la longueur d une médiane d un triangle et la longueur de ses côtés. Il existe plusieurs versions de ce théorème dont certaines font appel au… … Wikipédia en Français
Theoreme de Stewart — Théorème de Stewart Théorème de Stewart En géométrie euclidienne, le théorème de Stewart est une généralisation du théorème de la médiane due au mathématicien Matthew Stewart dans les années 1746. Enoncé Théorème … Wikipédia en Français
Théorème de stewart — En géométrie euclidienne, le théorème de Stewart est une généralisation du théorème de la médiane due au mathématicien Matthew Stewart dans les années 1746. Enoncé Théorème … Wikipédia en Français
Théorème de Stewart — En géométrie euclidienne, le théorème de Stewart est une généralisation du théorème de la médiane due au mathématicien Matthew Stewart dans les années 1746. Enoncé Théorème Soit … Wikipédia en Français
Médiane (géométrie) — Pour les articles homonymes, voir Médiane. Dans son sens le plus courant, une médiane désigne, dans un triangle, une droite joignant un des sommets du triangle au milieu du côté opposé. Par extension, en géométrie plane, les médianes d un… … Wikipédia en Français
Théorème de Pythagore — Relation entre les longueurs des cô … Wikipédia en Français
Médiane (statistiques) — Pour les articles homonymes, voir Médiane. En théorie des probabilités et en statistiques, la médiane d un ensemble de valeurs (échantillon, population, distribution de probabilités) est la valeur m telle que le nombre de valeurs de l ensemble… … Wikipédia en Français
Théorème central limite — Pour les articles homonymes, voir TCL. La loi normale, souvent appelée la « courbe en cloche » Le théorème central li … Wikipédia en Français
Théorème de Dini — Théorèmes de Dini En topologie, les théorèmes de Dini énoncent des conditions sous lesquelles la convergence simple implique la convergence uniforme. Ce théorème porte le nom du mathématicien italien Ulisse Dini (14 novembre 1845 28 octobre 1918) … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de la médiane

Sommaire

Théorème de la médiane pour un triangle rectangle