Théorème de Stewart

Théorème de Stewart
Théorème de Stewart

En géométrie euclidienne, le théorème de Stewart est une généralisation du théorème de la médiane due au mathématicien Matthew Stewart dans les années 1746.

Enoncé

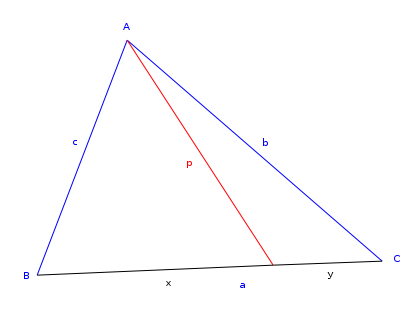
Théorème — Soit p une cévienne d'un triangle ABC divisant en X le côté a en deux parties x et y. On a alors la relation suivante :

a\cdot (xy+p^{2}) = x\cdot b^{2}+y\cdot c^{2}

Démonstration

D'après le théorème d'Al-Kashi nous avons :

\cos(\widehat{BXA})=\frac{x^{2}+p^{2}-c^{2}}{2xp}
\cos(\widehat{CXA)}=\frac{y^{2}+p^{2}-b^{2}}{2yp}

Puisque \widehat{BXA} et \widehat{CXA} sont supplémentaires, alors la somme de leur cosinus est nulle, d'où après somme nous obtenons :

\cos(\widehat{BXA})+ \cos(\widehat{CXA)}=\frac{x^{2}+p^{2}-c^{2}}{2xp}+\frac{y^{2}+p^{2}-b^{2}}{2yp}

\Leftrightarrow0=2yp\cdot(x^{2}+p^{2}-c^{2})+2xp\cdot(y^{2}+p^{2}-b^{2})

\Leftrightarrow2ypx^{2}+2yp^{3}+2xpy^{2}+2xp^{3}=2ypc^{2}+2xpb^{2}

\Leftrightarrow x^{2}y+yp^{2}+xy^{2}+xp^{2}=yc^{2}+xb^{2}

\Leftrightarrow a\cdot(xy+p^{2})=yc^{2}+xb^{2}

Voir aussi



Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Stewart de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Theoreme de Stewart — Théorème de Stewart Théorème de Stewart En géométrie euclidienne, le théorème de Stewart est une généralisation du théorème de la médiane due au mathématicien Matthew Stewart dans les années 1746. Enoncé Théorème …   Wikipédia en Français

  • Théorème de stewart — En géométrie euclidienne, le théorème de Stewart est une généralisation du théorème de la médiane due au mathématicien Matthew Stewart dans les années 1746. Enoncé Théorème …   Wikipédia en Français

  • Theoreme de la mediane — Théorème de la médiane Le théorème de la médiane, ou théorème d Apollonius, est une relation entre la longueur d une médiane d un triangle et la longueur de ses côtés. Il existe plusieurs versions de ce théorème dont certaines font appel au… …   Wikipédia en Français

  • Théorème d'Apollonius — Théorème de la médiane Le théorème de la médiane, ou théorème d Apollonius, est une relation entre la longueur d une médiane d un triangle et la longueur de ses côtés. Il existe plusieurs versions de ce théorème dont certaines font appel au… …   Wikipédia en Français

  • Stewart — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sommaire 1 Toponymes 2 Personnes 2.1 A C …   Wikipédia en Français

  • Théorème de la médiane — Le théorème de la médiane, ou théorème d Apollonius, est une relation entre la longueur d une médiane d un triangle et la longueur de ses côtés. Il existe plusieurs versions de ce théorème dont certaines font appel au produit scalaire. Enfin, il… …   Wikipédia en Français

  • Théorème CPT — Symétrie CPT La symétrie CPT est une symétrie des lois physiques pour les transformations impliquant de manière simultanée la charge, la parité et le temps. Sommaire 1 Historique et théorème CPT 2 Argument de démonstration …   Wikipédia en Français

  • Théorème de Bernoulli — Pour les articles homonymes, voir Loi de Bernoulli. Le théorème de Bernoulli qui a été établi en 1738 par Daniel Bernoulli exprime le bilan hydraulique simplifié d un fluide dans une conduite. Il a posé les bases de l hydrodynamique et, d une… …   Wikipédia en Français

  • Théorème de Wallace-Bolyai-Gerwien — En géométrie, le théorème de Lowry Wallace Bolyai Gerwien (ou encore théorème de Bolyai, théorème de Bolyai Gerwien ou théorème de Lowry Wallace Bolyai Gerwien) énonce que, lorsque deux polygones ont même aire, on peut découper le premier en un… …   Wikipédia en Français

  • Matthew Stewart (mathematicien) — Matthew Stewart (mathématicien) Pour les articles homonymes, voir Stewart. Matthew Stewart était un mathématicien écossais, né le 15 janvier 1717 à Rothesay (île de Bute), mort le 23 janvier 1785 à Catrine (Ayrshire) (mort à… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”