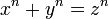Théorème de Wiles

Travail de Diophante traduit du grec en latin par Claude-Gaspard Bachet de Méziriac. Cette édition du livre a été publiée en 1621. La page 85 contient le problème II.VIII de Diophante, et est la page sur laquelle Pierre de Fermat écrivit que la marge était trop petite pour contenir la démonstration.

Andrew Wiles

En mathématiques, le dernier théorème de Fermat, ou théorème de Fermat-Wiles, énonce qu'il n'y a pas de nombres entiers non nuls x, y et z tels que:

dès que n est un entier strictement supérieur à 2.

Pour les valeurs de n inférieures ou égales à 2, il existe une infinité de solutions. Le cas n = 1 est évident. Le cas n = 2 admet notamment la solution classique 3² + 4² = 5². De manière générale, toutes les solutions pour n = 2 sont données par : x=2kml, y=k(m²-l²), z=k(m²+l²), où les nombres k, l et m satisfont les conditions: k entier, m>l, m et l de parités différentes. On appelle parfois ces entiers les triplets pythagoriciens. Cependant, dès que n est supérieur à deux, ce n'est plus possible.

Le théorème doit son nom à Pierre de Fermat qui écrivit en marge d'une traduction de l'Arithmetica de Diophante, à côté de l'énoncé de ce problème :

« 

J’ai trouvé une merveilleuse démonstration de cette proposition, mais la marge est trop étroite pour la contenir.

 »

Cette note sibylline laissait penser qu'une démonstration élémentaire était possible ; ce qui a donc vivement émoustillé la curiosité des gens. Après avoir été l'objet de fiévreuses recherches pendant plus de 300 ans, le théorème a finalement été démontré en 1994 par le mathématicien Andrew Wiles. La plupart des mathématiciens pensent aujourd'hui que Fermat s'était trompé en pensant avoir correctement démontré sa conjecture : la preuve connue (affinée depuis) fait appel à des outils très puissants de théorie des nombres.

Plus précisément, Wiles a prouvé un cas particulier de la conjecture de Shimura-Taniyama-Weil, dont on savait depuis quelque temps déjà, via les travaux de Yves Hellegouarch, Gerhard Frey, Jean-Pierre Serre et Ken Ribet, qu'elle impliquait le théorème. La preuve fait appel aux formes modulaires, aux représentations galoisiennes, à la cohomologie galoisienne, aux représentations automorphes, à la formule des traces…

Méthode de la démonstration

La démonstration d'Andrew Wiles s'appuie sur de nombreux travaux antérieurs et peut se résumer comme suit :

1. Associer aux solutions de l'équation de Fermat une courbe elliptique particulière (Frey, reprenant des idées d'Hellegouarch),
2. Démontrer que la courbe de Frey-Hellegouarch ne peut pas être paramétrée par des fonctions modulaires (Ribet, démontrant une conjecture de Serre),
3. Démontrer que toute courbe elliptique – ou une classe suffisamment importante pour contenir celle de Frey-Hellegouarch – est paramétrée par des fonctions modulaires : C'est la conjecture de Shimura-Taniyama-Weil, si importante en théorie des nombres.

La contradiction qui en résulte montre que l'équation de Fermat ne peut avoir de solutions.

Les courbes elliptiques

Une courbe elliptique est une courbe d'équation de la forme :

y² + axy + by = x³ + cx² + dx + e

Les coefficients a, b, c, d et e sont des éléments du corps sur lequel est définie la courbe. Pour qu'une telle courbe soit effectivement une courbe elliptique, il faut que la courbe ainsi définie ne soit pas singulière, c’est-à-dire qu'elle n'ait ni point de rebroussement, ni point double. Cette dernière condition s'exprime par le fait qu'un certain polynôme sur les coefficients, analogue à un discriminant, ne s'annule pas.

Si l'on prend l'exemple du corps des réels, alors l'équation d'une courbe elliptique définie sur le corps des nombres réels peut être mise sous une forme plus simple (dite équation de Weierstrass) :

y² = x³ + ax + b.

Le discriminant de cette courbe est δ = − 16(4a³ + 27b²). S'il est non nul, la courbe est non-singulière, et donc est vraiment une courbe elliptique.

La courbe de Frey-Hellegouarch

En 1984, Gerhard Frey, en reprenant des idées plus anciennes de Yves Hellegouarch, démontra que les solutions de l'équation de Fermat pour n > 2, permettaient de définir des courbes elliptiques semi-stables aux propriétés étranges ; ce sont les courbes d'équation :

y² = x(x + Aⁿ)(x − Bⁿ),

où Aⁿ + Bⁿ = Cⁿ est un contrexemple au théorème de Fermat.

Pour conclure, il suffit de montrer que la courbe elliptique ainsi définie a des propriétés trop bizarres pour pouvoir exister.

Comme dans d'autres situations en mathématiques, le fait d'intégrer le problème de Fermat dans un cadre apparemment beaucoup plus difficile constitue quand même une avancée, parce qu'on dispose alors de tout un outillage développé pour ce cadre.

La démonstration de Kenneth Ribet

En 1986, après pratiquement deux ans d'effort, l'Américain Kenneth Ribet réussit à démontrer une grande partie de la conjecture epsilon de Jean-Pierre Serre, dont une des conséquences est que la courbe de Frey-Hellegouarch n'est pas paramétrable par des fonctions modulaires.

Il ne restait plus qu'à démontrer la conjecture de Shimura-Taniyama-Weil : « Toute courbe elliptique est paramétrable par des fonctions modulaires ».

Conjecture de Shimura-Taniyama-Weil

La conjecture de Shimura-Taniyama-Weil précise que les courbes elliptiques peuvent toujours être associées (ou paramétrées ou dérivent) à des fonctions spéciales dites modulaires (généralisation des fonctions trigonométriques).

Pour démontrer cette conjecture, Andrew Wiles utilisa les notions mathématiques suivantes :

• Les fonctions L ;
• Les formes modulaires ;
• Les groupes de Galois absolus.

La démonstration complète a été publiée en 1995 dans Annals of Mathematics.

Remarques

Ce théorème n'a aucune application en soi : c'est par les idées qu'il a fallu mettre en œuvre pour le démontrer, par les outils qui ont été mis en place pour ce faire, qu'il prend une telle valeur. L'article Démonstrations du dernier théorème de Fermat montre quelques exemples d'outils découverts et utilisés pour la résolution de ce problème.

On peut également comprendre ce théorème graphiquement en considérant la courbe d'équation : xⁿ + yⁿ = 1. Si n > 2, alors cette courbe ne passe par aucun point à coordonnées rationnelles non nulles.

L'usage voulant qu'on donne à un théorème le nom de celui qui en a apporté la démonstration, l'appellation de « théorème de Fermat » ne se justifie pas à proprement parler. Il faudrait parler soit d'une « conjecture de Fermat », soit du « théorème de Wiles ».

Ce théorème n'a pas vraiment de relation avec le théorème de Pythagore. L'objet du théorème de Pythagore est de donner une caractérisation géométrique des triangles pythagoriciens, c'est-à-dire dont les longueurs des côtés forment un triplet pythagoricien, ces triplets étant eux-mêmes les solutions de l'équation de Fermat dans le cas n = 2. L'analogie avec le théorème de Fermat est donc la question de l'existence de triplets pythagoriciens, et la question de leur interprétation géométrique est nettement une autre question. Néanmoins, Fermat s'est évidemment inspiré de la notion de triplet pythagoricien : sa conjecture est en effet notée en marge d'un exposé de Diophante sur les triplets pythagoriciens.

Bibliographie

• Etude du théorème et de son histoire
• Wiles, Andrew (1995). Modular elliptic curves and Fermat's last theorem, Annals of Mathematics (141) (3), 443-551
• Simon Singh, Le Dernier Théorème de Fermat, (ISBN 2012789218)
  Un livre de vulgarisation qui prend le dernier théorème de Fermat pour présenter la théorie des nombres.
• Un documentaire télévisé de vulgarisation de ce même Simon Singh
• Yves Hellegouarch, Invitation aux mathématiques de Fermat-Wiles [détail des éditions]
• Guillermo Martínez, Mathématique du crime

Articles connexes

• Démonstrations du dernier théorème de Fermat

• Portail des mathématiques