- Théorème de Lagrange (algèbre)
-
Théorème de Lagrange sur les groupes
Pour les articles homonymes, voir Théorème de Lagrange.
Joseph-Louis Lagrange
En mathématiques, et plus particulièrement en théorie des groupes, le théorème de Lagrange est un théorème qui énonce un résultat élémentaire fournissant des informations combinatoires sur les groupes finis. Il est nommé ainsi en l'honneur du mathématicien Joseph-Louis Lagrange.
Sommaire
Énoncé
Théorème de Lagrange — Pour un groupe G fini, et pour tout sous-groupe H de G, le cardinal (encore appelé ordre) de H divise le cardinal de G :
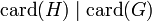.Le quotient du cardinal de G par le cardinal de H s'appelle l'indice de H dans G et il est noté [G:H] :
![\mbox{card}(G)= \mbox{card} (H)\times[G:H]\,](/pictures/frwiki/101/ebb44634047dd337525d0851e2248753.png)
.Démonstrations
La première démonstration est la démonstration classique, relativement élémentaire. La seconde s'appuie sur la notion d'action de groupe dont la définition est rappelée.
Relation d'équivalence
La première preuve du théorème consiste à partitionner l'ensemble G en une famille d'ensembles équipotents à H (autrement dit, de même cardinal que H). La donnée d'une partition équivaut à la donnée d'une relation d'équivalence sur G.
Soit
la relation binaire sur G définie par :
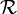vérifie les propriétés suivantes :- Réflexivité : Par définition de l'inverse, tout élément x dans G vérifie l'identité
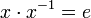. L'élément neutre e appartient à H par définition d'un sous-groupe. De fait, 
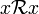. - Symétrie : Pour tous x et y dans G, on écrit :
.
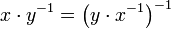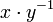appartient à H si et seulement si 
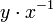appartient à H ; équivalence qui se réécrit : 
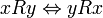. - Transitivité : Pour tous x,y,z dans G, l'associativité du produit donne :
.
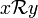et 
, alors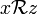 
.
La relation
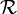est réflexive, symétrique, et transitive, donc elle définit une relation d'équivalence sur l'ensemble G. La classe d'équivalence de e n'est autre que H.Remarquons que la relation
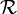est G-invariante à droite : pour tous x,y et z dans G, 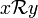implique (donc, est équivalent à) 
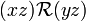. En particulier, lorsque C désigne une classe d'équivalence, et x un élément de C, alors l'ensemble 
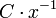est la classe d'équivalence de e, donc H. En effet, C=Hx (y dans C <=> xRy <=> il existe h dans H tel que 
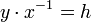<=>y dans Hx), donc 
.Comme l'application
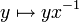est une bijection, les ensembles C et H ont même cardinal. De suite, les classes d'équivalence partitionnent G en des parties de même cardinal que H.Action de groupe
Article détaillé : action de groupe (mathématiques).Une action d'un groupe fini G sur un ensemble X est la donnée pour tout élément g de G d'une application bijective
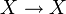envoyant x sur un élément noté 
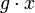, vérifiant les deux conditions suivantes :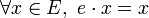
Si le groupe fini G agit sur un ensemble X, le stabilisateur d'un point x de X est défini comme l'ensemble des éléments h du groupe G tels que
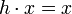; il est facile de vérifier que les stabilisateurs sont des sous-groupes de G. L'orbite de x se définit comme l'ensemble des éléments y de X s'écrivant : 
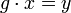pour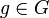 
. La conjugaison par l'élément g induit une bijection du stabilisateur de x sur le stabilisateur de :
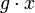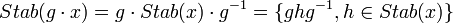.En particulier, le cardinal du stabilisateur de x ne dépend pas du choix de x dans son orbite. Par application du lemme des bergers, le cardinal du stabilisateur de x divise le cardinal de G, et le quotient est égal au cardinal de l'orbite de x.
La preuve du théorème de Lagrange consiste à réaliser tout sous-groupe H d'un groupe fini G comme un stabilisateur pour une action de G. L'action considérée est l'action du groupe G par translation à gauche sur l'ensemble X de ses parties, définie comme suit :
.Le stabilisateur d'un sous-groupe H est précisément H. En effet, l'égalité gH = H implique l'existence d'un élément h vérifiant gh = 1 ; autrement dit, g doit être l'inverse d'un élément de H, et a fortiori doit appartenir lui même à H. Réciproquement, comme le produit d'éléments de H appartient à H, tout élément h de H vérifie
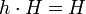. De fait, par double inclusion, H est le stabilisateur de H et la propriété s'en trouve démontrée.Historique
Le mathématicien français Joseph-Louis Lagrange a démontré que, par permutation des n indéterminées d'une expression polynômiale, le nombre d'expressions obtenues est un diviseur de n!. L'ensemble des permutations est vu aujourd'hui comme un groupe à n! éléments, agissant sur les polynômes à n variables. Le travail de Lagrange se réinterprète comme le calcul du cardinal d'une orbite de cette action : il apparait comme précurseur des recherches sur les groupes, dont les premiers termes de vocabulaires furent introduits suite aux travaux d'Augustin Louis Cauchy[1], et dont la définition formelle n'a été donnée qu'en 1882 par Walther Franz Anton von Dyck.
Applications courantes
- L'ordre d'un élément x d'un groupe fini se définit comme le cardinal du sous-groupe qu'il engendre. C'est le plus petit entier naturel n vérifiant : xn = e. Il divise l'ordre du groupe.
- Un groupe G d'ordre premier p est cyclique. En effet, tout élément non nul x de G est d'ordre strictement supérieur à 1 et par ce qui précède un diviseur de p. Comme p est premier, l'ordre de x est p ; autrement dit, x engendre un groupe cyclique d'ordre p, nécessairement égal à G.
- Ce théorème peut servir à démontrer le petit théorème de Fermat.
Notes et références
- ↑ Bruno Belhoste, Cauchy, un mathématicien légitimiste au XIXe siècle [détail des éditions]
Portail des mathématiques
Catégories : Théorème de mathématiques | Théorie des groupes | Joseph-Louis Lagrange | Groupe fini - Réflexivité : Par définition de l'inverse, tout élément x dans G vérifie l'identité
Wikimedia Foundation. 2010.
