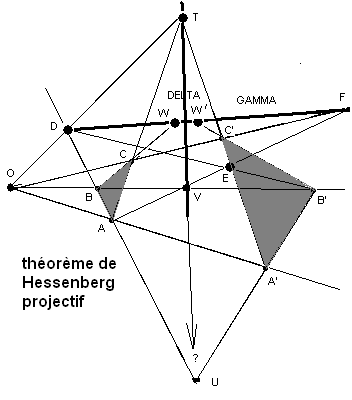
Théorème de Hessenberg

Théorème de Hessenberg

Théorème d'Hessenberg

En géométrie projective, le théorème d’Hessenberg fait le lien entre le théorème de Pappus et le théorème de Desargues.

On s’intéresse ici au théorème d'Hessenberg dans sa version projective (il existe également une version affine qui s'en déduit aisément).

Énoncé succinct

Un plan projectif de Pappus (PPP) est arguésien (PPA).

Énoncé moins ésotérique

Étant donnés deux triangles ABC et A'B'C', si (AA'), (BB') et (CC') sont concourantes (en O) alors les 3 points d'intersection des côtés homologues des triangles ((AB) ∩ (A'B'), (AC) ∩ (A'C') et (BC) ∩ (BC')) sont alignés.

Démonstration

Une démonstration possible, n'ayant pas besoin du théorème fondamental de la géométrie projective, ne nécessite seulement que la création de points d'intersection supplémentaires et l'emploi à trois reprises de l'axiome de Pappus.

Nous avons deux triangles ABC et A'B'C' en perspective depuis le point O. Nous définissons des points auxiliaires :

T = (AC) ∩ (A'C') ; U = (AB) ∩ (A'B') ; D = (AB) ∩ (OT) ; E = (DB') ∩ (A'C') ; F = (EA) ∩ (OC') et V = (EA) ∩ (OB'),

ainsi que des droites auxiliaires :

Γ = (DF) et Δ = (TV).

Le but est de montrer que U est sur Δ et que les points W = (BC) ∩ Γ et W' = (B'C') ∩ Γ sont confondus. Hessenberg.PNG

On applique l’axiome de Pappus aux alignements :

  • OAA' et EB'D ce qui donne T, V, U alignés (sur Δ = (TV) par conséquent)
  • OFC et ABD ce qui donne T, V, W alignés (sur Δ par conséquent)
  • OFC' et EB'D ce qui donne T, V, W' alignés (sur Δ par conséquent)

Il s'ensuit que W et W' sont à la fois sur Δ et Γ, donc sont un point unique (un axiome des PPI).

Ainsi T, U et W sont sur Δ. Or nous avions défini W sur (BC) et W' sur (B'C'), donc W = (BC) ∩ (B'C').

Nous avons bien démontré le théorème d’Hessenberg i.e. que les intersections respectives de (AB), (BC) et (CA) avec (A'B'), (B'C') et (C'A') sont alignées. C.Q.F.D.


Articles de Géométrie projective ou voisins à consulter. [modifier]
Hexagramme de Pascal • Axiomes de plans projectifs • Théorème de Pappus • Théorème de Desargues • Dualité • Axiomes de plans projectifs/Suite des axiomes  • Axiomes de plans projectifs/homogènes • Axiomes de plans projectifs/barycentriques • Plan affine • Théorème d'Hessenberg • Traité projectif des coniques • Traité projectif des coniques/Dans un plan pappusien • Conique • Octonions • Relation d'équivalence • Structure de corps • Construction d'un cercle point par point • Construction d'une parabole tangente par tangente • Plan de Fano • Portail:Géométrie • Géométrie analytique • Géométrie synthétique • Géométrie • Géométrie projective • Géométrie non euclidienne • Division harmonique • Rapport anharmonique • Application projective • Fonction homographique • Perspective • Perspective conique • Infini • Droite (mathématiques) 
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Th%C3%A9or%C3%A8me d%27Hessenberg ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Hessenberg de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Theoreme d'Hessenberg — Théorème d Hessenberg En géométrie projective, le théorème d’Hessenberg fait le lien entre le théorème de Pappus et le théorème de Desargues. On s’intéresse ici au théorème d Hessenberg dans sa version projective (il existe également une version… …   Wikipédia en Français

  • Théorème d'Hessenberg — En géométrie projective, le théorème d’Hessenberg fait le lien entre le théorème de Pappus et le théorème de Desargues. On s’intéresse ici au théorème d Hessenberg dans sa version projective (il existe également une version affine qui s en déduit …   Wikipédia en Français

  • Théorème d’Hessenberg — Théorème d Hessenberg En géométrie projective, le théorème d’Hessenberg fait le lien entre le théorème de Pappus et le théorème de Desargues. On s’intéresse ici au théorème d Hessenberg dans sa version projective (il existe également une version… …   Wikipédia en Français

  • Théorème de Hessenberg (géométrie) —  En théorie des ensembles le théorème de Hessenberg désigne parfois l énoncé que le carré d un aleph est égal à lui même, ou (avec axiome du choix) le même énoncé pour un cardinal infini. Dans une approche axiomatique de la géométrie… …   Wikipédia en Français

  • HESSENBERG — Théorème d Hessenberg En géométrie projective, le théorème d’Hessenberg fait le lien entre le théorème de Pappus et le théorème de Desargues. On s’intéresse ici au théorème d Hessenberg dans sa version projective (il existe également une version… …   Wikipédia en Français

  • Théorème de Desargues — dans un plan projectif : les deux triangles (non plats) ABC et A B C ont leurs sommets sur 3 droites distinctes p = (AA ) , q = (BB ) et r = (CC ) ; alors ces 3 droites sont concourantes (en S) si et seulement si les points P = (BC) ∩… …   Wikipédia en Français

  • Theoreme de Pappus — Théorème de Pappus Sommaire 1 Introduction 2 Énoncé du théorème 3 Démonstration à l aide des applications projectives 4 Notions connexes …   Wikipédia en Français

  • Théorème de pappus — Sommaire 1 Introduction 2 Énoncé du théorème 3 Démonstration à l aide des applications projectives 4 Notions connexes …   Wikipédia en Français

  • Theoreme de Desargues — Théorème de Desargues Le théorème de Desargues est l un des (sinon le) plus important théorème de la géométrie projective. Il lie deux triangles et les droites qu ils déterminent. Il est lié à la notion de groupes harmoniques. Sommaire 1 En… …   Wikipédia en Français

  • Théorème de desargues — Le théorème de Desargues est l un des (sinon le) plus important théorème de la géométrie projective. Il lie deux triangles et les droites qu ils déterminent. Il est lié à la notion de groupes harmoniques. Sommaire 1 En géométrie projective 2 En… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”