Théorème de Hessenberg (géométrie)

Théorème de Hessenberg (géométrie)
Page d'aide sur l'homonymie En théorie des ensembles le théorème de Hessenberg désigne parfois l'énoncé que le carré d'un aleph est égal à lui-même, ou (avec axiome du choix) le même énoncé pour un cardinal infini.

Dans une approche axiomatique de la géométrie projective ou de la géométrie affine, le théorème de Hessenberg montre que le théorème de Desargues se déduit du théorème de Pappus, pris comme axiome en plus des axiomes d'incidence. Ce théorème a été démontré par Gerhard Hessenberg en 1905.

Énoncé (dans le cas projectif)

Ce théorème énonce qu'un plan projectif de Pappus est arguésien. De façon plus détaillée :

Théorème de Hessenberg. — Dans un plan projectif satisfaisant les axiomes d'incidence et la propriété de Pappus, la propriété de Desargues est vérifiée, à savoir que, étant donnés deux triangles ABC et A'B'C', si (AA'), (BB') et (CC') sont concourantes alors les 3 points d'intersection des côtés homologues des triangles, soit (AB) ∩ (A'B'), (AC) ∩ (A'C') et (BC) ∩ (BC'), sont alignés.

Théorème de Desargues : si les deux triangles (non plats) ABC et A'B'C' ont leurs sommets sur 3 droites distinctes (AA') , (BB') et (CC') concourantes en S, alors les points P = (BC) ∩ (B'C'), Q = (AC) ∩ (A'C') et R = (AB) ∩ (A'B') sont alignés.

Démonstration

Pour le démontrer, il suffit de considérer quelques points d'intersection supplémentaires et d'employer (à trois reprises) l'axiome de Pappus.

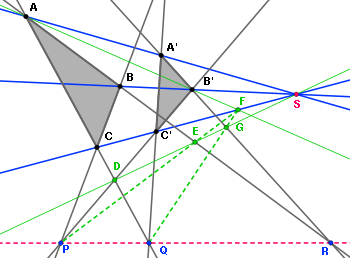
Les deux triangles ABC et A'B'C' sont en perspective depuis le point S, et leurs côtés homologues s'intersectent en

P = (BC) ∩ (B'C'), Q = (AC) ∩ (A'C') et S = (AB) ∩ (A'B')

et on veut montrer que ces 3 points sont alignés.

  1. Soit le point D = (AC) ∩ (B'C'). La propriété de Pappus pour les deux triplets de points alignés (S,B',B) et (A,C,D) donne, en posant E = (SD) ∩ (AB) et F = (SC) ∩ (B'A), que P (= (B'D) ∩ (CB) ), F et E sont alignés.
  2. La propriété de Pappus pour les deux triplets de points alignés (S,A,A') et (B',C',D) donne, en posant G = (SD) ∩ (B'A'), que Q (= AD) ∩ (C'A') ), G et F (= (SC') ∩ (B'A) ) sont alignés.
  3. La propriété de Pappus pour les deux triplets de points alignés (A,B',F) et (G,E,D) donne que P (sur (EF) d'après 1), Q (sur (GF) d'après 2), et R sont alignés, ce qui est le résultat cherché.

Bibliographie

  • (en) H.S.M. Coxeter, Introduction to Geometry [détail des éditions] p. 238-239 (démonstration dans le cas projectif).
  • Jacqueline Lelong-Ferrand, Fondements de la géométrie, PUF, 1985 (ISBN 2-13-038851-5)  p. 187 (démonstration dans le cas affine).

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Hessenberg (géométrie) de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Theoreme d'Hessenberg — Théorème d Hessenberg En géométrie projective, le théorème d’Hessenberg fait le lien entre le théorème de Pappus et le théorème de Desargues. On s’intéresse ici au théorème d Hessenberg dans sa version projective (il existe également une version… …   Wikipédia en Français

  • Théorème d'Hessenberg — En géométrie projective, le théorème d’Hessenberg fait le lien entre le théorème de Pappus et le théorème de Desargues. On s’intéresse ici au théorème d Hessenberg dans sa version projective (il existe également une version affine qui s en déduit …   Wikipédia en Français

  • Théorème de Hessenberg — Théorème d Hessenberg En géométrie projective, le théorème d’Hessenberg fait le lien entre le théorème de Pappus et le théorème de Desargues. On s’intéresse ici au théorème d Hessenberg dans sa version projective (il existe également une version… …   Wikipédia en Français

  • Théorème d’Hessenberg — Théorème d Hessenberg En géométrie projective, le théorème d’Hessenberg fait le lien entre le théorème de Pappus et le théorème de Desargues. On s’intéresse ici au théorème d Hessenberg dans sa version projective (il existe également une version… …   Wikipédia en Français

  • Théorème de Desargues — dans un plan projectif : les deux triangles (non plats) ABC et A B C ont leurs sommets sur 3 droites distinctes p = (AA ) , q = (BB ) et r = (CC ) ; alors ces 3 droites sont concourantes (en S) si et seulement si les points P = (BC) ∩… …   Wikipédia en Français

  • HESSENBERG — Théorème d Hessenberg En géométrie projective, le théorème d’Hessenberg fait le lien entre le théorème de Pappus et le théorème de Desargues. On s’intéresse ici au théorème d Hessenberg dans sa version projective (il existe également une version… …   Wikipédia en Français

  • Theoreme de Pappus — Théorème de Pappus Sommaire 1 Introduction 2 Énoncé du théorème 3 Démonstration à l aide des applications projectives 4 Notions connexes …   Wikipédia en Français

  • Théorème de pappus — Sommaire 1 Introduction 2 Énoncé du théorème 3 Démonstration à l aide des applications projectives 4 Notions connexes …   Wikipédia en Français

  • Theoreme de Desargues — Théorème de Desargues Le théorème de Desargues est l un des (sinon le) plus important théorème de la géométrie projective. Il lie deux triangles et les droites qu ils déterminent. Il est lié à la notion de groupes harmoniques. Sommaire 1 En… …   Wikipédia en Français

  • Théorème de desargues — Le théorème de Desargues est l un des (sinon le) plus important théorème de la géométrie projective. Il lie deux triangles et les droites qu ils déterminent. Il est lié à la notion de groupes harmoniques. Sommaire 1 En géométrie projective 2 En… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”