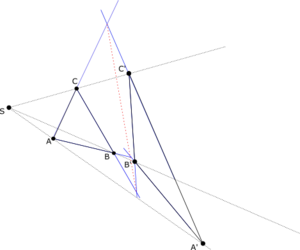- Théorème de desargues
-
Théorème de Desargues
Le théorème de Desargues est l'un des (sinon le) plus important théorème de la géométrie projective. Il lie deux triangles et les droites qu'ils déterminent. Il est lié à la notion de groupes harmoniques.
Sommaire
En géométrie projective
En géométrie projective, son énoncé est le suivant :
Soient ABC et A'B'C' deux triangles sans point commun tels que les droites (AA'), (BB') (CC') soient concourantes. Alors, les points d'intersection des droites
- (AB) et (A'B')
- (AC) et (A'C')
- (BC) et (B'C')
sont situés sur une même droite.
Dans le cas où aucun point d'intersection n'est un point impropre, on obtient la configuration ci-contre:
Le dual de ce théorème en donne aussi la réciproque :
- ABC et A'B'C' deux triangles sans point commun tels que les points d'intersection des droites
- (AB) et (A'B')
- (AC) et (A'C')
- (BC) et (B'C')
- sont situés sur une même droite
- alors les droites (AA'), (BB') (CC') sont concourantes (en un point propre ou impropre).
En géométrie projective, une démonstration simple consiste à utiliser une application projective qui transforme les triangles (ABC) et (A'B'C') en (A1B1C1) et (A'1B'1C'1) de telle sorte que les points d'intersection de (A1B1) et (A'1B'1) et de (A1C1) et (A'1C'1) soient impropres. Les droites (A1B1) et (A'1B'1) sont alors parallèles ainsi que les droites (A1C1) et (A'1C'1). On est alors revenu à la configuration précédente qui prouve que (B1C1) et (B'1C'1) sont parallèles et que leur point d'intersection est donc impropre (situé sur la même droite que les deux précédents). On en déduit alors la propriété sur les droites de départ.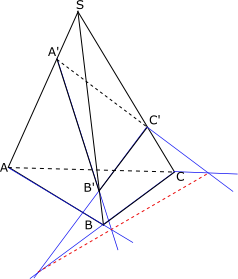 Desargues et perspective
Desargues et perspective
En géométrie "classique", cette forme du théorème de Desargues peut se démontrer en imaginant que notre dessin représente en perspective un tetraèdre SABC coupé par un plan (A'B'C'). Les droites (AB) et (A'B') étant dans le plan (SAB) leur point d'intersection apparent est un point d'intersection réel commun au deux plans (ABC) et (A'B'C'), il en est de même du point d'intersection des droites (BC) et (B'C') et du point d'intersection des droites (AC) et (A'C'). Les plans (ABC) et (A'B'C') sont sécants suivant une droite (d) qui contient ces trois points d'intersection.
En géométrie affine
En géométrie affine, le théorème de Desargues doit être complété pour prendre en compte les cas particuliers dus au parallélisme. La géométrie arguésienne permet de faire apparaitre ces énoncés particuliers comme des corollaires du cas général :
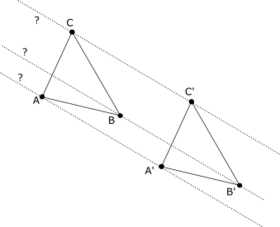
Si ABC et A'B'C' sont deux triangles, sans point commun tels que
- (AB) //(A'B')
- (BC) // (B'C')
- (CA)// (C'A')
alors les droites (AA'), (BB') et (CC') sont concourantes ou parallèles.
Dans la première configuration, on suppose que deux des droites (par exemple (AA') et (BB')) sont sécantes en S. La preuve s'effectue en construisant le point M sur (SC) tel que (A'M)//(AC). Le théorème de Thalès permet de prouver qu'alors (MB')//(CB). Or il n'existe qu'un seul point situé, d'une part sur la parallèle à (AC) menée par A', d'autre part sur la parallèle à (BC) menée par B' et ce point est C'. Donc M et C' sont confondus et les points SCC' sont donc alignés.Dans la seconde configuration, on ne trouve aucune droite sécante : elles sont donc parallèles.
Réciproque : Soient ABC et A'B'C' deux triangles sans point commun tels que
- les droites (AA'), (BB') et (CC') sont concourantes ou parallèles
- (AB)//(A'B')
- (AC)//(A'C')
alors (BC)//(B'C').
Avec des droites concourantes, nous retrouvons une conséquence du théorème de Thalès. Avec des droites parallèles, la démonstration utilise l'existence des parallélogramme (AA'B'B) et (AA'C'C) pour en déduire l'existence du parallélogramme (BB'C'C).Théorème de Desargues et définition axiomatique
Au début du XXme siècle, David Hilbert tente une définition axiomatique du plan affine. Sur un espace muni de points, il définit des droites comme des ensembles de points vérifiant certains axiomes dont
- Par deux points distincts passe une et une seule droite.
- Toute droite contient au moins deux points. Il existe au moins trois points non alignés.
- Par un point A extérieur à une droite (d) , il ne passe qu'une seule droite parallèle à (d) (parallèle i. e. n'a pas de point commun avec).
Il découvre alors que ces axiomes ne permettent pas de démontrer le théorème de Desargues. Il faut l'existence de l'espace ou de l'axiome de la congruence. En d'autres termes, cet énoncé a valeur d'axiome en géométrie (affine ou projective) plane.
En 1902, Moulton exhibe un exemple de plan — le plan de Moulton — vérifiant les trois axiomes précédents et dans lequel le théorème de Desargues est faux.
Liens
- Girard Desargues, sa vie, son oeuvre.
- Le Théorème d'Hessenberg qui fait le lien entre le théorème de Pappus et le présent théorème de Desargues.
- La géométrie arguésienne permet de faire le lien entre les deux versions de ce théorème.
Articles de Géométrie projective ou voisins à consulter. [modifier] Hexagramme de Pascal • Axiomes de plans projectifs • Théorème de Pappus • Théorème de Desargues • Dualité • Axiomes de plans projectifs/Suite des axiomes • Axiomes de plans projectifs/homogènes • Axiomes de plans projectifs/barycentriques • Plan affine • Théorème d'Hessenberg • Traité projectif des coniques • Traité projectif des coniques/Dans un plan pappusien • Conique • Octonions • Relation d'équivalence • Structure de corps • Construction d'un cercle point par point • Construction d'une parabole tangente par tangente • Plan de Fano • Portail:Géométrie • Géométrie analytique • Géométrie synthétique • Géométrie • Géométrie projective • Géométrie non euclidienne • Division harmonique • Rapport anharmonique • Application projective • Fonction homographique • Perspective • Perspective conique • Infini • Droite (mathématiques) - Portail de la géométrie
Catégories : Géométrie projective | Théorème de mathématiques
Wikimedia Foundation. 2010.