Théorème d'Artin-Schreier

Théorème d'Artin-Schreier

Théorie d'Artin-Schreier

En mathématiques, la théorie d'Artin-Schreier donne une description des extensions galoisiennes de degré p d'un corps de caractéristique p. Elle traite donc un cas inaccessible à la théorie de Kummer.

Extension d'Artin-Schreier

Soit K un corps de caractéristique p, et a un élément de ce corps. Le corps de décomposition du polynôme Xp-X+a au-dessus de K, est appelé extension d'Artin-Schreier. Si b est une racine de ce polynôme, alors tous les b+i pour i allant de 0 à p-1 sont p-racines distinctes. 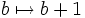Le corps de décomposition est donc séparable, K-engendré par b, et une extension cyclique de degré p de K, un générateur du groupe de Galois étant le morphisme défini par b\mapsto b+1.

Par exemple, le corps fini à deux éléments admet comme extension d'Artin-Schreier le corps fini à 4 éléments, engendrée par le polynôme X2-X+1=X2+X+1.

Théorie d'Artin-Schreier

La théorie d'Artin-Schreier consiste en une réciproque au fait ci-dessous : toute extension cyclique de degré p d'un corps de caractéristique p est une extension d'Artin-Schreier. Ceci se démontre par exemple en utilisant le théorème 90 de Hilbert sous sa version additive.

Les extensions de degré p non galoisiennes ne peuvent être décrites à l'aide de cette théorie. Par exemple, l'extension obtenue en ajoutant une racine p-ème de l'indéterminée T (c'est-à-dire une racine du polynôme en l'indéterminée X, Xp-T, qui est inséparable) dans le corps 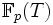\mathbb{F}_p(T) des fonctions à une variable au-dessus du corps premier à p éléments.

Une théorie analogue en caractéristique p à celle de la résolution par radicaux, doit donc autoriser des extensions d'Artin-Schreier. Pour obtenir des extensions d'ordre des puissances de la caractéristique, il faut utiliser la théorie des vecteurs de Witt.


  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9orie d%27Artin-Schreier ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème d'Artin-Schreier de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Theorie d'Artin-Schreier — Théorie d Artin Schreier En mathématiques, la théorie d Artin Schreier donne une description des extensions galoisiennes de degré p d un corps de caractéristique p. Elle traite donc un cas inaccessible à la théorie de Kummer. Extension d Artin… …   Wikipédia en Français

  • Théorie d'artin-schreier — En mathématiques, la théorie d Artin Schreier donne une description des extensions galoisiennes de degré p d un corps de caractéristique p. Elle traite donc un cas inaccessible à la théorie de Kummer. Extension d Artin Schreier Soit K un corps de …   Wikipédia en Français

  • Théorie d'Artin-Schreier — En mathématiques, la théorie d Artin Schreier (en) donne une description des extensions galoisiennes de degré p d un corps de caractéristique p. Elle traite donc un cas inaccessible à la théorie de Kummer. Extension d Artin Schreier Soit K… …   Wikipédia en Français

  • Emil Artin — Pour les articles homonymes, voir Artin. Emil Artin. Emil Artin (3 mars 1898 à Vienne, 20  …   Wikipédia en Français

  • ARTIN (E.) — On peut considérer Artin comme un des fondateurs de l’algèbre contemporaine; par exemple, de l’aveu de son auteur, le livre Moderne Algebra de Van der Waerden, qui fut l’ouvrage de référence pendant trente ans, est issu de leçons professées par… …   Encyclopédie Universelle

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… …   Wikipédia en Français

  • Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Corps réel clos — En mathématiques, un corps réel clos est un corps totalement ordonné F tel que tout élément positif soit un carré et que tout polynôme de degré impair à coefficients dans F ait au moins une racine dans F. Le corps des réels, le corps des réels… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”