- Automorphismes
-
Automorphisme
Un automorphisme est un isomorphisme d'un objet mathématique X dans lui-même. Autrement dit, c'est une bijection de X dans X qui préserve la « structure » de X. On peut le voir comme une symétrie de X.
Sommaire
Définition
La définition abstraite d'un automorphisme est la suivante : c'est un endomorphisme qui est en même temps un isomorphisme. Autrement dit, c'est un morphisme d'un objet X d'une catégorie donnée dans lui-même, qui est également un isomorphisme.
Cette définition est très générale et peut paraître assez abstraite. Dans les cas les plus fréquents cependant, elle se réduit à quelque chose de beaucoup plus concret. Par exemple, dans le cas d'une structure algébrique, un automorphisme sera simplement une application bijective qui préserve la ou les lois de composition définissant la structure.
L'ensemble des automorphismes d'un objet X est en général noté Aut(X), ou AutC(X) lorsqu'on veut préciser que l'on se place dans la catégorie C. La composition de fonctions (ou des flèches dans le cadre général des catégories) donne à Aut(X) une structure de groupe : l'élément neutre est la fonction identité, et l'inverse d'un automorphisme est sa réciproque.
Exemples
- Si X est un ensemble, les automorphismes de X sont les permutations de X dans lui-même. On appelle Aut(X) le groupe symétrique sur X.
- Si V est un espace vectoriel sur un corps K, les automorphismes de V sont les applications linéaires bijectives de V dans lui-même. Dans le cas où V est de dimension finie n, Aut(V) est isomorphe à GLn(K).
- Si X est un espace topologique, les automorphismes de X sont les homéomorphismes de X dans lui-même.
- Si M est une variété différentielle, les automorphismes de M sont les difféomorphismes de M dans elle-même.
- Si K est un corps, un automorphisme de K est simplement un morphisme d'anneau bijectif de K dans K. Par exemple,
n'a pas d'automorphismes non triviaux. Par contre, 
possède deux automorphismes continus : l'identité et la conjugaison. possède également d'autres automorphismes de corps non continus. L'étude des automorphismes de corps constitue l'objet principal de la théorie de Galois.
Automorphismes intérieurs et extérieurs
Article détaillé : Automorphisme intérieur.Si G est un groupe, les automorphismes de G sont les morphismes bijectifs de G dans G.
On peut remarquer que, si
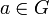, l'application 
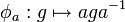est un automorphisme de G. L'application 
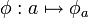est alors un morphisme de groupe de G vers Aut(G). En particulier, si le centre de G est trivial, G peut être vu comme un sous-groupe de Aut(G).Dans le cas général, on appelle intérieur un automorphisme de la forme φa. L'ensemble des automorphismes intérieurs (autrement dit, l'image de φ), est notée Int(G). C'est un sous-groupe normal de Aut(G). Le quotient de Aut(G) par Int(G) est noté Out(G), ce sont les automorphimes extérieurs de G.
Sous-groupe des automorphismes
- On peut parfois s'intéresser à un sous-groupe des automorphismes. L'un des premiers exemples marquant est celui d'un automorphisme de corps qui est l'identité sur un sous-corps. Concept qui a abouti à la théorie de Galois.
- Si l'on a un morphisme, f, de A dans B on peut s'intéresser aux automorphismes de A qui sont compatibles avec f. On obtient ainsi le concept de morphisme au-dessus d'un objet, concept très présent dans la géométrie algébrique. Si le morphisme f est un revêtement on retrouve la théorie de Galois liée aux revêtements.
Portail des mathématiques
Catégories : Algèbre générale | Théorie des catégories
Wikimedia Foundation. 2010.
