- Temperament mesotonique
-
Tempérament mésotonique
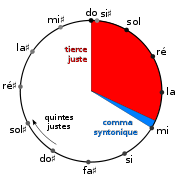
Acoustique musicale Gamme musicale Gammes et tempéraments Mesure des intervalles Un tempérament mésotonique est un tempérament musical construit à partir de la gamme pythagoricienne en diminuant toutes ses quintes justes d'une fraction du comma syntonique afin d'améliorer la justesse de ses tierces. En effet la tierce pythagoricienne ou diton (elle égale deux tons et son rapport de fréquences est 81/64) diffère de la tierce pure (rapport 5/4 ou 80/64) d'un intervalle appelé comma syntonique.
La modification de la gamme de Pythagore peut varier selon l'importance donnée à la pureté respective des tierces et des quintes. Il y a donc plusieurs tempéraments mésotoniques possibles selon l'équilibrage choisi, avec une éventualité extrême où on fait jouer aux quintes et aux tierces un rôle opposé à celui qu'elles jouent dans la gamme de Pythagore : toutes les tierces - sauf une - sont pures, et les quintes sont toutes légèrement fausses en conséquence.
L'adjectif « mésotonique » indique que tous les tons sont égaux à une valeur médiane (le préfixe méso vient du grec et signifie « au milieu »). A contrario, les gammes naturelles à tierces pures (comme celle de Zarlino) se divisent en tons majeurs (de rapport 9/8) et tons mineurs (de rapport 10/9), qui diffèrent entre eux d'un comma syntonique.
Sommaire
Définition
La gamme de Pythagore est exclusivement basée sur des quintes pures (de rapport 3/2) et ne tient pas compte de la tierce pure de rapport 5/4. Par comparaison, la tierce pythagoricienne a un rapport de 81/64 (contre 5/4 = 80/64) : la différence (81/80) est le comma syntonique.
En partant du cycle des quintes servant à la construction de la gamme pythagoricienne, on trouve 4 quintes dans l'intervalle de chaque tierce (par exemple do - mi contient les quintes do - sol, sol - ré, ré - la et la - mi). De la même façon, un ton contient deux quintes (par exemple le ton do - ré contient les quintes do - sol et sol - ré), ce qui donne exactement deux tons pour une tierce majeure.
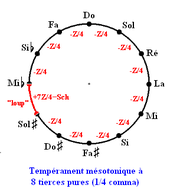
On peut rendre une tierce de cette gamme complètement pure tout en conservant égaux les deux tons qui la composent : en réduisant les 4 quintes correspondantes d'un quart de comma syntonique chacune. En appliquant le procédé à l'octave entière, ou plutôt aux 11 quintes justes (en laissant de côté la quinte du loup), on obtient le tempérament mésotonique à quart de comma.
Ce tempérament rend les tierces justes en faussant toutes les quintes. Au total, on a réduit l'intervalle des 12 quintes justes de presque 3 commas syntoniques : pour conserver une octave pure, la quinte du loup de la gamme pythagoricienne (égale à une quinte juste moins le comma pythagoricien) doit être complétée avec les 11/4 de commas syntoniques retirés. Les deux types de comma ayant une valeur assez proche, la quinte du loup dans ce tempérament mésotonique est plus grande qu'une quinte juste d'environ deux commas.
On peut alors imaginer de réduire les quintes d'une quantité moindre pour mieux équilibrer la répartition de la fausseté des intervalles, en divisant le comma par un autre chiffre situé de préférence entre 4 et 12. Les solutions les plus courantes sont celles à 1/6 et à 1/8 de comma. Le tempérament mésotonique au 1/12 de comma arrive à rendre la quinte du loup quasiment égale aux autres ; elle n'en diffère que de la différence entre commas pythagoricien et syntonique, que l'on appelle le schisma. Mais on peut aussi remarquer qu'on est tellement proche du tempérament égal que conserver ce schisma résiduel n'a pas de sens. Dans la pratique, ce tempérament équivaut au tempérament égal.
Calcul des intervalles tempérés
En notant « n » la fraction de comma syntonique utilisée, la correction appliquée à la quinte juste (pythagoricienne) est le facteur (80/81)1/n. (On se souvient que 80 = 24 x 5 et que 81 = 34)
La quinte tempérée (QT) vaut 3/2 x (80/81)1/n.
La « quinte du loup » (QL) vaut sept octaves diminuées de 11 quintes tempérées, soit 27/(3/2 x (80/81)11/n).
Prenons l'exemple du mésotonique à 1/4 de comma : QT) = 3/2 x (24 x 5 / 34)1/4.ou
QT) = 3/2 x '(2 x 51/4) / 3) ou
QT) = 51/4 c’est-à-dire
QT) = 1,4953...QL = 27 / 511/4 c’est-à-dire
QL = 1,5312....Comparaison des différents tempéraments mésotoniques
Fréquences des notes dans 6 systèmes, pour do = 264 Hz Note Juste intonation Gamme de Pythagore Gamme tempérée Mésotonique 1/4 comma Mésotonique 1/6 comma Mésotonique 1/8 comma do 264,00 264,00 264,00 264,00 264,00 264,00 do♯ 275,00 281,92 279,70 275,86 277,86 278,87 ré 297,00 297,00 296,33 295,16 295,77 296,08 mi♭ 316,80 312,89 313,95 309,99 310,95 311,43 mi 330,00 334,13 332,62 330,00 331,37 332,06 fa 352,00 352,00 352,40 350,91 351,27 351,45 fa♯ 371,25 375,89 373,35 368,95 371,25 372,40 sol 396,00 396,00 395,55 394,77 395,18 395,39 sol♯ 412,50 422,88 419,07 412,50 415,93 417,66 la 440,00 445,50 443,99 441,37 442,74 443,43 si♭ 475,20 469,33 470,39 466,43 467,39 467,88 si 495,00 501,19 498,37 493,47 496,03 497,31 do 528,00 528,00 528,00 528,00 528,00 528,00 Dans ce tableau :
- La note DO commune à 264 Hz donne LA à 440 Hz (diapason actuel) dans la juste intonation
- Les gammes naturelles sont représentées par la « juste intonation » à partir de DO
- La gamme de Pythagore est montée de telle façon que la quinte du loup soit entre SOL # et RÉ #
- Les 3 colonnes de droite correspondent aux tempéraments mésotoniques les plus utilisés
Intervalles importants dans 6 systèmes Note Juste intonation Gamme de Pythagore Gamme tempérée Mésotonique 1/4 comma Mésotonique 1/6 comma Mésotonique 1/8 comma Quinte DO-SOL 1,500 1,500 1,498 1,495 1,497 1,498 Quinte du loup SOL 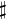 -Ré
-Ré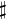
1,536 1,480 1,498 1,531 1,514 1,505 Tierce DO-MI 1,250 1,266 1,260 1,250 1,255 1,258 Dans ce tableau, les intervalles sont calculés à partir du tableau précédent :
- Le tempérament à 1/4 de comma donne des tierces justes et des quintes (y compris le loup) très légèrement fausses ; c'est le plus facile à accorder.
- Le tempérament à 1/6 de comma présente le meilleur compromis, avec des quintes presque toutes équivalentes, des tierces et des quintes proches des intervalles justes
- Le tempérament à 1/8 de comma se rapproche beaucoup du tempérament égal.
Histoire
C’est le théoricien Pietro Aaron qui aurait imaginé, en 1523 à Venise, le tempérament dit « mésotonique ». Les tempéraments mésotoniques ont été utilisés à la fin de la Renaissance et pendant toute la période baroque.
De nos jours ils restent utilisés dans l’accord des instruments à clavier – principalement orgue et clavecin - destinés à l’interprétation de la musique « ancienne » - dans la pratique la musique écrite jusqu’à la moitié du XVIIIe siècle et ceci concurremment avec les tempéraments inégaux qui leur sont postérieurs.
Voir aussi
Articles connexes
- Portail de la musique classique
Catégorie : Justesse
Wikimedia Foundation. 2010.