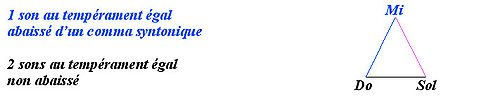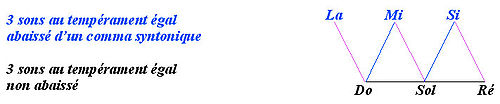Justesse des tierces

La justesse des tierces, étudiée ci-dessous, est un problème pratique qui se pose à tous les musiciens.

Sortir du tempérament égal ?

Dans leur pratique musicale la plus commune, les musiciens utilisent le tempérament égal, fondé sur la division en douze demi-tons égaux de l'intervalle d'octave (toutefois, le piano sort de cette échelle en étant accordé plus haut dans l'aigu : voir Inharmonicité du piano). Cependant, dans un certain nombre de situations, pour d'impératives raisons de justesse, les musiciens sont conduits à sortir de cette échelle, sans en être forcément conscients d'ailleurs. Le cas le plus fréquent où cela se produit est la tenue marquée d'un accord de tierce majeure, particulièrement pour des sons entretenus (chanteurs a cappella, duo de flûte, instruments à vent solistes, formation de jazz avec trombone à coulisse etc.). Les causes du problème résident dans la présence de battements, d'une part, et d'autre part dans le fait que le son résultant (ou son différentiel) qui provient de la conjonction des deux sons de la tierce majeure, s'entend alors très distinctement. Or, dans le tempérament égal, cette troisième note vient fortement perturber la consonance car elle est beaucoup trop haute pour sonner juste (voir ci-dessous). En un tel cas, les musiciens, consciemment ou non, sont conduits à jouer cette tierce majeure petite, plus proche d'une tierce pure (tierce dite "juste") que d'une tierce du tempérament égal. Bien comprendre ces situations peut faire gagner beaucoup de temps, car il existe une recette simple pour savoir gérer ces hauteurs, qui sont étrangères au tempérament égal usuel.

Qu'est-ce qu'un son résultant ?

La notion de son résultant (ou son différentiel) n'est pas forcément familière à tous les musiciens. Il s'agit pourtant d'une propriété générale de l'oreille, de même nature que la perception des battements.

Son différentiel d'un accord de tierce majeure

L'accord de tierce majeure résulte de la conjonction de l'harmonique 4 avec l'harmonique 5 du même fondamental. Par exemple, pour un fondamental do, l'harmonique 4 est le do situé deux octaves au-dessus, l'harmonique 5 est le mi situé au-dessus, à une fréquence 5/4 = 1,25 fois plus grande.

La fréquence du son différentiel est la différence des fréquences de l'harmonique 5 et de l'harmonique 4, c'est-à-dire la fréquence du fondamental 1. Autrement dit, la conjonction du mi, à une fréquence 5/4 = 1,25 fois celle du do, avec ce do, produit un son différentiel à la fréquence 5/4 - 1 = 0,25 fois celle du do, c'est-à-dire 4 fois inférieure, autrement dit un do situé deux octaves plus bas.

Dans le tempérament égal, le mi de l'accord n'est pas à une fréquence 1,25 fois celle du do : il se trouve à 4 demi-tons du tempérament égal, c'est-à-dire à une fréquence 2^4/12 = 1,2599 fois celle du do. L'écart, en rapport de fréquences, est de (2^4/12) / (5/4) = 1,0079 (erreur de l'ordre de 0,8%, soit 13,7 cents sur un accordeur électronique). La fréquence du son différentiel est alors 2^4/12 - 1 = 0,2599 fois celle du do, Par rapport au do situé deux octaves en dessous, la fréquence de cette note est (2^4/12 - 1) / (5/4 -1) = 1,0397 fois trop grande (erreur de l'ordre de 4%, soit 67,4 cents) : il s'agit d'un do trop haut, dont la fausseté se remarque d'autant plus cruellement que l'accord est tenu : un vibrato appuyé ne suffit pas même, alors, à en masquer la défaillance de justesse.

Les quintes du tempérament égal, constituées de 7 demi-tons égaux, sont légèrement plus petites que les quintes pures, constituées des harmoniques 2 et 3 d'un même fondamental. Le rapport de fréquences quinte pure / quinte tempérée est : (3/2) / (2^7/12) = 1,0011 (erreur de l'ordre de 0,1%, soit 2,0 cents). L'erreur est donc très faible : elle n'est pas gênante. Le son différentiel, pour la quinte [do, sol], est le do situé une octave plus bas, avec une erreur (3/2 -1) / (2^7/12-1) = 1,0034. L'erreur (de l'ordre de 0,3%, soit 5,9 cents) est faible également. L'emploi du tempérament égal ne pose donc pas de problème notable de justesse en ce qui concerne les quintes.

L'accord de tierce mineure résulte de la conjonction de l'harmonique 5 avec l'harmonique 6 du même fondamental. Par exemple, pour un fondamental do, l'harmonique 5 est le mi situé deux octaves et une tierce majeure au-dessus, l'harmonique 6 est le sol situé au-dessus de ce mi, à une fréquence 6/5 = 1,20 fois plus grande. Le son différentiel est le fondamental do, situé deux octaves et une tierce majeure en dessous du mi. La tierce mineure étant le complément à la quinte de la tierce majeure, les tierces mineures du tempérament égal sont trop petites chaque fois que les tierces majeures sont trop grandes. Résoudre les problèmes de justesse des tierces majeures résout du même coup celui des tierces mineures.

Rôle pivot du second degré de la gamme majeure

Pour résoudre ce problème de justesse des tierces majeures, instrumentistes à vent et chanteurs abaissent le mi de l'accord de do majeur. Ce mi abaissé peut se représenter graphiquement sur une ligne différente de celle où l'on écrit les quintes du tempérament égal de départ :

Tempérament 2x12 pour 3 sons

Pour le relatif de la mineur, il suffit de prendre le la dans cette série des quintes abaissées, ce qui se représente ainsi :

Tempérament 2x12 pour 4 sons

On complète de façon à pouvoir transposer en sol majeur, ce qui permet également l'utilisation du ton relatif de mi mineur :

Tempérament 2x12 pour 6 sons

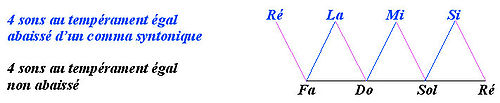
On complète également de façon à pouvoir transposer en fa majeur et ré mineur, ce qui donne :

Tempérament 2x12 pour 8 sons

L'ensemble obtenu montre deux caractéristiques remarquables. La première, c'est que cet ensemble contient la gamme diatonique complète (do, ré, mi, fa, sol, la, si). La seconde, c'est que le second degré de cette gamme, ré, se trouve dédoublé : l'accord mineur [ré, fa, la] utilise le ré bas, celui de la série abaissée, alors que l'accord majeur [sol, si, ré] utilise le ré de la série normale, non abaissée.

La démonstration ci-dessus est due au tromboniste de jazz Raymond Fonsèque^[1], qui avait remarqué que, pour jouer le second degré, il utilisait une position différente de la coulisse de son trombone suivant que l'accord était mineur ou majeur.

Le second degré de la gamme majeure joue donc un rôle très particulier. Il faut modifier sa hauteur selon le contexte, en le jouant bas si l'accord est mineur, mais en le jouant normal si l'accord est majeur. Ce rôle particulier que joue le second degré de la gamme majeure a été remarqué depuis longtemps dans la théorie de l'harmonie.

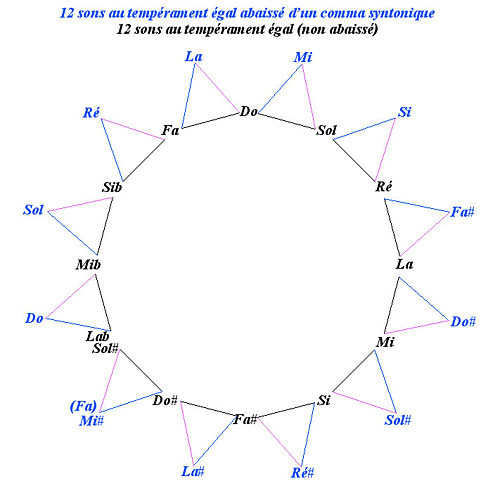
Il apparaît, par exemple, si on écrit les notes de la gamme diatonique complète dans l'ordre des quintes ascendantes fa, do, sol, ré, la, mi, si : les trois premières appartiennent au milieu tonal majeur de do ([fa-la-do], [do-mi-sol], [sol-si-ré], en bleu), les trois dernières au milieu tonal mineur relatif de do ([ré-fa-la], [la-do-mi], [mi-sol-si], en rose), et le ré est la note centrale commune au majeur [sol-si-ré] et au mineur [ré-fa-la], jointure pour le ton de do entre le milieu tonal majeur et le milieu tonal mineur^[2]. Il n'y a que 6 accords parfaits sur les 7 notes car [si, ré, fa] n'est pas un accord parfait (mais il est centré sur ré et contient le triton [si-fa], qui détermine la tonalité à lui seul).

Milieu tonal majeur et milieu tonal mineur d'après Pierre-Yves Asselin. Note pivot, triton.

On qualifie parfois de note pivot le second degré de la gamme majeure^[3].

Système à double tempérament égal

Clavier Fonsèque réalisé par Jean-Paul Rouaud, facteur de clavecins

Partant de do majeur, la démonstration de Raymond Fonsèque permet de comprendre qu'il faut dédoubler le ré, second degré et note pivot de do majeur. Partant de sol majeur, il faut dédoubler la note pivot la. Partant de fa majeur, il faut dédoubler la note pivot sol, etc. Au total, pour douze tons majeurs, il faut dédoubler douze notes pivots, ce qui conduit à utiliser un système de deux fois douze hauteurs du tempérament égal, appelé super-tempérament par Raymond Fonsèque, le second groupe étant abaissé par rapport au premier (d'un coma syntonique).

Tempérament 2x12 pour les 24 sons

La recette pour gérer ces vingt quatre hauteurs est simple : dans le ton où l'on se trouve, on ne change de groupe de douze que pour le second degré de la gamme majeure, cette note étant prise dans le groupe de douze abaissé si l'accord est mineur, mais étant remontée en la prenant dans le groupe de douze normal si l'accord devient majeur.

Cette règle, peut-être peu souvent formulée, semble par contre relativement suivie d'instinct par les musiciens. Pierre-Yves Asselin arrive à cette conclusion après avoir fait une série de tests avec un quatuor vocal a cappella réputé pour sa justesse : après avoir donné une longue série d'enchaînements d'accords à chanter, sans prévenir ces musiciens à l'avance, il a constaté qu'ils suivaient instinctivement cette règle sans faire aucune exception^[4].

On remarque, sur la figure du cercle double des quintes, que les dièses sont abaissés (fa#, do#, sol#, sur le cercle externe) alors que les bémols ne le sont pas (si♭, mi♭, la♭, sur le cercle interne). On retrouve, ici, cette caractéristique connue du tempérament mésotonique à tierces pures et des tempéraments inégaux à tierces quasi-pures dérivés du mésotonique : les bémols sont haut et les dièses sont bas (voir l'article : Inégalités dans la musique baroque).

Cas de l'accord de tierce majeure dominante-sensible

L'accord de septième de dominante, [sol, si, ré, fa] en do majeur, pose un problème particulier en raison de la présence de la note sensible, si pour do majeur. Dans un contexte mélodique, la note sensible subit l'attraction de la tonique, sa voisine un demi-ton plus haut. Il est d'usage, dans un tel contexte mélodique, de jouer la sensible haut. Cependant, dans le cadre d'une cadence où l'accord de septième de dominante [sol, si, ré, fa] amène l'accord de tonique ([sol, do, mi]), cette sensible produit un accord de tierce majeure avec la dominante et la justesse de cet accord impose absolument que la sensible soit jouée bas. En do majeur, la sensible si ne peut-être jouée haut que dans un contexte purement mélodique. Au sein d'une cadence, le si de la tierce [sol, si] doit impérativement être joué bas sous peine de dissonance, particulièrement rédhibitoire dans un contexte où les instruments à vent laissent entendre le son différentiel, deux octaves en dessous du sol.

Notes

Articles en relation

• Gammes et tempéraments
• Gamme tempérée
• Battement
• Son résultant
• Tempérament inégal
• Tempérament mésotonique
• Gamme pythagoricienne
• Gamme naturelle
• Comma
• Tempérament
• Tempérament par division multiple
• Inharmonicité du piano
• Inégalités dans la musique baroque

Liens externes

• http://supertemperament.free.fr

• Portail de la musique
• Portail de la musique classique
• Portail des arts du spectacle
• Portail de la physique
• Portail sur les sciences
• Portail de l’opéra