Intonation Musicale

Pour les articles homonymes, voir Intonation.

L'intonation musicale définit de manière précise la hauteur des notes de musiques jouées ou chantées, les unes par rapport aux autres. On emploie également l'expression justesse d'intonation. On parle d’intonation musicale plus particulièrement dans l'usage pratique quotidien, et de tempérament, de gamme ou système de justesse dans l'usage théorique.

Problématique

Les imperfections des gammes théoriques ne concernent en fait que les instruments dits « à sons fixes » qui, une fois accordés, émettent au cours de la même pièce musicale, toujours la même fréquence pour la même note. Il n'en va pas de même pour la voix humaine ou pour les instruments dits « naturels » (tels le violon et sa famille, certains cuivres) qui peuvent s'adapter en cours d'exécution, à l'environnement modal, pour "ajuster" les intervalles mélodiques ou harmoniques du morceau joué.

Ces instruments permettraient ce que certains appellent la « juste intonation », dans laquelle la plupart des intervalles, qu'ils soient d'octave, de quinte, de tierce etc., simultanés ou successifs seraient purs de telle manière que, selon leur rôle musical, deux notes portant le même nom ne seront pas nécessairement jouées exactement à la même fréquence mais pourront différer de quelques commas.

Lien externe : Essai sur la question de la juste intonation par Olivier Bettens : Utopie ou réalité?

Olivier Bettens :

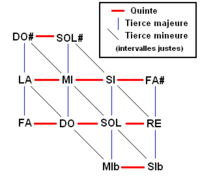
« L'intonation juste a de tout temps été considérée par certains comme une chimère. Ils y voient, peut-être à raison, un caprice de mathématicien sans réel contenu musical. Il n'en demeure pas moins que cette « illusion » a longtemps fait l'objet d'une quête que Haynes n'hésite pas à comparer à celle du Graal. S'il est un point de l'espace-temps où cette quête avait quelque chance d'aboutir, il se situe à coup sûr dans l'une ou l'autre des cappelle et camerate de très haut niveau qui fleurissent dans l'Italie du XVI^e siècle, ce microcosme qui voit « tous les praticiens, mus par l'autorité de Zarlino », rechercher assidûment la meilleure intonation possible. C'est à cette époque plus qu'à n'importe quelle autre que l'intonation juste a pu faire l'objet d'une pratique plus ou moins consciente et raisonnée... Seulement, une telle affirmation gagnerait en consistance si l'intonation juste était autre chose qu'une idée vague. Sa mise en pratique implique en effet des choix qui peuvent conduire à des résultats fort divers. C'est en vain qu'on cherche, dans la littérature ancienne ou moderne, un mode d'emploi permettant de l'appliquer à des exemples musicaux concrets. »

Accord selon la juste intonation

Cette recherche d'intonation est généralement inaccessible aux instruments à sons fixes dits aussi « instruments tempérés » : ce sont les plus nombreux. Il est toutefois possible d'accorder ces instruments avec le maximum de quintes, tierces majeures et tierce mineures justes, comme le montre le schéma, mais évidemment certains intervalles ne peuvent pas l'être.

La théorie mathématique de la musique rend compte de la difficulté d'établissement des gammes et démontre même l'impossibilité de leur perfection, mais ce sont bien des contraintes pratiques et purement musicales qui introduisent la notion de tempérament.

Intonation « naturelle » et intonation tempérée

Qu'est-ce que jouer juste ? Qu'est-ce qui conduit l'artiste à choisir une hauteur plutôt qu'une autre ? Lorsqu'on approfondit la question, on s'aperçoit que les chemins vers une hauteur idéale peuvent êtres forts divers.

Intervalles naturels

Les intervalles dits naturels sont les intervalles de notes qui ont un rapport de fréquence défini par une fraction simple. Depuis l'antiquité on a utilisé l'unisson (1/1), l'octave (2/1), la quinte (3/2), la quarte (4/3) et le ton (9/8), depuis la Renaissance (Zarlino) on mit à l'honneur la tierce majeure pure (5/4) et la sixte correspondante (8/5), la tierce mineure pure (6/5) et la sixte correspondante (5/3).

Ces rapports « simples » (rapports de nombre entiers petits) s'expliquent par la notion de battement. En effet, si des sons ont des fréquences proches, il se créent des variations rapides du volume sonore, utilisées notamment par les musiciens pour s'accorder. Ces battements sont perçus comme désagréables (ils sont utilisés à dessein dans certaines alarmes). Par contre, pour une octave, les fréquences sont doubles et il ne se produit pas de battement. C'est le rapport des fréquence qui détermine l'absence ou la présence de battements.

Note

D'un point de vue mathématiques, on a une échelle exponentielle (qui « transforme » les additions en multiplications) : ajouter une quarte, cela revient à multiplier la fréquence par 4/3 ; retrancher une quarte, cela revient à diviser par 4/3 (c'est-à-dire à multiplier par 3/4).

Composition d'intervalles naturels

On peut construire d'autres intervalles par composition d'intervalles naturels. Par exemple, on peut obtenir un ton par l'addition d'une quinte et la soustraction d'une quarte.

Mathématiquement, cela fait 3/2 × ¾ = 9/8, c'est-à-dire un ton naturel ascendant.

Mais si on répète l'opération, c'est-à-dire si l'on additionne deux tons, on ne trouve pas la tierce majeure naturelle (dite « pure ») mais la tierce pythagoricienne: (9/8) × (9/8) = 1,265625 et non 5/4. Et les demi-tons obtenus par différence avec la quarte ne valent ni l'un ni l'autre la moitié du ton naturel.

Les différents systèmes

Rien n'est parfait et il faut choisir l'outil avec lequel on veut travailler : Le système de Pythagore, dont les notes sont définies par quintes pures à partir d'un ton de base fait entendre des quintes et des octaves parfaites, mais des tierces très médiocres. Le système de Zarlino dont les notes sont définies par la qualité de leur consonance par rapport au ton de base fait entendre certaines tierces pures magnifiques, mais d'autres ne le sont pas.

Deux possibilités se présentent ensuite :

• Si l'on joue sur un instrument à intonation fixe, on tempère l'accord, c'est-à-dire qu'on fait des compromis.
• Si l'on joue sur un instrument à intonation libre, on a la possibilité d'adopter une intonation changeante, ce qui est un autre compromis.

Voir à ce sujet un dossier extrêmement élaboré sur la justesse a cappella à la Renaissance:

http://virga.org/zarlino/

L'accord à tempérament égal a pu s'imposer petit à petit au XIX^e siècle grâce à ce que :

• La musique d'ensemble ne laisse généralement pas entendre de façon nette les consonances parfaites, et l'emploi du vibrato renforce cette tendance.
• La musique a exploité à fond la modulation, et n'a plus voulu sacrifier certaines tonalités au profit d'autres. La gamme par tons et la musique atonale réclament absolument le tempérament égal.
• Le mélodisme et la virtuosité ont continuellement gagné en importance, rendant l'exigence en matière de consonance moins grande que pour les polyphonies de la renaissance.
• L'intonation changeante est plus difficile.
• Le piano, accordé en tempérament égal par nature, a été omniprésent dans la vie musicale.

Voici quelques rapports de fréquence à partir de do qui donnent une idée des grandeurs : (Le « cent » est une valeur physique correspondant à 1/100^e de ½ ton tempéré.)

Intervalles naturels	Différence	Intervalles tempérés	Différence	Intervalles Pythagoriciens
		Do	1,000000		
		Doréb	1,059463		
(Ré-mi 10/9)
Ré 9/8 = 1,125	(<12,3 cents<)
> 3,9 cents >	
Ré	1,122462	
< 3,9 cents <	
naturel
Mib 6/5 = 1,2	> 15,6 cents >	Rémib	1,189207	> 5,9 cents >	Mib 32/27 = 1,185185
Mi 5/4 = 1,25	< 13,7 cents <	Mi	1,259920	< 7,8 cents <	Mi 81/64 = 1,265625
Fa 4/3 = 1,333333	< 2 cents <	Fa	1,334839	> 2cents >	naturel
		Fasolb	1,414213		
Sol 3/2 = 1,5	> 2 cents >	Sol	1,498306	< 2 cents <	naturel
Lab 8/5 = 1,6	> 13,7 cents >	sollab	1,587401		
La 5/3 = 1,666666	< 15,6 cents <	La	1,681792	< 5,9 cents <	La 27/16 =1,6875
		Lasib	1,781797		
		Si	1,887748	< 9,8 cents <	Si 243/128=1,898437

On le voit, les intervalles les plus problématiques sont les tierces et les sixtes. La différence entre le mi naturel et le mi pythagoricien est de 21,5 cents. On peut la réaliser sur un violon accordé en quintes justes : le mi de la corde ré peut se définir par quarte pure à partir du la à vide, et se définir par sixte pure à partir du sol à vide. Le deuxième est beaucoup plus bas à 3,7 mm de distance sur la touche. (Ils définissent avec le ré à vide respectivement un ton naturel majeur et un ton naturel mineur)

Justesse

Lequel des deux est juste ?

Sur le plan harmonique, on peut préférer le mi « naturel » (c. à d. formant une tierce naturelle avec le do dans le cadre de notre exemple), mais sur le plan technique il sera plus commode de faire le mi tempéré, et sur le plan mélodique, on pourra préférer le mi pythagoricien à cause de l'attraction mélodique descendante fa-mi. La tierce naturelle est un tabou pour l'école franco-belge de violon, est refusée par les grecs anciens, mais est au contraire très prisée par la renaissance au point de sacrifier les quintes. Les tenants de la tierce naturelle trouveront que la tierce tempérée est insupportable, et vice versa…

Par ailleurs, les instrumentistes à vents sont indécis entre les tierces tempérées données par l'accordeur électronique et les tierces naturelles données par la consonance avec leurs collègues. Les instrumentistes à cordes sont indécis entre les tierces tempérées données par l'égalité nécessaire de leurs intervalles (surtout dans les gammes chromatiques ; ils utilisent rarement l'accordeur électronique qui est instable au son des instruments à cordes), et les tierces pythagoriciennes données par l'enchaînement des quintes. Quant aux choristes, ils ont souvent tendance à monter avec des tons mineurs et des tierces naturelles, puis à descendre avec des tons majeurs et des tierces pythagoriciennes, ce qui est fâcheux...

Musiques extra-européennes

De nombreux systèmes d'intonation ne sont pas tempérés et exigent aussi une grande précision, souvent inférieure à 10 cents, tout en ne reposant pas forcement integralement, sur des lois dites « naturelles » de la résonance : Par exemple, les musiciens Are-Are, qui accordent leurs flûtes de pan en échelles équiheptatoniques (Hugo Zemp, CNRS, disque collection Musée de l'Homme, Paris). De même, par exemple, comme le montrent les travaux de Simha Arom et de son équipe entre 1986 - 1994 au sujet des systèmes d'intonation des pygmees Aka. Et bien d'autres ethnomusicologues et traditions orales (Indonésie, Amériques...).

Articles connexes

• Introduction à la justesse en musique
• Tempérament
• Comma
• Gammes et tempéraments
  • Gamme pythagoricienne
  • Gamme naturelle
  • Gamme tempérée ou Tempérament égal
  • Tempérament mésotonique
  • Tempérament inégal
  • Tempérament par division multiple

Annexe

Le « Tempérament égal à quintes justes », un système d'intonation du XXe siècle pour l'orchestre et le piano. (Extrait du livre de Serge Cordier : « Piano bien tempéré et justesse orchestrale » , éd. Buchet-Chastel, 1982), et commentaires

Bibliographie

• Dominique Devie: le tempérament musical
• Pierre-Yves Asselin: musique et tempérament
• Jean Lattard: gammes et tempéraments musicaux
• Eric Emery: la gamme et le langage musical
• Alain Daniélou: traité de musicologie comparée
• S. Cordier: piano et justesse orchestrale ed. Buchet-Chastel 1982

Liens externes

• approche pédagogique sur la justesse

• Portail de la musique