Symbolique des figures géométriques

La symbolique des figures géométriques est l'étude des figures géométriques (point, lignes, surfaces, volumes) en tant que symboles, dans leur capacité à désigner, à signifier ou même à agir.

Le symbolisme des figures géométriques concerne les dimensions en tant que symboles, dans leur puissance à représenter analogiquement, à être interprétés, à porter sens et valeurs (en plus de l'aspect pratique ou scientifique). On entre dans l'étude des figures géométriques en tant que symboles (symbologie) ou en tant que systèmes (symbolique) ou dans l'examen de leur capacité à désigner, à signifier, voire à exercer une influence (symbolisme). La figure géométrique en général a son symbolisme (elle représente les limites, l'étendue des choses), et chaque figure géométrique en particulier a son symbolisme (la sphère représente le milieu parfait, le cercle représente l'espace clos).

Galilée (qui ne croyait pas au symbolisme, à la différence de Kepler) : "La philosophie est écrite dans ce vaste livre constamment ouvert devant nos yeux (je veux dire l'univers), et on ne peut le comprendre si d'abord on n'apprend à connaître la langue et les caractères dans lesquels il est écrit. Or il est écrit en langue mathématique, et ses caractères son le triangle et le cercle et autres figures géométriques, sans lesquelles il est humainement impossible d'en comprendre un mot" (L'Essayeur. Il Saggiatore, 1623 ; in Dialogues et lettres choisies de Galilée, Hermann, 1966).

Sommaire 1 Distinctions 2 Le système des figures géométriques en tant que symboles 3 Analogies et correspondances 4 Techniques de décodage 5 Quelques figures géométriques 6 Histoire 7 Les panneaux routiers (code de la route) 8 Les émoticônes 9 Inde : mandala et yantra 10 Bibliographie 11 Voir aussi 11.1 Articles connexes 11.2 Liens externes 12 Notes et références

Distinctions

• Figures géométriques et formes. La notion de figure (en géométrie) est plus étroite que celle de forme (morphologie) : elle regroupe points, lignes, surfaces, volumes, alors que la notion de forme est très large : il y a les formes statiques (carré, triangle, croix, étoile, x, etc.), les formes dynamiques (spirale, polyèdre, courbe), les formes ni statiques ni dynamiques (la ramification). Selon le Bauhaus, les formes primitives sont le rectangle, le cercle, le triangle ; les formes dérivées : le pentagone, le demi-cercle + le démi-hexagone, le demi-carré + le demi-hexagone.
• Figures : points, lignes, surfaces, volumes. 1) Points. 2) Lignes : lignes soit continues soit discontinues ; lignes soit droites (carré, rectangle, triangle, losange... ; croix, chevrons, svastika, flèche, escalier...) soit courbes (cercle, ellipse, ovale, onde, spirale, sinuosité, boucle, ondulation, serpentin, concavité, convexité...) soit ni droites ni courbes (l'hélice) ; lignes soit parallèles soit perpendiculaires. 3) Surfaces (figures géométriques à deux dimensions de l'espace) : cercle, triangle, carré, rectangle, losange, trapèze, ellipse, pentagone, hexagone, octogone, décagone, dodécagone... 4) Volumes (figures géométriques à trois dimensions, limitées par des surfaces) : cube, parallélépipède, tétraèdre, sphère, tas de sable, prisme droit, tore, pyramide, cône, cylindre... ; les polyèdres réguliers : tétraèdre, cube, octaèdre, dodécaèdre, icosaèdre.
• Symbolisme des figures géométriques et symbolique des figures géométriques. 1) Par symbolisme des figures géométriques, on entend la capacité qu'a un figure de désigner autre chose que elle-même. Par exemple, le cercle véhicule le symbolisme de la perfection. Le symbolisme des figures concerne donc leur capacité à représenter : non seulement à signifier des êtres ou des pensées, peut-être à agir, influencer, activer les esprits ou les choses, mais encore à être interprétés. Le symbolisme est donc la puissance d'une chose à désigner, signifier, révéler. 2) Une symbolique est un ensemble, un système de symboles. La symbolique des figures concerne le système signifiant des figures : d'une part, elles forment ensemble un système, un tout, un ensemble, un complexe, d'autre part, chacune entre dans un réseau de symboles, forme une constellation avec d'autres symboles (chacune appelle son opposé, son proche, etc.). 3) La symbologie est la théorie des symboles.
• Sémiotique : syntaxe, sémantique, pragmatique. L'approche sémiotique, depuis Charles W. Morris^[1], examine trois points de vue : 1) la syntaxe (les rapports entre figures), 2) la sémantique (le sens des figures, ce qu'elles désignent indirectement, par analogie naturelle), 3) la pragmatique (l'utilisation des figures symboliques dans une situation de communication).

Le système des figures géométriques en tant que symboles

Une symbolique implique un système, c'est-à-dire une complexité variée (elle comporte plusieurs éléments), interactive (ses éléments agissent les uns sur les autres), organisée (elle obéit à un ordre, tel que succession, priorité), totale (quand on modifie un élément les autres sont modifiés) et finalisée (elle vise un but, en général la signification). Il faut donc voir le système des figures quand on les examine, même individuellement, en tant que symboles.

Analogies et correspondances

• Voir : Analogies et correspondances.

Figures géométriques et couleurs. Kandinsky, au Bauhaus, établit une corrélation entre les trois formes géométriques élémentaires et les trois couleurs primaires : triangle jaune, carré rouge, cercle bleu.

Figures géométriques et lettres. Déjà, Geofroy Tory (Champ fleuri de la vraie proportion des lettres antiques, 1500), suppose que les lettres, inventées par inspiration divine, ont été constituées à partir de droites et de cercles.^[2] L'école du Bauhaus a mis au point une typographie "universelle" qui réduit l'alphabet romain en formes géométriques simples.

Figures géométriques et nombres. Depuis le pythagoricien Philolaos et Platon, "le 1 est le point, le 2 la ligne, le 3 le triangle [le plan], le 4 la pyramide [le volume]."^[3] - Figures géométriques et chiffres : le chiffre zéro (O) a la forme de la lettre 0, le chiffre 1 celle de la lettre l, etc.

Figures géométriques et pierres. Le système cristallin de la chrysolithe, de la fluorite, du grenat, de la pyrite, de la chrysolithe est cubique ; celui de l'aigue-marine, du béryl, du critsal, de l’émeraude, de l'opale, de la sélénite (pierre de lune) est hexagonal.[1] Le diamant est cubique ou hexagonal.

Techniques de décodage

Il y a deux niveaux dans l'art de décoder (identifier et interpréter) les symboles, leur code : le déchiffrage et le décryptage. Quand on déchiffre, on connaît le code ; quand on décrypte : on ne le connaît pas.

• Première technique : le symbolisme des formes. "Regardez les formes. Elles sont composées de droites et de courbes. Dans la symbolique traditionnelle, la droite est reliée à la polarité masculine et la courbe à la polarité féminine. Cette particularité "sexuelle" n'est pas fortuite pour celui qui sait que tout s'accouple selon des lois, des codes qui font du hasard un leurre. La complémentarité des polarités permet une "auto-fécondation".

La droite horizontale. Elle représente notre plan terrestre, "plat" par son horizon et sa stabilité apparente. C'est une structure d'accueil de notre matière dont elle est le symbole. Elle est aussi le symbole masculin.

La droite verticale. Elle représente l'Esprit Divin. Elle est une descente de ce "qui est en haut" en reliant le supérieur et l'inférieur. Ce qui est debout, à l'image de l'humain, est ce qui est doué d'esprit, d'intelligence, étant le lien entre le monde divin et les mondes inférieurs. Regardez la symbolique de l'arbre, ce pilier vertical qui est dans les traditions le lien entre le ciel et la terre et vénéré comme tel.

La diagonale. Elle désigne un mouvement, qui est une progression ou une ascension selon le sens du tracé. Ce mouvement peut être un mouvement temporel ou une capacité d'action, de faire.

La demi-sphère : matrice. Elle est le symbole de la féminité en attente de fécondation.

Le demi-carré. Il symbolise l'homme dans sa polarité incomplète. Ce carré que l'on devine, c'est son coté cartésien, "carré", et pourtant tronqué de moitié car il lui manque son autre moitié.

Le cercle : Il représente un tout fini, complet et parfait, autonome, et pourtant cerné par sa propre limite. Il contient son propre espace, c'est un contenant et un contenu." [2]

• Deuxième technique : identifier les objets portant telle figure. D'une part, qu'est-ce qui est circulaire, triangulaire... ? D'autre part quel est le ou les points communs entre les objets circulaires, ou triangulaires... ?
• Troisième technique : examiner les rapports avec les autres figures. A quelle figure la triangularité de tel objet est-elle opposée, ou accouplée, ou similaire ?
• Quatrième technique : quel effet produit psychologiquement telle figure ? Le cercle apaise.
• Cinquième technique : que disent les traditions (proverbes, mythes, contes, etc.) et les idéologues (philosophes, théologiens, iconographes, etc.) ?

Quelques figures géométriques

Il est tentant de vouloir traduire, allégoriquement, une figure géométrique en termes de qualité, de signification, comme fait, par exemple, le site "Ligne et formation". Bien entendu, l'exercice est risqué, peut-être même sans signification, parce que les symboles ont plusieurs sens (parfois même contraires), parce que les symboles changent de sens selon les cultures, parce que le sens d'un symbole n'est jamais indépendant des symboles qui l'entourent (le carré comme symbole change de sens selon qu'il est confronté au cercle ou au rectangle).

• Carré : l'absence rassurante de tension.
• Cercle : la perfection, l'absolu, l'infini.
• Losange : la vie, le passage, l'échange.
• Rectangle s'apparente au carré. (Présenté à la française, c'est-à-dire à la verticale, il est plus dynamique ; à l'italienne, c'est-à-dire à l'horizontale, il produit un effet panoramique.)
• Triangle : l'harmonie, la proportion, la sécurité.

Histoire

Le plus grand et le premier représentant de la symbolique des figures géométriques en Occident, c'est Pythagore et les pythagoriciens. Ils considèrent le cercle et la sphère comme des figures parfaites. Ils recommandent le "triangle pythagoricien", fait de côtés 3, 4 et 5^[4], avec un 3 mâle, un 4 femelle et un 5 symbole du mariage entre mâle et femelle. Sur la base de l'analogie entre nombres et figures, donc entre arithmétique et géométrie, le pythagorisme établit des correspondances entre un et point, deux et ligne, trois et triangle, quatre et carré. Pour le pseudo-Jamblique, "1 est le point, 2 la ligne, 3 le triangle, 4 la pyramide [tétraèdre]" (Théologoumènes arithmétiques, IV° s.).

Platon, dans le Timée, pense que les quatre Éléments sont faits de particules cubiques (pour la Terre) (Timée, 55d), icosaédriques (pour l'Eau), octaédriques (pour l'Air), tétraédriques (pour le Feu) (Timée, 56), et la sphère du monde (le Tout) est un dodécaèdre. Les Éléments sont donc liés aux surfaces des polyèdres réguliers (les solides de Platon) alors connus : tétraèdre (pyramide) (Timée, 56b), hexaèdre régulier (cube), octaèdre, icosaèdre ; le Tout est un dodécaèdre (Timée, 55c). Le Feu, l'Air et l'Eau sont faits de triangles équilatéraux (24, 48, 129 triangles élémentaires scalènes), la Terre de carrés (24 triangles élémentaires isocèles), le Tout de pentagones (12 pentagones irréductibles aux triangles). Dans son enseignement oral ésotérique, Platon établit des correspondances entre dimensions (unité ou nombres ou lignes insécables, lignes ou longueurs, surfaces ou plans, volumes ou solides), figures (lignes insécables, lignes, triangle, pyramide) et nombres (1, 2, 3, 4 : les nombres de la Décade), mais aussi Éléments.^[5] Ainsi, derrière l'analogie entre dimensions, figures, nombres, Éléments, s'établissent les correspondances entre unité/lignes insécables/un/Feu, entre longueurs/lignes/deux/Air, etc. "Ce qui est absolument indivisible, mais avec position, est un point ; ce qui est divisible selon une dimension est une ligne ; ce qui est divisible selon deux dimensions est une surface ; ce qui est absolument divisible en quantité et selon trois dimensions est un corps [un volume]" (Aristote, Métaphysique, Delta, 6, 1016 b).

Les cinq polyèdres réguliers convexes (solides de Platon)
Tétraèdre	Hexaèdre ou Cube	Octaèdre	Dodécaèdre	Icosaèdre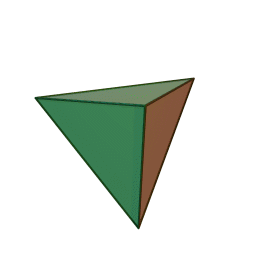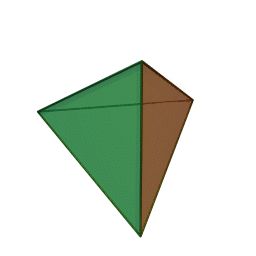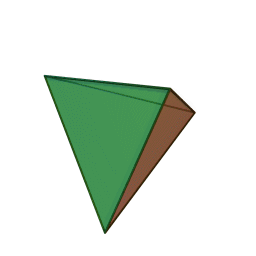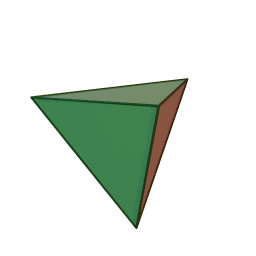

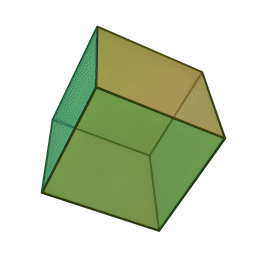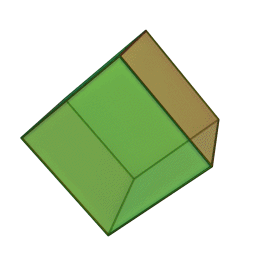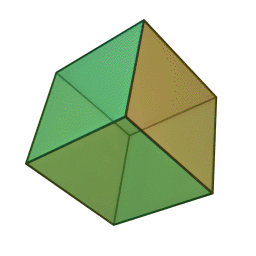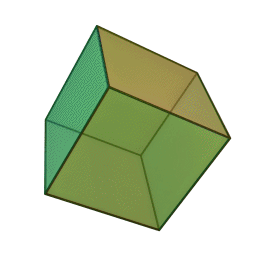
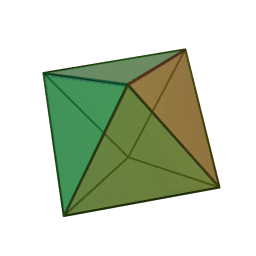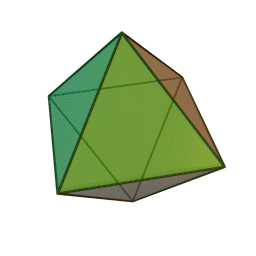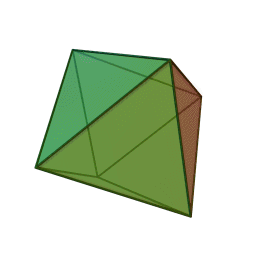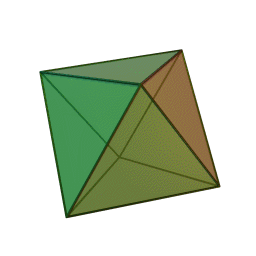
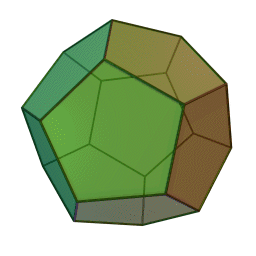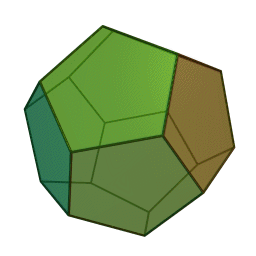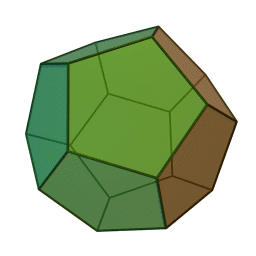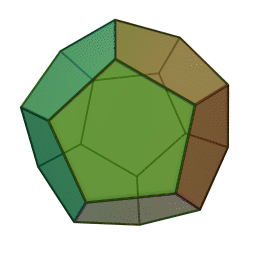
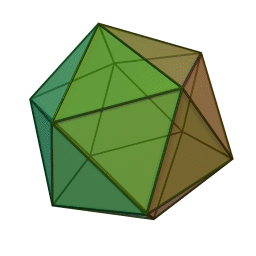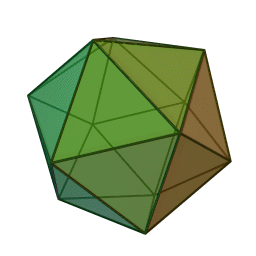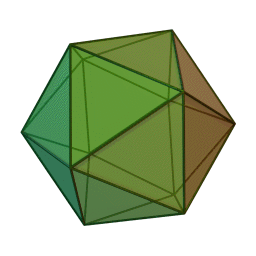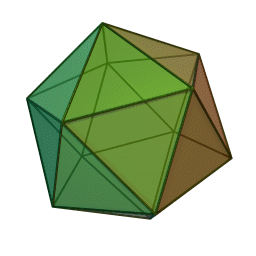
Les platoniciens de l'ancienne Académie (Speusippe, Xénocrate) ont systématisé les correspondances entre les quatre figures géométriques (points, lignes, surfaces, volumes) et les quatre modes de connaissance (intellect, science, opinion, sensation). Aristote : "Platon [dans son enseignement oral ésotérique] s'exprime autrement : l'intellect est l'un [le point, aussi], la science est le deux car elle s'avance d'une direction unique vers un seul point [la ligne], le nombre de la surface est l'opinion, et celui du volume est la sensation" (De l'âme, I, 2). Plutarque met en relation les cinq solides selon Platon dans le Timée et les cinq "grands genres" selon Platon dans le Sophiste : le cube symbolise l'Élément Terre et la catégorie repos, la pyramide symbolise le Feu et le mouvement, l'icosaèdre l'Eau et la différence (l'autre), l'octaèdre l'Air et l'identité (le même), enfin le dodécaèdre figure l'être.^[6]

Pour Macrobe, le plan fondamental est le rectangle et le volume fondamental le parallélépipède (Commentaire du 'Songe de Scipion').

Raymond Lulle, dès 1274, représente son système philosophique grâce à une combinatoire utilisant trois figures : le triangle (symbole de Dieu, de la Trinité), le cercle (symbole du ciel, avec ses planètes et signes zodiacaux), le carré (symbole de la Terre, avec ses quatre Éléments).

John Dee a écrit un ouvrage décisif, La monade hiéroglyphique (1564). Excellent mathématicien et magicien audacieux, il montre graphiquement comment construire les hiéroglyphes des planètes ou des métaux avec des figures élémentaires : le point, la droite, le croissant (la Lune), le cercle (le Soleil), la croix (les quatre Éléments), deux demi-cercles. Il opère par rotations, déstructurations, combinaisons et permutations. Par exemple, le hiéroglyphe de Mercure est fait d'un croissant (tourné vers le haut), d'un cercle, d'une croix. 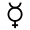[3]

Copernic, en 1605, découvre que chaque planète décrit, non pas un cercle, mais une ellipse dont le Soleil est un foyer. Le monde céleste n'obéit donc pas à l'idée que le cercle soit la figure parfaite.^[7]

Ernst Chladni, vers 1807, prit un disque de cuivre saupoudré de sable et en frotta le bord avec un archet : il obtint des figures géométriques. "Qu'on juge de mon étonnement en voyant ce que personne n'avait encore vu. Il apparut une étoile à 10 ou 12 rayons, qui m'évoqua aussitôt les expériences sur les figures électriques [de Lichtenberg, en 1777]." Ce sont les figures acoustiques de Chladni.

Le Bauhaus, en particulier Johannes Itten entre 1919 et 1923, a développé une symbolique des formes, des couleurs.

En 1917 puis 1942, D'Arcy Thompson publie Forme et croissance (Growth and Form).^[8]. Il montre comment la nature passe d'une forme à une autre.

Selon Robert Ambelain, spécialiste de magie cérémoniale, les formes les plus simples sont le cercle, le triangle, le carré, en volume la sphère, la pyramide, le cube ; symboliquement et rituellement, "le cercle enferme, le carré émet".

Les panneaux routiers (code de la route)

La forme (triangle, ou rond, ou carré, rectangle) et la couleur (blanc, noir ; rouge, jaune, bleu) des panneaux définissent leur fonction :

• Triangle
  • Rouge : danger
  • Rouge et jaune : danger temporaire
• Rond
  • Rouge : interdiction
  • Bleu : obligation
• Carré/rectangle : indication/direction

Les émoticônes

Une émoticône est une courte représentation d'une émotion, d'un état d'esprit ou d'une ambiance, utilisée dans un discours écrit. La tendance est née de la combinaison de certains caractères ASCII, mais le terme peut aussi désigner une petite image ou une forme là où c'est possible. Elle permet de restituer brièvement, à l'écrit, une information comparable à une expression faciale, au ton de la voix ou à une gestuelle à l'oral.

Inde : mandala et yantra

• Voir : mandala.
• Voir : yantra.

Bibliographie

• John Dee, Monas hieroglyphica (1564), trad. par Gillot de Givry (1925) : La monade hiéroglyphique [4]
• René Guénon, Le symbolisme de la croix (1931)
• Jean Chevalier et Alain Gheerbrant, Dictionnaire des symboles (1969), Robert Laffont, coll. "Bouquins"
• Omraam Mikhaël Aïvanhov, Le langage des figures géométriques, Prosveta, 1984..
• R. Begey, La géométrie sacrée ou la magie des formes, Le Rocher, 1995.

Voir aussi

Articles connexes

• Analogies et correspondances
• Ésotérisme
• Géométrie
• Occultisme
• Pentagramme | Sceau de Salomon
• Signe (homonymes) | signe |(sémiologie) | Symbole
• Solide de Platon
• Symbolique
• Symbolisme des chiffres | Symbolisme des lettres | Symbolisme des nombres| Symbolisme des couleurs
• Symbologie

Liens externes

• [5] symbolisme des formes géométriques
• [6] symbolique du carré
• [7] symbolique du cercle
• [8] symbolique du triangle
• [9] symbolique des lignes et des formes
• [10] symbolisme des figures dans l'architecture romane

Notes et références