- Suites adjacentes
-
Théorème des suites adjacentes
En mathématiques, le théorème des suites adjacentes concerne les suites réelles et précise que deux suites adjacentes convergent vers la même limite.
Définition
Deux suites réelles (an) et (bn) sont dites adjacentes si l'une des suites est croissante (au sens large), l'autre suite décroissante au sens large et si la différence des deux tend vers 0.
On supposera par la suite que (an) est croissante et (bn) est décroissante.
On trouve souvent la condition supplémentaire : pour tout entier n,
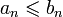 . Cette condition permet de mieux visualiser ce que représentent deux suites adjacentes, elle n'est cependant qu'une conséquence des deux autres conditions. En effet, si (an) est croissante et (bn) décroissante alors (bn − an) est décroissante. Si la suite (bn − an) est décroissante et converge vers 0 alors (bn − an) est une suite à termes positifs. Donc, pour tout n,
. Cette condition permet de mieux visualiser ce que représentent deux suites adjacentes, elle n'est cependant qu'une conséquence des deux autres conditions. En effet, si (an) est croissante et (bn) décroissante alors (bn − an) est décroissante. Si la suite (bn − an) est décroissante et converge vers 0 alors (bn − an) est une suite à termes positifs. Donc, pour tout n, 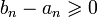 donc
donc 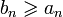 .
.Énoncé
Théorème des suites adjacentes — Soient (an) et (bn) deux suites adjacentes (où (an) est croissante et (bn) est décroissante). Alors ces deux suites sont convergentes, et ont la même limite
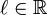 . De plus, pour tout entier naturel n,
. De plus, pour tout entier naturel n, 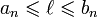 .
.Ce théorème est une conséquence de la propriété de la borne supérieure: tout ensemble de réels non vide et majoré possède une borne supérieure. Ce théorème n'est donc pas valable si on travaille dans l'ensemble des rationnels et que l'on cherche une limite rationnelle.
On démontre même que cette propriété est équivalente à celle de la borne supérieure. Elle offre l'avantage, par rapport à la propriété des suites croissantes majorées, de faire plus que prouver la convergence d'une suite. Elle en donne un encadrement aussi fin qu'on le souhaite.
DémonstrationSi tout ensemble non vide majoré possède une borne supérieure alors deux suites adjacentes convergent vers la même limite
- Si tout ensemble non vide majoré possède une borne supérieure, alors tout ensemble non vide minorée possède une borne inférieure. En effet, si E est un ensemble non vide minoré alors - E est un ensemble non vide majoré. Il possède une borne supérieure B. Alors -B est la borne inférieure de - E.
- L'ensemble
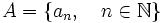 est un ensemble non vide majoré par b0. Il possède donc une borne supérieure Ma. Cette borne supérieure est la limite de la suite (an). En effet, pour tout
est un ensemble non vide majoré par b0. Il possède donc une borne supérieure Ma. Cette borne supérieure est la limite de la suite (an). En effet, pour tout  positif,
positif, 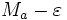 n'est pas un majorant de A. Donc il existe un entier N, tel que
n'est pas un majorant de A. Donc il existe un entier N, tel que 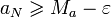 . Comme la suite est croissante, pour tout
. Comme la suite est croissante, pour tout 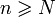 , on aura
, on aura 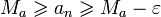 . Ce qui prouve que la suite (an) converge vers Ma.
. Ce qui prouve que la suite (an) converge vers Ma. - On démontre de même que la suite (bn) converge vers un réel Mb
- Puisque la suite (bn − an) converge vers 0, on aura Ma = Mb. Les suites convergent donc vers la même limite
Si toutes suites adjacentes convergent vers la même limite alors tout ensemble non vide majoré possède une borne supérieure.
- Soit E un ensemble contenant un élément x et majoré par M.
- Si x est un majorant de E alors x est la borne supérieure de E.
- Sinon, on procède par dichotomie pour prouver que
 possède une borne supérieure (plus petit des majorants). On crée deux suites
possède une borne supérieure (plus petit des majorants). On crée deux suites 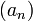 et
et 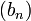 définies par récurrence de la manière suivante :
définies par récurrence de la manière suivante :
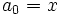 et
et 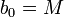
- pour tout entier
 ,
,
- si
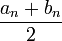 est un majorant ,
est un majorant , 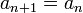 et
et 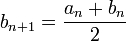
- si
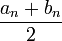 n'est pas un majorant ,
n'est pas un majorant , 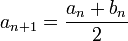 et
et 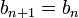
- si
- Le principe de construction assure que
- la suite (an) est une suite croissante dont aucun terme n'est majorant de E
- la suite (bn) est une suite décroissante dont tous les termes sont majorants de E
- pour tout entier n,
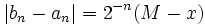 , donc la suite (bn − an) converge vers 0.
, donc la suite (bn − an) converge vers 0.
- Les suites sont donc adjacentes et convergent vers la même limite
 .
.
- Il reste à montrer que
 est bien la borne supérieure.
est bien la borne supérieure. - Pour tout réel
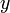 de
de  ,
, 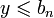 car
car 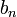 est un majorant. Donc par passage à la limite, pour tout réel
est un majorant. Donc par passage à la limite, pour tout réel 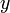 de
de  ,
, 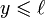 .
.  est donc bien un majorant de
est donc bien un majorant de  .
. - Pour tout réel
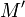 majorant de
majorant de  ,
, 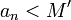 car
car 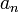 n'est jamais un majorant. Par passage à la limite, pour tout majorant
n'est jamais un majorant. Par passage à la limite, pour tout majorant 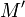 de
de  ,
, 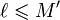 .
.  est bien le plus petit des majorants.
est bien le plus petit des majorants.
Pour tout n,
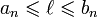
- C'est une simple conséquence de la construction de la limite
 . C'est la borne supérieure de l'ensemble
. C'est la borne supérieure de l'ensemble 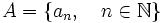 donc, pour tout entier n,
donc, pour tout entier n, 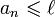 . C'est la borne inférieure de l'ensemble
. C'est la borne inférieure de l'ensemble 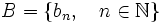 donc, pour tout entier n,
donc, pour tout entier n, 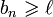 .
.
Utilisation
On rencontre le théorème des suites adjacentes dans tous les problèmes utilisant la méthode de la dichotomie, dans le développement décimal d'un réel, dans l'écriture en fraction continue ainsi que dans de nombreux problèmes de quadrature (quadrature du cercle, de la parabole).
On retrouve une variante des suites adjacentes dans le critère de Leibniz sur les séries alternées : si (un) est une suite à termes positifs décroissante et convergeant vers 0, la série
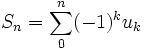 converge.
converge.- En effet, les suites (an) et (bn) définies par bn = S2n et an = S2n + 1 sont des suites adjacentes qui convergent donc vers la même limite
 .
.
- Portail des mathématiques
Catégories : Suite | Théorème de mathématiques
Wikimedia Foundation. 2010.
