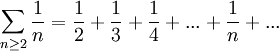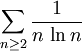Série de bertrand

Série de Bertrand

Pour $α$ et $β$ deux réels, on appelle série de Bertrand la série à termes réels positifs suivante :

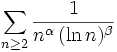$\sum_{n\ge 2}{1 \over n^\alpha\,(\ln n)^\beta}$ .

La série harmonique en est un cas particulier (au premier terme près), pour $α = 1$ et $β = 0$ :

$\sum_{n\ge 2}{1 \over n} = \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{n}+...$

Théorème de Bertrand — Une série de Bertrand converge si et seulement si α > 1 ou (α = 1 et β > 1).

Cette condition nécessaire et suffisante est parfois résumée en : « le couple $(α,β)$ est lexicographiquement postérieur à $(1,1)$ ». Cela se réfère à l'ordre lexicographique, adopté pour trier les mots dans un dictionnaire : on tient compte de la première lettre, puis de la deuxième, etc.

Exemple :

On sait que la série harmonique diverge, et que la série 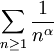$\sum_{n\ge 1}{1 \over n^\alpha}$ converge si et seulement si $α > 1$ (série de Riemann). Bien sûr, si $α > 1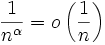$ , ${1 \over n^\alpha}=o\left(\frac{1}{n}\right)$ , cependant il existe des séries dont le terme général est négligeable devant $\frac{1}{n}$ mais qui divergent.

La série de Bertrand permet alors d'exhiber un contre-exemple à l'implication erronée suivante : 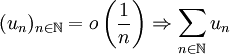$(u_n)_{n\in\N}=o\left(\frac{1}{n}\right)\Rightarrow \sum_{n\in\N} u_n$ converge. La « (1,1)-série de Bertrand », ie la série :

$\sum_{n\ge 2}{1 \over n\,\ln n}$

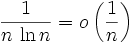est divergente, d'après la proposition, alors que ${1 \over n\,\ln n}=o\left(\frac{1}{n}\right)$ .

Portail des mathématiques

Ce document provient de « S%C3%A9rie de Bertrand ».

Catégorie : Série

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Série de bertrand de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Serie de Bertrand — Série de Bertrand Pour α et β deux réels, on appelle série de Bertrand la série à termes réels positifs suivante : . La série harmonique en est un cas particulier (au premier terme près), pour α = 1 et β = 0 … Wikipédia en Français
Série de Bertrand — Pour α et β deux réels, on appelle série de Bertrand (du nom de Joseph Bertrand) la série à termes réels positifs suivante : Sommaire 1 Condition de convergence 1.1 Énoncé … Wikipédia en Français
Serie harmonique — Série harmonique Pour les articles homonymes, voir Série et Harmonique. En mathématiques, la série harmonique est une série de nombres réels. C est la série des inverses des entiers naturels non nuls. Sujet d étude classique en analyse, elle fait … Wikipédia en Français
Série harmonique — Pour les articles homonymes, voir Série et Harmonique. En mathématiques, la série harmonique est une série de nombres réels. C est la série des inverses des entiers naturels non nuls. Elle fait partie de la famille plus large des séries de… … Wikipédia en Français
Bertrand — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Bertrand est un nom propre qui peut désigner : Sommaire 1 Prénom et patronyme 2 Saints … Wikipédia en Français
Bertrand Russell — Saltar a navegación, búsqueda Bertrand Arthur William Russell, 3er Conde de Russell Russell en 1907 Filosofía Occidental Filosofí … Wikipedia Español
Bertrand Arthuys — (10 mai 1958 à Neuilly sur Seine) est un réalisateur et auteur français. Sommaire 1 Biographie 2 Filmographie 2.1 en tant que réalisateur … Wikipédia en Français
Bertrand Puard — Photogr. Frédéric Hébuterne Autres noms Ewan Blackshore Brad Winter Benjamin Bates … Wikipédia en Français
Bertrand Barere de Vieuzac — Bertrand Barère de Vieuzac Pour les articles homonymes, voir Vieuzac. Barère de Vieuzac … Wikipédia en Français
Bertrand Barère De Vieuzac — Pour les articles homonymes, voir Vieuzac. Barère de Vieuzac … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Série de bertrand