Règle du produit

Pour les articles homonymes, voir Règle de Leibniz.

En analyse, la règle du produit (aussi appelée règle de Leibniz, voir dérivation) est une formule utilisée afin de trouver les dérivées de produits de fonctions. On peut l'énoncer ainsi :

Soit $f$ et $g$ des fonctions différentiables en $x$ alors leur produit $(f\cdot g)$ est aussi différentiable en $x$ et

$\left(f\cdot g\right)' = f'\cdot g+f\cdot g'$

En notation de Leibniz cela revient à écrire :

${d\over dx}(f\cdot g)=f\cdot {dg\over dx}+g\cdot {df\over dx}$

Une application importante de la règle du produit est la règle d'intégration par parties.

Sommaire

1 Exemple
2 Démonstration de la règle du produit
- 2.1 Démonstration Analytique
- 2.2 Démonstration Géométrique
3 Généralisations
4 Voir aussi
5 Références

Exemple

Soit $h$ une fonction définie par :

$h\left(x\right) = (x+1)(x^2+ 1)$

Pour trouver la dérivée $h'$ de $h$ avec la règle du produit, on pose $f (x) = x + 1$ et $g (x) = (x 2 + 1)$ . Il est clair que $h$ , $f$ et $g$ sont partout dérivables.

On a alors :

$\displaystyle h'(x) = f'(x)g(x) + f(x)g'(x)$

$= \displaystyle(x^2+1) + (x+1)(2x)$

$= \displaystyle 3x^2+2x+1$

Par ailleurs, ici, on peut développer l'expression de $h$ :

$h\left(x\right) = x^3+x^2+x+1$

Expression que l'on dérive alors aisément pour retrouver :

$\displaystyle h'(x) = 3x^2+2x + 1$

Démonstration de la règle du produit

Démonstration Analytique

Une preuve rigoureuse de la règle du produit peut être donnée en utilisant les propriétés des limites et de la définition de la dérivée comme d'une limite du quotient de Newton.

Reprenons $f$ et $g$ des fonctions différentiables en $x$ , on a alors :

$(f\cdot g)'(x) = \lim_{h\to 0}\frac{f(x+h)g(x+h)-f(x)g(x)}{h}$

En ajoutant et retranchant $f (x) g (x + h)$ on obtient alors :

$= \lim_{h\to 0}\frac{f(x+h)g(x+h)-f(x)g(x+h)+f(x)g(x+h)-f(x)g(x)}{h}$

$= \lim_{h\to 0}\left(\frac{f(x+h)-f(x)}{h}g(x+h) + f(x)\frac{g(x+h)-g(x)}{h}\right)$

Comme $f$ et $g$ sont différentiables (et donc continues) en $x$ , on peut réécrire ce dernier terme comme :

$f'\left(x\right)g(x)+f(x)g'(x)$

Ce qui clôt la démonstration.

Démonstration Géométrique

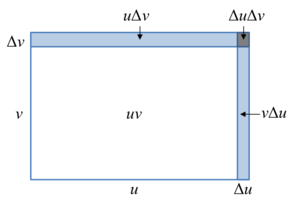
Figure 1: Illustration géométrique de la règle du produit

Soit $f$ et $g$ des fonctions différentiables en $x$ , soit encore $u = f (x)$ et $v = g (x)$ de telle sorte que l'aire $u v$ du rectangle (cf. Figure 1) représente $f (x) g (x)$ .

Si $x$ varie d'une quantité $Δ x$ , les variations correspondantes en $u$ et $v$ sont respectivement $Δ u$ et $Δ v$ .

La variation de l'aire du rectangle est alors :

$\Delta\left(uv\right) = (u+\Delta u)(v+\Delta v)-uv$

$= \left(\Delta u\right)v + u(\Delta v)+(\Delta u)(\Delta v)$

C'est-à-dire la somme des trois zones ombrées sur la Figure 1 ci-contre.

En divisant par $Δ x$ et en prenant la limite avec $\Delta x \rightarrow 0$ , on obtient :

$\frac{d}{dx}(uv) = \left(\frac{du}{dx}\right)v + u\left(\frac{dv}{dx}\right)$

Etant donné que :

$\lim_{\Delta x \to 0}\frac{\Delta u}{\Delta x}\Delta v = \frac{du}{dx}\times 0 = 0$

Cela clôt la démonstration.

Généralisations

Produit de plusieurs fonctions

Soit un ensemble $f_1, \dots, f_n$ de fonctions dérivables en $x$ , on a alors :

$\frac{d}{dx} \prod_{i=1}^n f_i(x) = \sum_{i=1}^n \left(\frac{d}{dx} f_i(x) \prod_{j\ne i} f_j(x) \right)$

Cette relation peut être démontrée par induction (voir raisonnement par récurrence).

Démonstration par induction

Pour $n = 1$ , la relation est trivialement vraie.

Nous devons maintenant montrer que si la formule est vraie pour $n=k\ge 1$ , alors elle est aussi vraie pour $n = k + 1$ .

Soit une fonction $h$ définie par :

$h(x) = \prod_{i=1}^k f_i(x)$

Avec $f_1,\dots,f_k$ des fonctions quelconques dérivables en $x$ .

Soit encore une fonction $f k + 1$ , elle-même dérivable en $x$ , la dérivée de $(h\cdot f_{k+1})$ est alors donnée par la règle du produit :

$\frac{d}{dx}\left(h(x)f_{k+1}(x)\right) = f_{k+1}'(x)h(x)+f_{k+1}(x)h'(x)$

Cela revient à écrire avec l'hypothèse de la récurrence :

$\frac{d}{dx} \prod_{i=1}^{k+1} f_i(x) = \frac{d}{dx}f_{k+1}(x)\prod_{i=1}^{k}f_i(x) + f_{k+1}(x)\sum_{i=1}^k \left(\frac{d}{dx} f_i(x) \prod_{j\ne i} f_j(x) \right)$

En simplifiant cette dernière expression on obtient finalement :

$\frac{d}{dx} \prod_{i=1}^{k+1} f_i(x) = \sum_{i=1}^{k+1} \left(\frac{d}{dx} f_i(x) \prod_{j\ne i} f_j(x) \right)$

La formule est donc aussi vraie pour

n = k + 1

. Par induction, la formule est donc vraie pour tous les entiers $n \ge 1$ .

Exemple

Avec trois fonctions $f, g$ et $h$ , dérivables en $x$ on a :

$\frac{d}{dx}(fgh) = \frac{df}{dx}gh + f\frac{dg}{dx}h + fg\frac{dh}{dx}$

Soit par exemple pour trouver la dérivée de $(x+1)(x^2+1)(\sqrt{x}-2)$ :

$\left((x+1)(x^2+1)(\sqrt{x}-2)\right)' = (x^2+1)(\sqrt{x}-2)+(x+1)(2x)(\sqrt{x}-2)+(x+1)(x^2+1)\left(\frac{1}{2\sqrt{x}}\right)$

Dérivées d'ordre supérieur (règle de Leibniz)

La règle du produit peut aussi être généralisée à la règle de Leibniz pour la dérivation d'ordre supérieur d'un produit de deux fonctions. Soit $f$ et $g$ deux fonctions n fois dérivables en $x$ l'expression de la n^ème dérivée est

$(fg)^{(n)}(x) = \sum_{i=0}^n{n \choose i}f^{(n-i)}(x)g^{(i)}(x)$

Expression dans laquelle on retrouve le coefficient binomial. Cette relation peut être démontrée par induction (voir raisonnement par récurrence). On remarque que cette expression peut être reliée à la formule du binôme de Newton (la démonstration est par ailleurs analogue).

Démonstration par induction

Par souci de lisibilité, les $(x)$ sont omis dans la démonstration.

Pour $n = 1$ , la relation donne :

$(fg)' = \sum_{i=0}^1{1 \choose i}f^{(1- i)}g^{(i)} = f'g + fg'$

C'est-à-dire la règle du produit qui a déjà été démontrée.

Nous devons maintenant montrer que si la formule est vraie pour $n = k\ge 1$ , alors elle est aussi vraie pour $n = k + 1$ .

Soit donc pour $n=k \ge 1$ :

$(fg)^{(k)} = \sum_{i=0}^k{k \choose i}f^{(k-i)}g^{(i)}$

Si l'on dérive cette expression, on obtient par la règle du produit:

$(fg)^{(k+1)} = \sum_{i=0}^k{k \choose i}f^{(k+1-i)}g^{(i)} + \sum_{i=0}^k{k \choose i}f^{(k-i)}g^{(i+1)}$

En développant ce dernier terme (pour une raison qui deviendra claire par la suite), on peut réécrire ce dernier terme comme :

$f^{(k+1)}g + \sum_{i=1}^k {k\choose i}f^{(k+1-i)}g^{(i)} + \sum_{i=0}^{k-1} {k\choose i}f^{(k-i)}g^{(i+1)} + fg^{(k+1)}$

$= f^{(k+1)}g + \sum_{i=1}^k\left({k \choose i}+{k \choose i-1}\right)f^{(k+1-i)}g^{(i)} + fg^{(k+1)}$

Cette dernière expression correspond au développement de la règle de Leibniz pour $n = k + 1$ , en effet :

$(fg)^{(k+1)} = \sum_{i=0}^{k+1}{k+1 \choose i}f^{(k+1-i)}g^{(i)}$

$= f^{(k+1)}g + \sum_{i=1}^{k}{k+1\choose i}f^{(k+1-i)}g^{(i)} + fg^{(k+1)}$

Avec

${k \choose i-1} + {k \choose i-1} = \frac{k!}{(i-1)!(k-i)!(k+1-i)} + \frac{k!}{(i-1)!i(k-i)!}$

$= \frac{k!}{(i-1)!(k-i)!}\frac{(k+1)}{(k+1-i)i} = {k+1 \choose i}$

La règle est donc aussi vraie pour

n = k + 1

. Par induction, la règle est donc vraie pour tous les entiers $n \ge 1$ .

Exemple

Avec $n = 2$ on a :

$\displaystyle (fg)''(x) = f''(x)g(x) + 2f'(x)g'(x) + f(x)g''(x)$

Soit pour trouver la dérivée seconde de $\displaystyle (x^2+1)\sin(x)$ :

$\displaystyle ((x^2+1)\sin(x))'' = 2\sin(x) + 4x\cos(x) - (x^2+1)\sin(x)$

Dimensions supérieures

On peut généraliser la règle du produit à des fonctions de dimensions supérieures : soit $U \subseteq \mathbb R^n$ un ensemble ouvert, $u, v \colon U\to\mathbb R$ des fonctions différentiables et $\mathbf x\in \mathbb R^n$ un vecteur quelconque de $\mathbb R^n$ .

La règle du produit s'écrit alors :

$\frac{\partial}{\partial\mathbf x}(uv) = \left( \frac{\partial u}{\partial\mathbf x}\right)\cdot v + u\cdot \frac{\partial v}{\partial\mathbf x}$

Fonctions holomorphes

Par analogie, la règle est applicable pour un produit de fonctions holomorphes : soit $U \subseteq \mathbb C$ et $f, g\colon U\to \mathbb C$ des fonctions holomorphes, alors $(f\cdot g)$ est holomorphe et

$\displaystyle (f\cdot g)' = f'g + fg'$ .

Règle du produit dans des espaces de Banach

Soit X, Y, et Z des espaces de Banach (ce qui inclut les espaces euclidiens) et $B : X\times Y \rightarrow Z$ un opérateur bilinéaire continu. Alors, B est différentiable et sa dérivée au point (x,y) dans $X \times Y$ est l'application linéaire $D_{(x,y)}B : X\times Y \rightarrow Z$ définie par :

$(D_\left( x,y \right)\,B)\left( u,v \right) = B\left( u,y \right) + B\left( x,v \right)\qquad\forall (u,v)\in X \times Y.$

Fonctions vectorielles

La règle du produit pour les fonctions vectorielles dont le produit est encore un vecteur doit tenir compte des propriétés anticommutatives d'un produit de vecteurs.

Soit $U \subseteq \mathbb R^n$ , un ensemble ouvert, $\mathbf f, \mathbf g \colon U\to \mathbb R^m$ des fonctions vectorielles différentiables et $\mathbf x\in \mathbb R^n$ un vecteur de $\mathbb R^n$ alors :

$(\mathbf f\mathbf g )' = \mathbf f'\mathbf g + \mathbf f\mathbf g'$

et pas

$(\mathbf f\mathbf g )' = \mathbf f'\mathbf g + \mathbf g'\mathbf f$

même si cette dernière expression est correcte dans le cas de fonctions scalaires.

Voir aussi

Références

Robert A. ADAMS; Calculus, A Complete Course, 6^th Edition, Pearson Education, 2007, ISBN 0-321-27000-2

Portail de l'analyse

Catégorie :

Dérivée

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Règle du produit de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Regle du produit — Règle du produit En analyse, la règle du produit (aussi appelée règle de Leibniz, voir dérivation) est une formule utilisée afin de trouver les dérivées de produits de fonctions. On peut l énoncer ainsi : Soit f et g des fonctions… … Wikipédia en Français
Règle de la non affectation — Principe d universalité budgétaire Le principe d universalité budgétaire est l un des quatre grands principes budgétaires des finances publiques. Les quatre principes budgétaires sont : le principe d annualité budgétaire, le principe d unité … Wikipédia en Français
Règle de non affectation — Principe d universalité budgétaire Le principe d universalité budgétaire est l un des quatre grands principes budgétaires des finances publiques. Les quatre principes budgétaires sont : le principe d annualité budgétaire, le principe d unité … Wikipédia en Français
Règle de Leibniz — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La règle de Leibniz est une règle de dérivation d un produit de fonction de la forme (fg) = f g + fg aussi appelée règle du produit. La règle de Leibniz… … Wikipédia en Français
Produit — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Produit », sur le Wiktionnaire (dictionnaire universel) Le mot produit peut avoir plusieurs… … Wikipédia en Français
Produit croisé — Règle de trois Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités … Wikipédia en Français
Produit en croix — Règle de trois Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités … Wikipédia en Français
Regle de trois — Règle de trois Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités … Wikipédia en Français
Règle de 3 — Règle de trois Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités … Wikipédia en Français
règle — [ rɛgl ] n. f. • XIIIe, adapt. du lat.; ruile 1119; reille 1105; lat. regula I ♦ (1317) Planchette allongée ou tige à arêtes rectilignes qui sert à guider le crayon, la plume, quand on trace un trait, à mesurer une longueur, etc. ⇒ réglet,… … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Règle du produit

Sommaire

Exemple