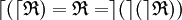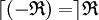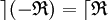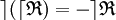- Relation ternaire interne
-
Relation ternaire interne
Une relation ternaire interne dans un ensemble associe des éléments de cet ensemble à des couples formés d’éléments de ce même ensemble.
Sommaire
Définitions
Formellement, une relation ternaire interne est une correspondance dont l’ensemble de départ est le carré cartésien de l’ensemble d’arrivée.
En d’autres termes, une relation ternaire interne
 dans un ensemble E est la somme disjointe de trois ensembles :
dans un ensemble E est la somme disjointe de trois ensembles :- un ensemble de départ, E×E ;
- un ensemble d’arrivée, E ;
- et un graphe G, inclus dans E 3, donc formé de triplets d’éléments de E.
Si x, y et z sont trois éléments de E , nous pouvons écrire que z est image par
 du couple ( x , y ) de plusieurs manières :
du couple ( x , y ) de plusieurs manières :- ( x , y , z ) ∈ G (notation ensembliste)
- ( x , y , z )
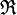 (notation relationnelle postfixée)
(notation relationnelle postfixée)
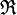 ( x , y , z ) (notation relationnelle préfixée)
( x , y , z ) (notation relationnelle préfixée)
- ( x , y )
 z (notation relationnelle infixée)
z (notation relationnelle infixée)
Nous utiliserons dans la suite cette dernière notation.
Cas particuliers :
- Une opération interne est une relation ternaire interne qui est aussi une fonction.
- Une loi de composition interne est une relation ternaire interne qui est aussi une application.
Exemples
- La relation d'équidistance dans un espace métrique, c'est-à-dire muni d'une distance d :
-
- Un point A est équidistant de deux points B et C ssi d ( A , B ) = d ( A , C )
- Ce n'est ni une opération, ni une loi de composition interne.
- L' exponentiation Exp définie par : [ ( x , y ) Exp z ] ⇔ [ z = x y ]
- C'est une opération interne dans
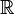 , à condition de donner un sens unique à x y quand il y a ambiguïté; ce n'est pas une loi interne dans
, à condition de donner un sens unique à x y quand il y a ambiguïté; ce n'est pas une loi interne dans 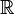 : par exemple, ( - 1 ) 1 / 2 n'a pas de sens dans
: par exemple, ( - 1 ) 1 / 2 n'a pas de sens dans 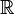 .
.
- La différence de deux ensembles Diff : [ ( A , B ) Diff C ] ⇔ [ C = A \ B ] .
- C'est une loi interne dans l'univers des ensembles, ou dans l'ensemble des parties d'un ensemble.
- Parmi les êtres humains, la relation « sont respectivement père et mère de » n'est ni une opération, ni une loi interne : un couple peut être sans enfants ou en avoir plusieurs.
- Les quatre « opérations » de notre enfance (addition, soustraction, multiplication et division) sont bien des opérations car leur résultat, quand il est défini, l'est toujours sans ambiguïté.
Propriétés
Soit un ensemble E muni d’une relation ternaire interne
 . Remarques :
. Remarques :- Les propriétés suivantes s’appliquent évidemment aussi aux lois de composition internes, mais sous une forme simplifiée par l'emploi d'une notation fonctionnelle (z = f ( x, y ) ou z = x
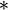 y ).
y ). - Attention : un couple peut très bien avoir plusieurs images par
 .
. - La liste de propriétés qui suit n’est pas exhaustive.
Existence d’éléments remarquables
 est idempotente si et seulement si tout élément x de E est image par
est idempotente si et seulement si tout élément x de E est image par  du couple ( x , x )
du couple ( x , x )
- ou :
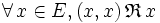
 est dévolutive si et seulement s’il existe un élément de E image par
est dévolutive si et seulement s’il existe un élément de E image par  de tout couple de la diagonale de E
de tout couple de la diagonale de E
- ou :
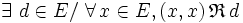
 est unifère à gauche si et seulement s’il existe un élément de E tel que tout couple dont il est la première composante a pour image par
est unifère à gauche si et seulement s’il existe un élément de E tel que tout couple dont il est la première composante a pour image par  sa seconde composante
sa seconde composante
- ou :
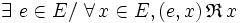
 est unifère à droite si et seulement s’il existe un élément de E tel que tout couple dont il est la seconde composante a pour image par
est unifère à droite si et seulement s’il existe un élément de E tel que tout couple dont il est la seconde composante a pour image par  sa première composante
sa première composante
- ou :
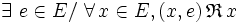
 est unifère si et seulement si elle est unifère à gauche et à droite avec le même élément neutre.
est unifère si et seulement si elle est unifère à gauche et à droite avec le même élément neutre.
 est absorbante à gauche si et seulement s’il existe un élément de E tel que tout couple dont il est la première composante l’a pour image par
est absorbante à gauche si et seulement s’il existe un élément de E tel que tout couple dont il est la première composante l’a pour image par 
- ou :
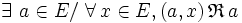
 est absorbante à droite si et seulement s’il existe un élément de E tel que tout couple dont il est la seconde composante l’a pour image par
est absorbante à droite si et seulement s’il existe un élément de E tel que tout couple dont il est la seconde composante l’a pour image par 
- ou :
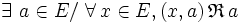
 est absorbante si et seulement si elle est absorbante à gauche et à droite avec le même élément absorbant.
est absorbante si et seulement si elle est absorbante à gauche et à droite avec le même élément absorbant.
 est involutive à gauche si et seulement si elle est dévolutive et unifère à gauche avec l’élément dévolutif pour élément neutre.
est involutive à gauche si et seulement si elle est dévolutive et unifère à gauche avec l’élément dévolutif pour élément neutre.
 est involutive à droite si et seulement si elle est dévolutive et unifère à droite avec l’élément dévolutif pour élément neutre.
est involutive à droite si et seulement si elle est dévolutive et unifère à droite avec l’élément dévolutif pour élément neutre.
 est involutive si et seulement si elle est involutive à gauche et à droite avec le même élément involutif.
est involutive si et seulement si elle est involutive à gauche et à droite avec le même élément involutif.
 est nilpotente à gauche si et seulement si elle est dévolutive et absorbante à gauche avec l’élément dévolutif pour élément absorbant.
est nilpotente à gauche si et seulement si elle est dévolutive et absorbante à gauche avec l’élément dévolutif pour élément absorbant.
 est nilpotente à droite si et seulement si elle est dévolutive et absorbante à droite avec l’élément dévolutif pour élément absorbant.
est nilpotente à droite si et seulement si elle est dévolutive et absorbante à droite avec l’élément dévolutif pour élément absorbant.
 est nilpotente si et seulement si elle est nilpotente à gauche et à droite avec le même élément nilpotent.
est nilpotente si et seulement si elle est nilpotente à gauche et à droite avec le même élément nilpotent.
Régularité et propriétés apparentées
 est régulière à gauche si et seulement si pour toute paire de couples distincts d’éléments de E de même première composante, les deux couples n’ont pas d’image commune par
est régulière à gauche si et seulement si pour toute paire de couples distincts d’éléments de E de même première composante, les deux couples n’ont pas d’image commune par 
- ou :
![\forall ( x , y , z , t ) \in E^{\, 4} , [ ( x , z ) \mathfrak{R} \, t \wedge ( x , y ) \mathfrak{R} \, t ] \Rightarrow [ z = y ] \,](/pictures/frwiki/53/549f28404efae22a121c59b8bbce5754.png)
 est régulière à droite si et seulement si pour toute paire de couples distincts d'éléments de E de même seconde composante, les deux couples n'ont pas d'image commune par
est régulière à droite si et seulement si pour toute paire de couples distincts d'éléments de E de même seconde composante, les deux couples n'ont pas d'image commune par 
- ou :
![\forall ( x , y , z , t ) \in E^{\, 4} , [ ( x , z ) \mathfrak{R} \, t \wedge ( y , z ) \mathfrak{R} \, t ] \Rightarrow [ x = y ] \,](/pictures/frwiki/48/03287cd94ae9ea382465cbba1b588fae.png)
 est régulière si et seulement si elle est régulière à gauche et à droite.
est régulière si et seulement si elle est régulière à gauche et à droite.
 est antirégulière si et seulement si pour toute paire de couples non réciproques d'éléments de E dont la première composante de l'un est égale à la seconde composante de l'autre, les deux couples n'ont pas d'image commune par
est antirégulière si et seulement si pour toute paire de couples non réciproques d'éléments de E dont la première composante de l'un est égale à la seconde composante de l'autre, les deux couples n'ont pas d'image commune par 
- ou :
![\forall ( x , y , z , t ) \in E^{\, 4} , [ ( x , z ) \mathfrak{R} \, t \wedge ( y , x ) \mathfrak{R} \, t ] \Rightarrow [ z = y ] \,](/pictures/frwiki/55/7b8e06ab3a08249344708d75e66aabf3.png)
Associativité et propriétés analogues
 est associative si et seulement si elle vérifie la propriété suivante :
est associative si et seulement si elle vérifie la propriété suivante :
 est associative des puissances si et seulement si elle vérifie la propriété suivante :
est associative des puissances si et seulement si elle vérifie la propriété suivante :
 est permutative si et seulement si elle vérifie la propriété suivante :
est permutative si et seulement si elle vérifie la propriété suivante :
Autres propriétés
 est commutative si et seulement si toute image par
est commutative si et seulement si toute image par  d'un couple est aussi image du couple réciproque
d'un couple est aussi image du couple réciproque
- ou :
![\forall ( x , y , z ) \in E^{\, 3} , [ ( x , y ) \mathfrak{R} \, z ] \Rightarrow [ ( y , x ) \mathfrak{R} \, z ] \,](/pictures/frwiki/51/38f24df8c6644fc316deef9c9a46eecb.png)
- Remarque : toute relation ternaire interne commutative est aussi associative des puissances.
Exemples
- la relation d'équidistance est commutative, dévolutive et idempotente;
- l'exponentiation est unifère à droite, mais pas à gauche, d'élément neutre 1; elle est absorbante à gauche, mais pas à droite, d'élément absorbant 1; elle est régulière à droite, mais pas à gauche;
- la relation "sont respectivement père et mère de" est régulière;
- la relation de concaténation des mots est associative, unifère d'élément neutre le mot vide "", et régulière;
Relation ternaire opposée
Définition et exemples
Soit un ensemble E muni d'une relation ternaire interne
 .
.La relation ternaire opposée à
 est la relation ternaire interne notée « -
est la relation ternaire interne notée « -  » , et définie par :
» , et définie par :Par exemple, la relation opposée à l' exponentiation Exp définie par : [ ( x , y ) Exp z ] ⇔ [ z = x y ] est la relation z = y x .
Un autre exemple est la différence de deux ensembles Diff : [ ( A , B ) Diff C ] ⇔ [ C = A \ B ] .
Sa relation opposée est définie par [ ( A , B ) (-Diff) C ] ⇔ [ C = B \ A ].Ou encore, parmi les êtres humains, la relation « sont respectivement père et mère de » a pour opposée la relation « sont respectivement mère et père de ».
Propriétés
- Chaque relation ternaire interne a une relation opposée et une seule.
- Toute relation ternaire est l'opposée de son opposée.
- L'opposée d'une relation ternaire est une opération si et seulement si cette relation est une opération.
- L'opposée d'une relation ternaire est une loi de composition si et seulement si cette relation est une loi de composition.
- Une relation ternaire se confond avec son opposée si et seulement si elle est commutative.
Relations ternaires inverses
Présentation
Inverser une relation, c'est en quelque sorte en "inverser" les effets : par exemple, inverser une addition, où on a ajouté quelque chose, c'est retrancher de la somme ce qui a été ajouté, donc effectuer une soustraction. Il s'agit donc essentiellement de changer l'ordre des termes impliqués dans la relation.
De manière plus précise, inverser une relation, c'est permuter les composantes des n-uplets de son graphe, de la même manière pour tous les n-uplets, de sorte que les dernières composantes (les images), en deviennent les premières composantes.
Pour une relation binaire, dont les éléments du graphe sont des couples, cela revient à permuter les deux composantes de chacun de ces couples, c'est-à-dire à remplacer chaque couple par son réciproque; en résumé, la relation inverse d'une relation binaire n'est autre que sa relation réciproque.
Pour une relation ternaire, dont les éléments du graphe sont des triplets, inverser cette relation revient à permuter les composantes de ces triplets de sorte que la dernière composante devienne la première. Il reste deux façons de disposer les deux autres composantes, d'où a priori deux relations inverses. On appellera l'une relation inverse à gauche et l'autre relation inverse à droite.
Pour une relation n-aire, on dénombre ainsi (n - 1)! relations inverses a priori distinctes. On peut remarquer que toutes ces relations inverses sont de même arité intrinsèque que la relation qui leur a donné naissance.
Définitions et exemples
Soit un ensemble E muni d'une relation ternaire interne
 .
.La relation ternaire inverse à gauche ( ou RTIG) de la relation
 est la relation ternaire interne notée «
est la relation ternaire interne notée « 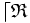 » , et définie par :
» , et définie par :La relation ternaire inverse à droite ( ou RTID) de la relation
 est la relation ternaire interne notée «
est la relation ternaire interne notée « 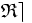 » ou «
» ou « 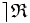 », et définie par :
», et définie par :Pour clarifier ces notions reprenons l'exemple de l'exponentiation Exp.
- Sa RTIG est définie par : z = x 1/y ; autrement dit, c'est la racine y-ième de x;
- Sa RTID est définie par : z = log y x ; autrement dit, c'est le logarithme en base y de x.
Si
 est commutative, sa RTIG et sa RTID se confondent en une seule relation ternaire inverse (RTI) notée «
est commutative, sa RTIG et sa RTID se confondent en une seule relation ternaire inverse (RTI) notée « 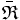 ».
».Exemples :
- la soustraction est la RTI de l'addition;
- la division est la RTI de la multiplication;
Ces exemples montrent qu'en général les RTI ne sont pas commutatives; sauf exception, elles n'ont donc pas elles-mêmes de RTI, seulement une RTIG et une RTID distinctes, la RTIG n'étant autre que la relation ternaire initiale, et la RTID l'opposée de la RTI.
Ainsi, la soustraction, non commutative, a pour RTIG l'addition et pour RTID la relation opposée à la soustraction. Cette dernière, par ailleurs, a pour RTID l'addition et pour RTIG la soustraction.
Propriétés
- Toute relation ternaire interne est la RTIG de sa RTIG, et la RTID de la RTID de sa RTID.
- La RTIG de l'opposée d'une relation ternaire est la RTID de cette dernière.
- La RTID de l'opposée d'une relation ternaire est la RTIG de cette dernière.
- La RTID de la RTIG d'une relation ternaire interne est la relation opposée à sa RTID.
- La RTID de la RTID d'une relation ternaire interne est la relation opposée à sa RTIG.
Dans les propriétés précédentes, des symétries apparaissent. Plus précisément, il est possible d'importer sur l'ensemble
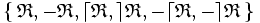 la structure du groupe des permutations à 3 éléments (
la structure du groupe des permutations à 3 éléments (  joue alors le rôle de l'élément neutre ).
joue alors le rôle de l'élément neutre ). est régulière à gauche si et seulement si sa RTIG est une opération interne.
est régulière à gauche si et seulement si sa RTIG est une opération interne.
 est régulière à droite si et seulement si sa RTID est une opération interne.
est régulière à droite si et seulement si sa RTID est une opération interne.
- Si
 est commutative, alors elle est régulière si et seulement si sa RTI est une opération interne.
est commutative, alors elle est régulière si et seulement si sa RTI est une opération interne.
- Si
 est commutative, unifère et inversible, alors sa RTI est une loi de composition interne.
est commutative, unifère et inversible, alors sa RTI est une loi de composition interne.
 est dévolutive si et seulement si sa RTIG est unifère à gauche , et cette RTIG l'est si et seulement si la RTID l'est aussi.
est dévolutive si et seulement si sa RTIG est unifère à gauche , et cette RTIG l'est si et seulement si la RTID l'est aussi.
 est unifère à gauche si et seulement si sa RTIG est dévolutive, et cette RTIG l'est si et seulement si la RTID est unifère à droite.
est unifère à gauche si et seulement si sa RTIG est dévolutive, et cette RTIG l'est si et seulement si la RTID est unifère à droite.
 est unifère à droite si et seulement si sa RTIG est unifère à droite, et cette RTIG l'est si et seulement si la RTID est dévolutive.
est unifère à droite si et seulement si sa RTIG est unifère à droite, et cette RTIG l'est si et seulement si la RTID est dévolutive.
- Si
 est commutative, alors elle est unifère si et seulement si sa RTI est dévolutive et unifère à droite, c'est-à-dire involutive à droite.
est commutative, alors elle est unifère si et seulement si sa RTI est dévolutive et unifère à droite, c'est-à-dire involutive à droite.
 est permutative si et seulement si sa RTIG l'est aussi, et cette RTIG est permutative si et seulement si la RTID l'est aussi.
est permutative si et seulement si sa RTIG l'est aussi, et cette RTIG est permutative si et seulement si la RTID l'est aussi.
Exemples :
- (
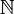 , + ) est un semigroupe; par conséquent, la soustraction est dans
, + ) est un semigroupe; par conséquent, la soustraction est dans 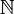 une opération interne permutative, régulière et involutive à droite d'élément neutre 0;
une opération interne permutative, régulière et involutive à droite d'élément neutre 0; - de même, (
 *, x ) est un semigroupe, d'où la division dans
*, x ) est un semigroupe, d'où la division dans  * est une opération interne permutative, régulière et involutive à droite d'élément neutre 1;
* est une opération interne permutative, régulière et involutive à droite d'élément neutre 1; - (
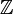 , + ) est un groupe abélien; par conséquent, la soustraction est dans
, + ) est un groupe abélien; par conséquent, la soustraction est dans 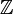 une loi interne permutative, régulière et involutive à droite d'élément neutre 0, c'est-à-dire que (
une loi interne permutative, régulière et involutive à droite d'élément neutre 0, c'est-à-dire que ( 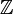 , - ) est un antigroupe;
, - ) est un antigroupe; - de même, (
 *, x ) est un groupe abélien, d'où la division dans
*, x ) est un groupe abélien, d'où la division dans  * est une loi interne permutative, régulière et involutive à droite d'élément neutre 1, c'est-à-dire que (
* est une loi interne permutative, régulière et involutive à droite d'élément neutre 1, c'est-à-dire que ( 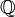 *, / ) est aussi un antigroupe.
*, / ) est aussi un antigroupe.
Voir aussi
- Portail des mathématiques
Catégorie : Théorie des ensembles
Wikimedia Foundation. 2010.

![\forall ( u , v , w , x , y , z ) \in E^{\, 6} , [ ( x , y ) \mathfrak{R} \, u \wedge ( u , z ) \mathfrak{R} \, w \wedge ( y , z ) \mathfrak{R} \, v ] \Rightarrow [ ( x , v ) \mathfrak{R} \, w ] \,](/pictures/frwiki/57/940aee35b1f55538fe40ca42ff68d6ff.png)
![\forall ( x , y , z ) \in E^{\, 3} , [ ( x , x ) \mathfrak{R} \, y \wedge ( x , y ) \mathfrak{R} \, z ] \Rightarrow [ ( y , x ) \mathfrak{R} \, z ] \,](/pictures/frwiki/53/5c428cff4b1bfe141f5d15654aea89f1.png)
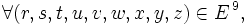
![[ ( x , y ) \mathfrak{R} \, z \wedge ( u , v ) \mathfrak{R} \, w \wedge ( x , u ) \mathfrak{R} \, r \wedge ( y , v ) \mathfrak{R} \, s \wedge ( z , w ) \mathfrak{R} \, t ] \Rightarrow [ ( r , s ) \mathfrak{R} \, t ] \,](/pictures/frwiki/98/bc7737d69c6da100dc4200b465b62d96.png)
![\forall ( x , y , z ) \in E^{\, 3} , [ ( x , y ) (-\mathfrak{R}) \, z ] \Leftrightarrow [ ( y , x ) \mathfrak{R} \, z ] \,](/pictures/frwiki/51/3d05487dc3bc76510b13dcc7fca10887.png)
![\forall ( x , y , z ) \in E^{\, 3} , [ ( x , y ) \lceil \mathfrak{R} \, z ] \Leftrightarrow [ ( z , y ) \mathfrak{R} \, x ] \,](/pictures/frwiki/50/2f55c9f753ba5ccc9a45a2bdf1279405.png)
![\forall ( x , y , z ) \in E^{\, 3} , [ ( x , y ) \mathfrak{R} \rceil \, z ] \Leftrightarrow [ ( y , z ) \mathfrak{R} \, x ] \,](/pictures/frwiki/55/74313d885ba31f7bd8bc08922c4ba37d.png)