Relation ternaire externe

Une relation ternaire externe dans un ensemble associe des éléments de cet ensemble à des couples dont une composante vient de cet ensemble et l'autre d'un ensemble dit de scalaires ou d' opérateurs.

Sommaire

1 Définitions
2 Principales propriétés
3 Relation ternaire opposée
- 3.1 Définition
4 Propriétés
5 Relations inverses
- 5.1 Définitions
- 5.2 Propriétés
6 Voir aussi

Définitions

Dans ce qui précède, une question se pose : les scalaires forment-ils la première ou la seconde composante des couples concernés ? Pour lever cette ambiguïté, il faut distinguer entre relations ternaires externes à gauche et à droite.

Plus précisément, une relation ternaire externe à gauche 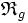$\mathfrak{R}_g$ dans un ensemble E à opérateurs (ou scalaires) dans un ensemble S, ou plus brièvement relation ternaire à gauche de S dans E , est une correspondance de S×E dans E, c'est-à-dire la somme disjointe des trois ensembles suivants :

l'ensemble de départ S×E;
l'ensemble d'arrivée E;
et un graphe G inclus dans S×E ² , donc formé de triplets dont la première composante est scalaire et les deux autres sont des éléments de E.

Si λ est un élément de S, c'est-à-dire un scalaire, et x et y deux éléments de E, nous pouvons écrire que y est image par 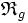$\mathfrak{R}_g$ du couple ( λ , x ) de plusieurs manières :

( λ , x , y ) ∈ G ( notation ensembliste )
( λ , x , y ) 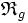$\mathfrak{R}_g$ ( notation relationnelle postfixée )
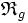$\mathfrak{R}_g$ ( λ , x , y ) ( notation relationnelle préfixée )
( λ , x ) 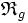$\mathfrak{R}_g$ y ( notation relationnelle infixée )

Nous utiliserons dans la suite cette dernière notation.

Symétriquement, une relation ternaire externe à droite 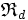$\mathfrak{R}_d$ dans un ensemble E à opérateurs (ou scalaires) dans un ensemble S, ou plus brièvement relation ternaire à droite de S dans E , est une correspondance de E×S dans E, c'est-à-dire la somme disjointe des trois ensembles suivants :

l'ensemble de départ E×S;
l'ensemble d'arrivée E;
et un graphe G inclus dans E×S×E, donc formé de triplets dont la deuxième composante est scalaire et les deux autres sont des éléments de E.

Si λ est un élément de S, c'est-à-dire un scalaire, et x et y deux éléments de E, nous pouvons écrire que y est image par 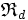$\mathfrak{R}_d$ du couple ( x , λ ) de plusieurs manières :

( x , λ , y ) ∈ G ( notation ensembliste )
( x , λ , y ) 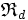$\mathfrak{R}_d$ ( notation relationnelle postfixée )
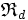$\mathfrak{R}_d$ ( x , λ , y ) ( notation relationnelle préfixée )
( x , λ ) 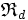$\mathfrak{R}_d$ y ( notation relationnelle infixée )

Là encore, nous utiliserons dans la suite cette dernière notation.

Cas particuliers :

Une opération externe est une relation ternaire externe qui est aussi une fonction.
Une loi de composition externe est une relation ternaire externe qui est aussi une application.

Principales propriétés

Soit un ensemble E muni d'une relation ternaire externe 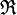$\mathfrak{R}$ sur un ensemble S de scalaires. Nous considérerons le cas d'une relation à gauche (resp. à droite).

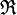$\mathfrak{R}$ est exo-unifère à gauche ( resp. exo-unifère à droite ), ou plus simplement unifère ssi il existe un élément de S tel que tout couple dont il est la première composante ( resp. la seconde ) a pour image par 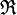$\mathfrak{R}$ sa seconde ( resp. sa première ) composante

ou :

- pour une relation à gauche :

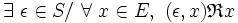
$\exists\ \epsilon \in S /\ \forall\ x \in E ,\ ( \epsilon , x ) \mathfrak{R} x \,$

- et à droite :

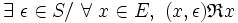
$\exists\ \epsilon \in S /\ \forall\ x \in E ,\ ( x , \epsilon ) \mathfrak{R} x \,$

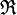$\mathfrak{R}$ est absorbante à droite ( resp. absorbante à gauche ), ou plus simplement absorbante ssi il existe un élément de E tel que tout couple dont il est la seconde composante ( resp. la première ) l'a pour image par $\mathfrak{R}$

ou :

- pour une relation à gauche :

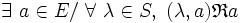
$\exists\ a \in E /\ \forall\ \lambda \in S ,\ ( \lambda , a ) \mathfrak{R} a \,$

- et à droite :

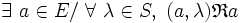
$\exists\ a \in E /\ \forall\ \lambda \in S ,\ ( a , \lambda ) \mathfrak{R} a \,$

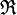$\mathfrak{R}$ est exo-absorbante à gauche ( resp. exo-absorbante à droite ), ou plus simplement exo-absorbante ssi il existe un élément de E et un élément de S tels que tout couple dont l'élément de S est la première composante ( resp. la seconde ) a pour image par $\mathfrak{R}$ l'élément de E

ou :

- pour une relation à gauche :

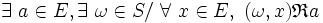
$\exists\ a \in E , \exists\ \omega \in S /\ \forall\ x \in E ,\ ( \omega , x ) \mathfrak{R} a \,$

- et à droite :

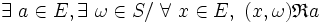
$\exists\ a \in E , \exists\ \omega \in S /\ \forall\ x \in E ,\ ( x , \omega ) \mathfrak{R} a \,$

$\mathfrak{R}$ est régulière à gauche ( resp. à droite ) ssi aucun couple de S × E ( resp. E × S ) n'a d'image commune avec un autre couple de S × E ( resp. E × S ) de même première ( resp. seconde ) composante

ou :

- pour une relation à gauche :

$\forall\ \lambda \in S , \forall\ ( x , y , z ) \in E^3 , [\ ( \lambda , x ) \mathfrak{R} z \ \wedge\ ( \lambda , y ) \mathfrak{R} z \ ] \Rightarrow ( x = y ) \,$

- et à droite :

$\forall\ \lambda \in S , \forall\ ( x , y , z ) \in E^3 , [\ ( x , \lambda ) \mathfrak{R} z \ \wedge\ ( y , \lambda ) \mathfrak{R} z \ ] \Rightarrow ( x = y ) \,$

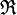$\mathfrak{R}$ est exo-régulière à droite ( resp. à gauche ) ssi aucun couple de S × E ( resp. E × S ) n'a d'image commune avec un autre couple de S × E ( resp. E × S ) de même seconde ( resp. première ) composante

ou :

- pour une relation à gauche :

$\forall\ ( \lambda , \mu ) \in S^2 , \forall\ ( x , y ) \in E^2 , [\ ( \lambda , x ) \mathfrak{R} y \ \wedge\ ( \mu , x ) \mathfrak{R} y \ ] \Rightarrow ( \lambda = \mu ) \,$

- et à droite :

$\forall\ ( \lambda , \mu ) \in S^2 , \forall\ ( x , y ) \in E^2 , [\ ( x , \lambda ) \mathfrak{R} y \ \wedge\ ( x , \mu ) \mathfrak{R} y \ ] \Rightarrow ( \lambda = \mu ) \,$

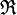$\mathfrak{R}$ est régulière ssi elle est régulière d'un côté et exo-régulière de l'autre.

Relation ternaire opposée

Définition

Soit un ensemble E muni d'une relation ternaire externe 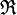$\mathfrak{R}$ sur un ensemble S de scalaires.

La relation ternaire opposée à 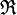$\mathfrak{R}$ est la relation ternaire externe notée « - 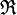$\mathfrak{R}$ » et définie par :

- si la relation est à gauche :

$\forall\ \lambda \in S , \forall\ ( x , y ) \in E^2 , \ [ \ ( x , \lambda ) ( - \mathfrak{R} ) y \ ] \Leftrightarrow [ \ ( \lambda , x ) \mathfrak{R} y \ ] \,$

- si la relation est à droite :

$\forall\ \lambda \in S , \forall\ ( x , y ) \in E^2 , \ [ \ ( \lambda , x ) ( - \mathfrak{R} ) y \ ] \Leftrightarrow [ \ ( x , \lambda ) \mathfrak{R} y \ ] \,$

Propriétés

Chaque relation ternaire externe a une relation opposée et une seule.
La relation opposée d'une relation ternaire externe à gauche est une relation à droite, et vice versa.
Toute relation ternaire est l'opposée de son opposée.
L'opposée d'une relation ternaire est une opération ssi cette relation est une opération.
L'opposée d'une relation ternaire est une loi de composition ssi cette relation est une loi de composition.
Une relation ternaire externe n'est jamais égale à son opposée ( hormis le cas d'une relation interne , mais il s'agit alors d'un abus de langage ).

Relations inverses

Définitions

Soit un ensemble E muni d'une relation ternaire externe à gauche ( resp. à droite ) 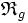$\mathfrak{R}_g$ ( resp. 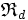$\mathfrak{R}_d$ ) sur un ensemble S de scalaires.

La relation inverse à gauche ( resp. à droite ) ( ou RIG ( resp. RID )) de la relation 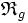$\mathfrak{R}_g$ ( resp. 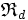$\mathfrak{R}_d$ ) est la relation scalaire de E × E dans S notée « 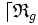$\lceil \mathfrak{R}_g$ » ( resp. « 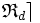$\mathfrak{R}_d \rceil$ » ), et définie par :

$\forall\ \lambda \in S , \forall\ ( x , y ) \in E^2 ,\ [\ ( x , y ) \lceil \mathfrak{R}_g \lambda\ ] \Leftrightarrow [\ ( \lambda , y ) \mathfrak{R}_g x \ ] \,$

ou resp. pour une relation à droite par :

$\forall\ \lambda \in S , \forall\ ( x , y ) \in E^2 ,\ [\ ( x , y ) \mathfrak{R}_d \rceil \lambda\ ] \Leftrightarrow [\ ( y , \lambda ) \mathfrak{R}_d x \ ] \,$

La relation ternaire inverse à droite ( resp. à gauche ) ( ou RTID ( resp. RTIG ) de la relation 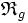$\mathfrak{R}_g$ ( resp. 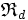$\mathfrak{R}_d$ ) est la relation ternaire externe à droite notée « 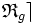$\mathfrak{R}_g \rceil$ » ( resp. « 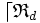$\lceil \mathfrak{R}_d$ » ), et définie par :

$\forall\ \lambda \in S , \forall\ ( x , y ) \in E^2 ,\ [\ ( x , \lambda ) \mathfrak{R}_g \rceil y \ ] \Leftrightarrow [\ ( \lambda , y ) \mathfrak{R}_g x \ ] \,$

ou resp. pour une relation à droite par :

$\forall\ \lambda \in S , \forall\ ( x , y ) \in E^2 ,\ [\ ( x , \lambda ) \lceil \mathfrak{R}_d y \ ] \Leftrightarrow [\ ( y , \lambda ) \mathfrak{R}_d x \ ] \,$

Ces définitions peuvent sembler à première vue arbitraires, mais elles sont telles qu'elles coïncident avec les définitions des relations inverses pour les relations ternaires internes, dans le cas où S = E.

Propriétés

Toute relation ternaire externe à droite est la RTIG de sa RTIG.

La RTIG de l'opposée d'une relation ternaire externe à gauche est la RTID de cette dernière.
La RID de l'opposée d'une relation ternaire externe à gauche est la RIG de cette dernière, et c'est une relation scalaire.

La RTID de l'opposée d'une relation ternaire externe à droite est la RTIG de cette dernière.
La RIG de l'opposée d'une relation ternaire externe à droite est la RID de cette dernière, et c'est une relation scalaire.

Voir aussi

Portail des mathématiques

Ce document provient de « Relation ternaire externe ».

Catégorie : Théorie des ensembles

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Relation ternaire externe de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Relation scalaire — Une relation scalaire est une correspondance dont l ensemble de départ est le carré cartésien d un ensemble de base E. L ensemble d arrivée de cette correspondance est alors considéré comme un ensemble de scalaires S sur l ensemble E. Sommaire 1… … Wikipédia en Français
Relation (mathematiques) — Correspondance et relation En algèbre générale (ou abstraite), le concept de correspondance, ou de relation, est une abstraction de notions telles que l’égalité, l’ordre alphabétique, ou la comparaison. De manière informelle, une relation dans un … Wikipédia en Français
Relation mathématique — Correspondance et relation En algèbre générale (ou abstraite), le concept de correspondance, ou de relation, est une abstraction de notions telles que l’égalité, l’ordre alphabétique, ou la comparaison. De manière informelle, une relation dans un … Wikipédia en Français
RELATION — Le concept de relation apparaît comme l’un des concepts fondamentaux du discours rationnel. Il semble lié à la pratique de l’analyse, qui constitue elle même l’un des aspects essentiels de la démarche discursive. L’analyse décompose les unités… … Encyclopédie Universelle
Correspondance Et Relation — En algèbre générale (ou abstraite), le concept de correspondance, ou de relation, est une abstraction de notions telles que l’égalité, l’ordre alphabétique, ou la comparaison. De manière informelle, une relation dans un ensemble ( on dit aussi… … Wikipédia en Français
Correspondance et relation — En algèbre générale (ou abstraite), le concept de correspondance, ou de relation, est une abstraction de notions telles que l’égalité, l’ordre alphabétique, ou la comparaison. De manière informelle, une relation dans un ensemble ( on dit aussi… … Wikipédia en Français
Graphe d'une relation — Correspondance et relation En algèbre générale (ou abstraite), le concept de correspondance, ou de relation, est une abstraction de notions telles que l’égalité, l’ordre alphabétique, ou la comparaison. De manière informelle, une relation dans un … Wikipédia en Français
Loi De Composition Externe — En mathématiques, une loi de composition externe dans un ensemble E à opérateurs (ou scalaires) dans S ( on dit aussi plus brièvement une loi externe de S sur E ) est une relation ternaire externe de S sur E qui est aussi une application.… … Wikipédia en Français
Loi de composition externe — En mathématiques, une loi de composition externe dans un ensemble E à opérateurs (ou scalaires) dans S ( on dit aussi plus brièvement une loi externe de S sur E ) est une relation ternaire externe de S sur E qui est aussi une application.… … Wikipédia en Français
Loi externe — Loi de composition externe En mathématiques, une loi de composition externe dans un ensemble E à opérateurs (ou scalaires) dans S ( on dit aussi plus brièvement une loi externe de S sur E ) est une relation ternaire externe de S sur E qui est… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Relation ternaire externe