- Relation scalaire
-
Relation scalaire
Une relation scalaire est une correspondance dont l' ensemble de départ est le carré cartésien d'un ensemble de base E. L' ensemble d'arrivée de cette correspondance est alors considéré comme un ensemble de scalaires S sur l'ensemble E.
Sommaire
Définitions et exemples
Soient E un ensemble dont les éléments sont notés par des lettres latines minuscules ( x , y , z ,... ), et S un autre ensemble dont les éléments sont notés par des lettres grecques minuscules ( λ , μ , ν ,... ).
Une relation scalaire
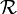 de E dans S est une correspondance de E 2 dans S :
de E dans S est une correspondance de E 2 dans S :Le graphe G de la relation scalaire
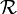 est parfois appelé graphe de E valué à valeurs dans S.
est parfois appelé graphe de E valué à valeurs dans S.Les produits scalaires ou les distances sont des exemples de relations scalaires.
Un carré est un couple appartenant à la diagonale de E, c'est-à-dire un couple de la forme ( x , x ) où x appartient à E.
Principales propriétés
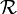 est dite fonctionnelle si tout couple de E 2 a au plus une image par
est dite fonctionnelle si tout couple de E 2 a au plus une image par 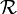 , c'est-à-dire si :
, c'est-à-dire si :
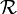 est dite applicative si tout couple de E 2 a au moins une image par
est dite applicative si tout couple de E 2 a au moins une image par 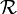 , c'est-à-dire si :
, c'est-à-dire si :
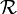 est dite dévolutive si tous les carrés dans E ont une image commune par
est dite dévolutive si tous les carrés dans E ont une image commune par 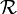 , c'est-à-dire si :
, c'est-à-dire si :
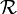 est dite commutative si chaque couple de E 2 a ses images par
est dite commutative si chaque couple de E 2 a ses images par 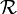 en commun avec son couple réciproque, c'est-à-dire si :
en commun avec son couple réciproque, c'est-à-dire si :
Relation opposée
La relation scalaire opposée à la relation scalaire
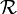 est la relation scalaire notée « -
est la relation scalaire notée « - 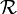 » définie par :
» définie par :- Toute relation scalaire est l'opposée de son opposée.
- Une relation scalaire se confond avec son opposée ssi elle est commutative.
Relations inverses
Toute relation scalaire a une et une seule RTIG (relation ternaire inverse à gauche) , notée «
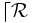 » , et définie par :
» , et définie par :
Toute relation scalaire a une et une seule RTID (relation ternaire inverse à droite)) , notée «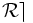 » , et définie par :
» , et définie par :Voir aussi
- Portail des mathématiques
Catégorie : Vocabulaire des mathématiques
Wikimedia Foundation. 2010.

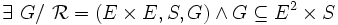
![\forall\ ( x , y ) \in E^2 , \forall\ ( \lambda , \mu ) \in S^2 ,\ [ \ ( x , y ) \mathcal R \lambda \ \wedge \ ( x , y ) \mathcal R \mu \ ] \Rightarrow [ \ \lambda = \mu \ ] \,](/pictures/frwiki/52/492704747f20b54670ef4ec5ad9017db.png)
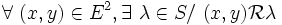
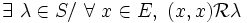
![\forall\ ( x , y ) \in E^2 , \forall\ \lambda \in S ,\ [ \ ( x , y ) \mathcal R \lambda \ ] \Rightarrow [ \ ( y , x ) \mathcal R \lambda \ ] \,](/pictures/frwiki/56/8e88c88f110b576d56c6aad18c1ac53e.png)
![\forall\ ( x , y ) \in E^2 , \forall\ \lambda \in S ,\ [ \ ( x , y ) ( - \mathcal R ) \lambda \ ] \Leftrightarrow [ \ ( y , x ) \mathcal R \lambda \ ] \,](/pictures/frwiki/48/083f1719425e1466985ad803615c39e2.png)
![\forall\ ( x , y ) \in E^2 , \forall\ \lambda \in S ,\ [ \ ( \lambda , x ) ( \lceil \mathcal R ) y \ ] \Leftrightarrow [ \ ( y , x ) \mathcal R \lambda \ ] \,](/pictures/frwiki/57/9305090c6b7b5e961f8b3c22aae830ba.png)
![\forall\ ( x , y ) \in E^2 , \forall\ \lambda \in S ,\ [ \ ( \lambda , x ) ( \mathcal R \rceil ) y \ ] \Leftrightarrow [ \ ( x , y ) \mathcal R \lambda \ ] \,](/pictures/frwiki/55/74015f412384e8f770d531c26f9c74d2.png)