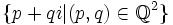- Rationnels de Gauss
-
Rationnel de Gauss
En mathématiques, un rationnel de Gauss est un nombre complexe dont les parties réelle et imaginaire sont des nombres rationnels. L'ensemble des rationnels de Gauss, muni de l'addition et de la multiplication usuelles des nombres complexes, est un corps, généralement noté
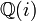 .
.De manière formelle, les rationnels de Gauss forment l'ensemble :
Les rationnels de Gauss tirent leur nom du mathématicien allemand Carl Friedrich Gauss.
Propriétés
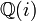 est un corps quadratique de discriminant -4.
est un corps quadratique de discriminant -4.En effet, l'ensemble des rationnels de Gauss correspond à l'extension quadratique du polynôme X2 + 1. Comme ce polynôme est irréductible sur l'ensemble des rationnels, le quotient de l'anneau des polynômes à coefficients rationnels par l'idéal engendré par le polynôme est naturellement muni d'une structure de corps.
Dans le cas d'une extension sur un entier algébrique, c’est-à-dire si le polynôme minimal d'un nombre algébrique est à coefficients entiers, alors le discriminant de l'extension est égal à celui du polynôme minimal. La formule classique du discriminant pour les polynômes de degré deux donne b2 - 4.c si le polynôme est égal à X2 + b.X + c.
Le corps des entiers de Gauss
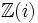 forme l'anneau des entiers de
forme l'anneau des entiers de 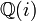 .
.Voir aussi
- Portail des mathématiques
Catégories : Entier quadratique | Carl Friedrich Gauss | Arithmétique modulaire
Wikimedia Foundation. 2010.