Théorème de Gauss-Wantzel

Théorème de Gauss-Wantzel
Page d'aide sur l'homonymie Pour les articles homonymes, voir Théorème de Gauss et Théorème de Wantzel.

En géométrie, le théorème de Gauss-Wantzel énonce une condition nécessaire et suffisante pour qu'un polygone régulier soit constructible à la règle et au compas.

Sommaire

Énoncés

Théorème de Gauss-Wantzel — Un polygone à n côtés est constructible si et seulement si n est le produit d'une puissance de 2 et d'un nombre fini de nombres premiers de Fermat distincts.

(Un nombre premier est dit de Fermat s'il est de la forme 2(2k)+1 pour un certain entier k.)

Ce théorème se déduit de :

Théorème de Wantzel — Un nombre complexe z est constructible si et seulement si l'extension Q(z)/Q peut se décomposer en une tour d'extensions quadratiques.

Histoire

Gauss avait pressenti cette condition nécessaire et suffisante mais n'avait démontré en 1796 qu'une implication : Si un polygone régulier possède n côtés et si n est une puissance de 2 ou est le produit d'une puissance de 2 et de k nombres de Fermat premiers différents alors ce polygone est constructible. C'est une analyse sur les polynômes cyclotomiques qui permet la démonstration de cette implication. Il avait laissé la réciproque sous forme d'une conjecture.

Pierre-Laurent Wantzel dans sa publication de 1837 démontre la réciproque grâce à sa condition nécessaire pour qu'un nombre soit constructible (théorème de Wantzel). C'est la notion de tour d'extensions quadratiques qui permet d'en apporter la preuve.

Démonstration

Le théorème de Gauss-Wantzel se déduit du théorème de Wantzel en traduisant sur n la condition pour que l'extension cyclotomique de Q par une racine primitive n-ième de l'unité se décompose en une tour d'extensions quadratiques.

Condition nécessaire pour que l'extension soit une tour d'extensions quadratiques.
Par définition d'une tour d'extensions quadratiques, une condition nécessaire est que la dimension de l'extension soit une puissance de deux. Étudions alors les entiers n tel que φ(n) soit une puissance de deux.

Remarquons tout d'abord que si n est égal à p.q avec p et q premiers entre eux alors nous avons l'égalité suivante φ(n) = φ(p).φ(q) (cf. l'article Indicatrice d'Euler). Considérons alors la décomposition de n en facteur premier (cf l'article Théorème fondamental de l'arithmétique).

n= \prod_{i=1}^k p_i^{\alpha_i}

L'indicatrice d'Euler d'une puissance d'un nombre premier pα est égale à (p - 1). pα -1. Il suffit donc de trouver une condition nécessaire et suffisante pour que le facteur (p - 1). pα -1 soit une puissance de deux et appliquer cette condition à chacun des facteurs de l'égalité précédente. Deux cas se présentent, soit p est égal à 2 et toute valeur de α est acceptable, soit p est un nombre premier de la forme 2k + 1 avec k un entier strictement positif et α est égal à 1. De plus, dans ce second cas, k est nécessairement une puissance de deux (voir Nombre de Fermat#Nombre de Fermat et primalité).

En conclusion n est de la forme suivante :

n=2^k \prod_iF_i~

Où les Fi sont des nombres premiers de Fermat distincts. Et la condition nécessaire est démontrée.

Condition suffisante pour que l'extension soit une tour d'extensions quadratiques.
Le polynôme cyclotomique est alors de degré φ(n) et est une puissance de 2. Notons 2k ce degré. Le groupe de Galois est alors le groupe cyclique de cardinal 2k.

Montrons que si l est un entier inférieur à k il existe un sous-groupe Gl du groupe cyclique de cardinal 2l et tel que si l est non nul alors Gl - 1 est inclus dans Gl. Définissons Gl comme le sous-groupe engendré par la classe de 2k-l. Par définition Gl - 1 est inclus dans Gl si l est non nul. De plus le cardinal de Gl est clairement égal à 2k-l.

On remarque ensuite que Gl-1 est un sous-groupe distingué de Gl car ce sont des groupes abéliens, donc tout sous-groupe est distingué. Ensuite le cardinal du groupe quotient de Gl par Gl - 1 est deux.

Le théorème fondamental de la théorie de Galois assure que si Kk- l est le sous-corps de l'extension qui laisse invariant tous les automorphismes de Gl (on a ici identifié le groupe de Galois et le groupe cyclique) alors si l est non nul Kl est une extension galoisienne de Kl - 1 de dimension deux donc quadratique, que K0 est égal au corps des nombres rationnels et que Kk est le corps de décomposition du polynôme cyclotomique.

Nous avons donc monté une tour d'extensions quadratiques du corps de décomposition et le théorème est démontré.

Cas du pentagone

Construction d'un pentagone
Article détaillé : Construction du pentagone régulier à la règle et au compas.

Le nombre 5 est de Fermat car il est premier et s'écrit 22 + 1. Ainsi la construction du pentagone régulier est réalisable. Un polygone régulier à 20 côtés est aussi constructible puisqu'il suffit de partir du pentagone régulier et de prendre (deux fois) la bissectrice de chaque angle. Et un polygone de 15 côtés aussi car 15 est le produit de deux nombres de Fermat. Euclide en avait d'ailleurs déjà établi une construction.

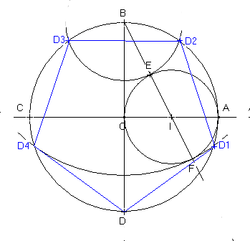
Si la théorie de Galois prend un aspect quelque peu abstrait, elle donne néanmoins une méthode de résolution effective de l'équation cyclotomique et en conséquence propose un mode de construction à la règle et au compas des polygones constructibles (cf l'article nombre constructible). Étudions le pentagone à cinq côtés.

A une similitude directe près du plan euclidien, les sommets du pentagone régulier sont exactement les cinq racines cinquièmes de l'unité. Par identification, ils sont, hormis 1, les racines du cinquième polynôme cyclotomique, soit donc :

\Phi_5(X) = X^4 + X^3 + X^2 + X + 1\,

.

Si l'équation correspondante est un polynôme du quatrième degré, elle est néanmoins résoluble avec une quantité de calcul faible. Le corps de décomposition, noté parfois F5, est (par oubli de structure) un espace vectoriel rationnel de dimension quatre. Son groupe de Galois G est le groupe cyclique d'ordre quatre. Il admet donc un générateur noté ici m et un sous-groupe non trivial H, contenant deux éléments, l'identité et m2. L'application qui à tout élément de l'extension associe son conjugué est un automorphisme qui laisse F5 stable, Q invariant et est d'ordre deux ; en conséquence m2 est précisément l'application conjuguée. L'objectif est donc de trouver le sous-corps de F5 de dimension deux sur Q, laissant ses éléments invariants par l'application conjuguée. Un jeu de permutation des racines permet alors de ramener la résolution de l'équation à trois équations simples du second degré.

Il est alors relativement simple d'obtenir une construction à la règle et au compas. Sur la figure illustrative, il est par exemple immédiat de remarquer que la longueur du segment BI est la moitié de la racine carrée de cinq, le radical de la première extension.

Calcul

Comme ci-dessus, z désigne la racine primitive cinquième privilégiée, à savoir exp(i.2.pi/5) et le générateur m du groupe de Galois est l'automorphisme sur Q de l'extension F5 uniquement défini par l'identité :

m(z) = z2
.

Déterminons les éléments de F5 laissés invariants par la conjugaison complexe m2. Or, m2(z)= z4 ; m2(z2)=z3 ; et enfin m2 est d'ordre deux. Donc u = z + z4 et son image v = m(u) = z2 + z3 sont clairement invariants par m2. De plus, leur somme u+v et leur produit u.v sont invariants par m et donc par le groupe de Galois ; on s'attend à ce qu'ils soient donc rationnels. La somme u+v est la somme des quatre racines cinquièmes et vaut donc -1 ; le produit est aussi égal à la somme des racines cinquièmes primitives, soit -1. On en déduit que u et v vérifie l'équation P[X] = 0 où :

P[X] = X^2 + X - 1 =0 \quad et \quad u = \frac{1}{2} (-1 + \sqrt{5}) \quad v = \frac{1}{2} (-1 - \sqrt{5})

Ces formules auraient pu être démontrées en remarquant que z4 est le conjugué de z. Il en est de même avec z2 et z3. En effet, on a :

z^4 + z^3 + z^2+ z+1 = \bar{z}+\bar{z}^2 + z^2 + z + 1 = (\bar{z} + z)^2 -2\bar{z}z + (\bar{z} + z)+ 1 = (\bar{z} + z)^2 + (\bar{z} + z)- 1

Avec :

-2\bar{z}z=-2z^5=-2

Et le carré du conjugué est égal au conjugué du carré de z.

L'ensemble des points fixes par m2, donc par H forment une extension intermédiaire de Q, notée habituellement F5H. Le polynôme Φ5[X] se factorise dans l'algèbre F5H[X] comme suit:

\Phi_5(X) = (X^2 -u.X + 1)(X^2 -v.X + 1)\,
u = \frac{1}{2} (-1 + \sqrt{5}) \quad et \quad v = \frac{1}{2} (-1 - \sqrt{5})

Et dans F5[X], le polynôme prend la forme:

\Phi_5(X) = (X - z)(X - \bar{z})(X - z^2)(X - \bar{z^2})\,
z = \frac{1}{4} (-1 + \sqrt{5})+ \frac{i}{4} \sqrt{10 + 2\sqrt{5}} \quad et \quad z^2 = \frac{1}{4} (-1 - \sqrt{5})+ \frac{i}{4} \sqrt{10 - 2\sqrt{5}}
.

Cas de l'heptadécagone

Figure à la règle et au compas: Heptadécagone, le polygone régulier de 17 côtés

Le nombre premier de Fermat suivant est dix-sept. Le polygone régulier à 17 côtés (heptadécagone régulier) est donc aussi constructible et Gauss en a donné une méthode de construction. Si la logique précédente s'applique avec le même succès, les calculs sont néanmoins plus complexes. Le polynôme à factoriser est maintenant de degré seize. En conséquence, ce cas n'a pas été traité avant une compréhension profonde des polynômes cyclotomiques.

La méthode de résolution proposée ici suit pas à pas la démarche de la théorie de Galois. Ce groupe est le groupe cyclique d'ordre seize. Il contient donc trois sous-groupes non triviaux. H1 est un sous-groupe à huit éléments, il contient les multiples de deux, H2 contient les multiples de quatre et H3 contient deux éléments le neutre et le multiple de huit, la même remarque que celle du paragraphe précédent montre que l'élément non neutre correspond à l'application conjuguée. Les sous-corps associés forment une chaîne d'extensions strictement emboitée tel que la dimension d'un corps est deux sur le corps précédent.

\mathbb{Q} \sub \mathbb{F}_{17}^{H_1} \sub \mathbb{F}_{17}^{H_2} \sub \mathbb{F}_{17}^{H_3} \sub \mathbb{F}_{17}\;

L'objectif est alors de trouver un générateur de chaque extension dans la précédente. La technique utilisé dite des périodes de Gauss est toujours la même. Explicitons la pour la première extension. Soit m2 le générateur du premier groupe (on a choisi m générateur du groupe de Galois), Considérons la somme des huit composées successives de z la première racine primitive, et la somme des huit autres racines:

u_1=\sum_{i=0}^7 m^{2i}(z)\quad et \quad u_2=\sum_{i=0}^7 m^{2i+1}(z)\;

Alors ces deux éléments sont invariant par le générateur m2. De plus, leur somme est égal à -1 car c'est la somme de toutes les racines primitives. Ils sont donc de la forme u1 = a + b.r et u2 = a - b.r où a et b sont des rationnels et r le radical générateur de l'extension, car nous sommes dans une extension quadratique. Leur produit est donc encore rationnel. On en déduit une équation du type P1[X] = 0 avec P1[X] un polynôme du deuxième degré.

Réitérer trois fois cette méthode donne alors la solution.

Calcul

Choisir m tel que m(z) = z2 n'est pas la solution car m est d'ordre huit. Il est donc plus judicieux de choisir m tel que m(z) = z3 m et m2 restreints aux racines sont donc deux permutations décrites par:

m= \left( \begin{matrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 3 & 6 & 9 & 12 & 15 & 1 & 4 & 7 \end{matrix} \quad \begin{matrix} 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 \\ 10 & 13 & 16 & 2 & 5 & 8 & 11 & 14 \end{matrix}\right)
m^2= \left( \begin{matrix} 1 & 9 & 13 & 15 & 16 & 8 & 4 & 2 \\ 9 & 13 & 15 & 16 & 8 & 4 & 2 & 1 \end{matrix} \right) \left( \begin{matrix} 3 & 10 & 5 & 11 & 14 & 7 & 12 & 6 \\ 10 & 5 & 11 & 14 & 7 & 12 & 6 & 3 \end{matrix}\right)

Alors u1 est la somme des racines de puissance: 1 ,9 ,13 ,15, 16, 8, 4, 2 et u2 les autres. Leur somme est égale à la somme des racines donc -1 et leur produit à quatre fois la somme des racines donc -4. On obtient:

P_1[X]=X^2+X -4=0 \quad et \quad u_1 = \frac{1}{2}(-1 + \sqrt{17}) \quad u_2 = \frac{1}{2}(-1 - \sqrt{17}))\,

Pour appliquer cette même logique une deuxième fois déterminons m4 :

m^4 = \begin{pmatrix} 1 & 13 & 16 & 4 \\ 13 & 16 & 4 & 1 \end{pmatrix} \begin{pmatrix} 9 & 15 & 8 & 2 \\ 15 & 8 & 2 & 9 \end{pmatrix} \begin{pmatrix} 3 & 5 & 14 & 12 \\ 5 & 14 & 12 & 3 \end{pmatrix} \begin{pmatrix} 10 & 11 & 7 & 6 \\ 11 & 7 & 6 & 10 \end{pmatrix}

Notons alors v1 la somme des racines d'exposant 1, 13, 16, 4 notons v2 la somme des racines d'exposant 2, 9, 15, 8 notons v3 la somme des racines d'exposant 3, 5, 14, 12 et v4 la somme des racines d'exposant 10, 11, 7, 6

P_2[X]=X^2-u_1X -1=0 \quad et \quad v_1 = \frac{1}{2}(u_1 + \sqrt{4+u_1^2}) \quad v_2 = \frac{1}{2}(u_1 - \sqrt{4+u_1^2})\,
P'_2[X]=X^2-u_2X -1=0 \quad et \quad v_3 = \frac{1}{2}(u_2 + \sqrt{4+u_2^2}) \quad v_4 = \frac{1}{2}(u_2 - \sqrt{4+u_2^2})\,

Le calcul effectif donne:

v_1 = \frac{1}{4}(-1 + \sqrt{17}+\sqrt{34-2\sqrt{17}}) \quad v_2 = \frac{1}{4}(-1 + \sqrt{17}-\sqrt{34-2\sqrt{17}})
v_3 = \frac{1}{4}(-1 - \sqrt{17}+\sqrt{34+2\sqrt{17}}) \quad v_4 = \frac{1}{4}(-1 - \sqrt{17}-\sqrt{34+2\sqrt{17}}) \,

L'étape suivante ne demande pas la détermination de m8 car il est établi que cette application est le conjugué, à une racine d'exposant i elle associe donc la racine d'exposant 17 - i. On choisit alors w1 comme la somme des racines d'exposant 1 et 16 et w2 comme la somme des racines d'exposant 13 et 4. On obtient:

P_3[X]=X^2-v_1X +v_3=0 \quad et \quad w_1 = \frac{1}{2}(v_1 + \sqrt{v_1^2-4v_3})\,
w_1 = \frac{1}{8}\left(-1 + \sqrt{17}+\sqrt{34-2\sqrt{17}} +\sqrt{68 +12\sqrt{17}-2\sqrt{34-2\sqrt{17}}-16\sqrt{34+2\sqrt{17}}+2\sqrt{578-34\sqrt{17}}}\right)\,

Le calcul de w1 suffit pour obtenir la racine primitive. On sait par construction que ce coefficient est égal à la somme de la première racine primitive et de son conjugué. On en déduit alors que:

z = \frac{1}{2}w_1+\frac{i}{2}\sqrt{1-w_1^2}\,

La construction à la règle et au compas est moins douloureuse qu'il n'y paraît, u1 a pour radical une longueur égal à l'hypoténuse d'un triangle de côté un et un quart. u2 a pour radical l'hypoténuse d'un triangle de côté 2 et u1. Seule l'étape suivante est un peu pénible. Un développement brutal laisserait en effet à penser à une construction plus délicate. Il donne.

\cos\left(\frac{2\pi}{17}\right) = \frac{1}{16}\left(-1 + \sqrt{17}+\sqrt{34-2\sqrt{17}} +\sqrt{68 +12\sqrt{17}-2\sqrt{34-2\sqrt{17}}-16\sqrt{34+2\sqrt{17}}+2\sqrt{578-34\sqrt{17}}}\right)\,

Résultats détaillés

Les cinq nombres de Fermat premiers connus sont :

F0 = 3, F1 = 5, F2 = 17, F3 = 257, et F4 = 65537
suite A019434 de l’OEIS.

Ainsi un polygone à n côtés est constructible à la règle et au compas si :

n = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, ...
suite A003401 de l’OEIS.

Tandis qu'il n'est pas constructible si :

n = 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25,...
suite A004169 de l’OEIS.

Par exemple, la construction (à la règle et au compas) de l'heptagone régulier n'est pas possible car le nombre premier 7 n'est pas de Fermat. L'entier 9 = 32 est le carré d'un nombre premier de Fermat, donc l'ennéagone régulier n'est pas constructible non plus.

Application


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Gauss-Wantzel de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Theoreme de Gauss-Wantzel — Théorème de Gauss Wantzel Pour les articles homonymes, voir Théorème de Gauss. En géométrie, le théorème de Gauss Wantzel précise la condition nécessaire et suffisante pour qu un polygone régulier soit constructible à la règle et au compas.… …   Wikipédia en Français

  • Théorème de gauss-wantzel — Pour les articles homonymes, voir Théorème de Gauss. En géométrie, le théorème de Gauss Wantzel précise la condition nécessaire et suffisante pour qu un polygone régulier soit constructible à la règle et au compas. Théorème de Gauss Wantzel  …   Wikipédia en Français

  • Theoreme de gauss — Théorème de Gauss Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Plusieurs lemmes ou théorèmes portent le nom de Gauss, en référence au mathématicien Carl Friedrich Gauss : Un lemme de Gauss… …   Wikipédia en Français

  • Théorème de gauss — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Plusieurs lemmes ou théorèmes portent le nom de Gauss, en référence au mathématicien Carl Friedrich Gauss : Un lemme de Gauss généralisant le lemme d …   Wikipédia en Français

  • Théorème de Gauss — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Plusieurs lemmes ou théorèmes portent le nom de Gauss, en référence au mathématicien Carl Friedrich Gauss. Lemmes : un lemme de Gauss en arithmétique …   Wikipédia en Français

  • Theoreme d'Abel (algebre) — Théorème d Abel (algèbre) Pour les articles homonymes, voir Théorème d Abel. Niels Henrik Abel (1802 …   Wikipédia en Français

  • Théorème d'Abel-Ruffini — Théorème d Abel (algèbre) Pour les articles homonymes, voir Théorème d Abel. Niels Henrik Abel (1802 …   Wikipédia en Français

  • Théorème d'Abel (Algèbre) — Pour les articles homonymes, voir Théorème d Abel. Niels Henrik Abel (1802 …   Wikipédia en Français

  • Théorème d'abel (algèbre) — Pour les articles homonymes, voir Théorème d Abel. Niels Henrik Abel (1802 …   Wikipédia en Français

  • Théorème de Wantzel — Le théorème de Wantzel, énoncé par Pierre Laurent Wantzel en 1837[1], précise les conditions nécessaires et suffisantes pour qu un nombre soit constructible. Il peut s énoncer de la manière suivante Le réel a est constructible si et seulement s… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”