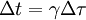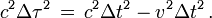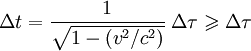Ralentissement des horloges

Ralentissement des horloges

Dilatation du temps

La dilatation du temps est un effet de relativité restreinte selon lequel une horloge animée d'une certaine vitesse par rapport à un référentiel que nous qualifierons de fixe sera vue battre le temps à un rythme plus lent quand on le rapporte à celui des horloges de ce référentiel. Pour dire les choses (trop) rapidement : une horloge en mouvement retarde.

Ce phénomène de ralentissement des horloges s'étend, en relativité générale, aux horloges proches d'un corps massif, qui vont ralentir par rapport à celles qui en sont plus éloignées.

Sommaire

En relativité restreinte

Survol

Pensons à une horloge embarquée dans une fusée et lue par des observateurs fixes (disons terrestres, au repos par rapport à la Terre) répartis le long de sa trajectoire au moment où elle passe devant chacun d'eux. La formule donnant la dilatation du temps en relativité restreinte est :

\Delta t = \gamma \Delta \tau \!

où

Δτ est l'intervalle de temps mesuré avec l'horloge « en mouvement » de la fusée,
Δt est l'intervalle de temps mesuré par les observateurs terrestres,
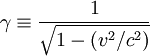\gamma \equiv \frac{1}{\sqrt{1 - (v^2/c^2)}} est le facteur de Lorentz,
v est la vitesse de la fusée par rapport à la Terre et c la vitesse de la lumière.

Suivie par des horloges réparties sur son chemin, l'horloge en mouvement semble avoir subi une augmentation de la durée de son cycle.

Cet effet est négligeable pour de faibles vitesses et c'est la raison pour laquelle la correction n'intervient pas dans la vie courante et que le phénomène n'est pas perceptible d'ordinaire. En revanche dès qu'un objet atteint une vitesse de l'ordre du 1/10 de celle de la lumière, ou lorsque la précision demandée est importante, comme dans le cas d'un GPS, l'effet relativiste est notable et peut même devenir colossal si v se rapproche tout près de la valeur c.

La dilatation du temps par le facteur de Lorentz a été prédite par Joseph Larmor (1897), au moins pour les électrons en orbite autour d'un noyau. Il a écrit

« Les électrons individuels décrivent les parties correspondantes de leurs orbites en un temps plus court que le système [au repos] dans le rapport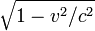 \sqrt{1 - v^2/c^2} . »

La grandeur de la dilatation du temps correspondant au facteur Lorentz a été expérimentalement confirmée.

Calcul

Considérons deux événements, par exemple l'émission de deux éclairs, séparés par l'intervalle Δτ  mesuré dans la fusée. Les éclairs sont émis alors que la fusée passe devant deux observateurs terrestres lisant l'heure sur leur montre et constatant que leurs lectures diffèrent du temps Δt . Comme la fusée se déplace à la vitesse v par rapport à la Terre, la distance entre ces deux observateurs terrestres concernés est de v Δt. Les deux mêmes événements « éclairs » étant séparés par l'intervalle d'espace-temps (Δx =vΔt, Δt ) dans le repère terrestre et (0, Δτ ) dans le repère de la fusée, la relativité restreinte affirme que le carré de l'intervalle d'espace-temps entre les deux événements est le même dans les deux repères et que de ce fait l'égalité suivante est respectée :

c^2 \Delta\tau^2 \,=\, c^2 \Delta{t}^2 - v^2 \Delta{t}^2\,.

On en déduit aussitôt que :

\Delta{t} = \frac{1}{\sqrt{1 - (v^2/c^2)}}\;\Delta\tau \geqslant \Delta\tau

comme il fallait le démontrer.

voir aussi Temps propre

Vérifications expérimentales

  • On a observé que les particules instables se désintègrent plus lentement du point de vue de l'observateur lorsqu'elles se meuvent à grande vitesse par rapport à celui-ci, notamment dans les accélérateurs de particules.
  • Cet effet est également observé pour les muons atmosphériques produits par la collision des rayons cosmiques (particules très énergétiques en provenance de l'espace cosmique) et les molécules de l'atmosphère. Ces muons, animés d'une vitesse proche de celle de la lumière, atteignent le sol où ils sont observés et ce malgré leur courte durée de vie propre, la dilatation du temps leur donnant le temps nécessaire pour atteindre les détecteurs.
  • Un autre cas observé de dilatation temporelle est le décalage entre horloges atomiques au sol et en vol ; mais il se complique dans ce dernier cas de considérations gravitationnelles de sorte que le cadre de la relativité restreinte est insuffisant et qu'on doit considérer les effets de Relativité générale. Incidemment l'expérience réelle d'horloges atomiques embarquées en avion est une version réalisable, et souvent réalisée, de l'expérience des jumeaux, laquelle exploite l'effet de ralentissement des horloges en mouvement.
  • Signalons également que l'on observe aussi une dilatation du temps lorsqu'on mesure la durée de l'évolution de la luminosité des supernovae lointaines, mais que ce dernier effet est du à l'expansion de l'univers.

Dilatation du temps et navigation imaginaire dans l'espace

Article détaillé : Paradoxe des jumeaux.

Avec la dilatation du temps, il serait mathématiquement possible (mais irréalisable en pratique !) qu'une horloge allant à une vitesse quasiment égale à celle de la lumière voyage dans le futur en vieillissant très peu. Ceci serait possible puisque l'horloge (mais aussi un être humain) qui se déplace vieillira moins vite que l'horloge stationnaire. Par exemple, à quelque 12 ans de voyage dans une fusée soumise à une accélération de 1 g correspondraient 100 000 ans sur Terre, et cette durée permettrait de traverser notre Galaxie (toujours en théorie !).

En relativité générale

Description du phénomène

En relativité générale, la courbure de l'espace-temps (c'est-à-dire la gravitation) ralentit le temps mesuré dans un champ de gravitation par rapport à celui mesuré hors champ de gravitation : si deux horloges sont identiques et que l'une a fait un séjour dans un champ de gravitation, alors elle retarde par rapport à l'autre, et ce d'autant plus que la gravitation a été forte.

Métrique de Schwarzschild

On sait que la métrique est ds2 = gijdxidxj. Dans le cas d'une masse à symétrie sphérique, on peut utiliser la métrique de Schwarzschild

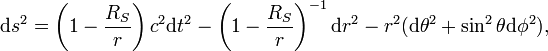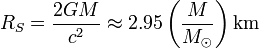\mathrm ds^2=\left(1-\frac{R_S}{r}\right)c^2\mathrm dt^2 -\left(1-\frac{R_S}{r}\right)^{-1}\mathrm dr^2-r^2(\mathrm d \theta^2 +\sin^2 \theta \mathrm d \phi^2), avec R_S = \frac{2GM}{c^2}\approx 2.95\left(\frac{M}{M_\odot}\right) \mathrm{km} le rayon de Schwarzschild de la masse sphérique, strictement inférieur au rayon r.

On en déduit 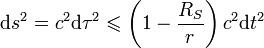\mathrm ds^2 =c^2\mathrm d\tau^2 \leqslant \left(1-\frac{R_S}{r}\right)c^2\mathrm dt^2. Ainsi 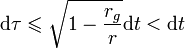\mathrm d\tau \leqslant \sqrt{1-\frac{r_g}{r}}\mathrm dt < \mathrm dt où dτ est l'élément infinitésimal de temps propre du corps, et dt est celui du temps mesuré dans le référentiel de l'observateur, par hypothèse non soumis à la gravitation (sinon les formules sont différentes).

On peut dire que par la gravitation le temps propre est ralenti par rapport au temps du référentiel (qui est par hypothèse mesuré hors d'influence de la masse), ou que le temps impropre est dilaté par rapport au temps propre du corps influencé par la gravitation.

Cas d'un trou noir

Dans le cas d'un trou noir, ici réduit à ses caractéristiques liées à la métrique, une horloge peut s'approcher du rayon de Schwarzschild 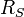\ R_S du corps massif. En la supposant quasi-immobile dans le référentiel, elle marque son temps propre dτ = ds / c, et le temps dt observé très loin du trou noir (à l'infini, pour faire court) est \mathrm dt = \frac{\mathrm d\tau }{\sqrt{1-\frac{R_S}{r}}} \xrightarrow[r \to R_S]{} \infty. Ce qui signifie que au fur et à mesure que l'horloge s'approche du rayon de Schwarzschild, le temps de l'horloge parait mettre un temps infini pour s'écouler aux yeux de l'observateur, et semble même s'arrêter à ses yeux, mais l'horloge ne s'arrête pas pour elle-même.

Résultats expérimentaux

En 1977, une expérience embarquant des horloges atomiques dans une fusée a confirmé les prévisions théoriques avec une précision de 0,01%.[1] En 1959, Robert Vivian Pound et Glen Rebka ont pu vérifier expérimentalement que la différence d'altitude de 22,6 mètres d'une tour de l'Université de Harvard donnait une différence de fréquence de la lumière conforme aux prévisions de la relativité générale.[1],[2]

Notes

  1. ↑ a  et b  Jean-Claude Boudenot, chapitre VI p145 à p147 de Électromagnétisme et gravitation relativiste, édité chez ellipse en 1989, ISBN 2-7298-8936-1.
  2. ↑ R. V. Pound, « Gravitational Red-Shift in Nuclear Resonance », dans Physical Review Letters, vol. 3, no 9, 1e November 1959, p. 439–441 [texte intégral lien DOI (pages consultées le 2006-09-23)] 

Liens externes

Voir aussi

Bibliographie

  • Portail de la physique Portail de la physique
Ce document provient de « Dilatation du temps ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Ralentissement des horloges de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Ralentissement du temps — Dilatation du temps La dilatation du temps est un effet de relativité restreinte selon lequel une horloge animée d une certaine vitesse par rapport à un référentiel que nous qualifierons de fixe sera vue battre le temps à un rythme plus lent… …   Wikipédia en Français

  • Paradoxe des jumeaux — En physique, le paradoxe des jumeaux (parfois appelé paradoxe de Langevin) est une expérience de pensée qui semble montrer que la relativité restreinte est contradictoire. En fait, le paradoxe n a jamais été véritablement considéré comme une… …   Wikipédia en Français

  • Jumeaux de langevin — Paradoxe des jumeaux Le paradoxe des jumeaux est une expérience de pensée qui semble montrer que la relativité restreinte est contradictoire. Dans les ouvrages d enseignement, il est mis en avant pour ses vertus pédagogiques et peut être l… …   Wikipédia en Français

  • Paradoxe de Langevin — Paradoxe des jumeaux Le paradoxe des jumeaux est une expérience de pensée qui semble montrer que la relativité restreinte est contradictoire. Dans les ouvrages d enseignement, il est mis en avant pour ses vertus pédagogiques et peut être l… …   Wikipédia en Français

  • Voyageur de Langevin — Paradoxe des jumeaux Le paradoxe des jumeaux est une expérience de pensée qui semble montrer que la relativité restreinte est contradictoire. Dans les ouvrages d enseignement, il est mis en avant pour ses vertus pédagogiques et peut être l… …   Wikipédia en Français

  • Relativité restreinte — Pour les articles homonymes, voir relativité. La relativité restreinte est la théorie formelle élaborée par Albert Einstein en 1905 en vue de tirer toutes les conséquences physiques de la relativité galiléenne et du principe que la vitesse de la… …   Wikipédia en Français

  • Dilatation du temps — La dilatation du temps est un effet de relativité restreinte selon lequel une horloge animée d une certaine vitesse par rapport à un référentiel que nous qualifierons de fixe sera vue battre le temps à un rythme plus lent quand on le rapporte à… …   Wikipédia en Français

  • Dilatation Du Temps — La dilatation du temps est un effet de relativité restreinte selon lequel une horloge animée d une certaine vitesse par rapport à un référentiel que nous qualifierons de fixe sera vue battre le temps à un rythme plus lent quand on le rapporte à… …   Wikipédia en Français

  • Geometrie de l'espace-temps dans les reperes tournants — Géométrie de l espace temps dans les repères tournants Nous allons aborder dans cet article la géométrie de l espace temps dans un repère en rotation. Plus spécifiquement nous considérerons un disque en rotation et nous allons voir quelle forme… …   Wikipédia en Français

  • Géométrie De L'espace-Temps Dans Les Repères Tournants — Nous allons aborder dans cet article la géométrie de l espace temps dans un repère en rotation. Plus spécifiquement nous considérerons un disque en rotation et nous allons voir quelle forme prend la géométrie de l espace temps pour un observateur …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”