Symétrie sphérique
- Symétrie sphérique
-
Symétrie de rotation
Definition générale
En physique, la symétrie de rotation, ou invariance par rotation, ou encore isotropie, est la propriété d'une théorie, ou d'un système physique qui n'est pas transformé par une rotation. En mathématiques cette propriété s'applique à un objet géométrique mais également à d'autre objets comme par exemple un opérateur (par exemple le laplacien de l'espace 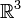 est invariant par rotation).
est invariant par rotation).
Exemples d'objets[1]
Très symétriques
- La sphère, sur ce point de vue, est parfaite, (c'est d'ailleurs l'objet le plus symétrique) : une rotation autour de n'importe quel axe qui passe par le centre, de n'importe quel angle orienté aboutira au même résultat, la sphère reste mathématiquement, inchangée.
- La cube est nettement moins symétrique : il ne le sera que par une rotation de + ou - 90° sur un des axes qui passe par son centre.
Moins symétriques
- Le tétraèdre n'est pas très symétrique : une rotation sur l'axe passant par un sommet et le centre de la face opposée, d'un angle orienté de 120° aboutit au même résultat.
Notes
- ↑ il existe, bien entendu une infinité d'objet qui sont symétriques par rotation, ici ne sont repris que les plus fréquents
Liens internes
 Portail de la physique
Portail de la physique Portail de la géométrie
Portail de la géométrie
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Symétrie sphérique de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
symétrie sphérique — sferinė simetrija statusas T sritis fizika atitikmenys: angl. spherical symmetry vok. Kugelsymmetrie, f rus. сферическая симметрия, f pranc. symétrie sphérique, f … Fizikos terminų žodynas
onde de symétrie sphérique — sferiškai simetrinė banga statusas T sritis fizika atitikmenys: angl. spherically symmetric wave vok. kugelsymmetrische Welle, f; sphärosymmetrische Welle, f rus. сферически симметричная волна, f pranc. onde de symétrie sphérique, f … Fizikos terminų žodynas
Symétrie des figures d'équilibre — Théorie des figures d équilibre La théorie des figures d équilibre considérée ici résulte de nombreuses études traitant du problème de la forme d équilibre de la Terre, en supposant que celle ci soit causée par la seule force de pesanteur, à l… … Wikipédia en Français
symétrie — [ simetri ] n. f. • 1530 archit.; lat. symmetria, mot gr. « juste proportion », de sun « avec » et metron « mesure » I ♦ 1 ♦ Vx Juste proportion, accord des parties d un bâtiment entre elles et avec l ensemble, qui concourt à la beauté de l… … Encyclopédie Universelle
Groupe De Symétrie — Un tétraèdre peut être placé dans 12 positions distinctes par une seule rotation. Celles ci sont illustrées ci dessus dans le format d un graphe de cycle, avec des rotations à 180° par rapport à une arête (flèches bleues) et à 120° par rapport à… … Wikipédia en Français
Groupe de symetrie — Groupe de symétrie Un tétraèdre peut être placé dans 12 positions distinctes par une seule rotation. Celles ci sont illustrées ci dessus dans le format d un graphe de cycle, avec des rotations à 180° par rapport à une arête (flèches bleues) et à… … Wikipédia en Français
Groupe de symétrie — Un tétraèdre régulier peut être placé dans 12 positions distinctes par une seule rotation. Celles ci sont illustrées ci dessus dans le format d un graphe de cycles avec des rotations à 180° par rapport à une arête (flèches bleues) et à 120° par… … Wikipédia en Français
Harmonique Sphérique — En mathématiques, les harmoniques sphériques sont des fonctions harmoniques particulières. À titre de rappel, une fonction est dite harmonique lorsque son laplacien est nul. Les harmoniques sphériques sont particulièrement utiles pour résoudre… … Wikipédia en Français
Harmonique spherique — Harmonique sphérique En mathématiques, les harmoniques sphériques sont des fonctions harmoniques particulières. À titre de rappel, une fonction est dite harmonique lorsque son laplacien est nul. Les harmoniques sphériques sont particulièrement… … Wikipédia en Français
Harmonique sphérique — En mathématiques, les harmoniques sphériques sont des fonctions harmoniques particulières. À titre de rappel, une fonction est dite harmonique lorsque son laplacien est nul. Les harmoniques sphériques sont particulièrement utiles pour résoudre… … Wikipédia en Français
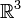 est invariant par rotation).
est invariant par rotation).