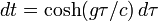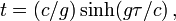- Paradoxe de Langevin
-
Paradoxe des jumeaux
Le paradoxe des jumeaux est une expérience de pensée qui semble montrer que la relativité restreinte est contradictoire. Dans les ouvrages d'enseignement, il est mis en avant pour ses vertus pédagogiques et peut être l'occasion de se livrer à des calculs précis sur le ralentissement des horloges.[1]
- Le paradoxe
Des frères jumeaux sont nés sur terre. L'un fait un voyage dans l'espace en fusée à une vitesse proche de celle de la lumière. D'après le phénomène de ralentissement des horloges en mouvement de la relativité restreinte, celui qui est resté sur terre voit que celui qui voyage vieillit moins vite que lui. Mais celui qui voyage voit son frère s'éloigner à grande vitesse de lui et, d'après le même phénomène, voit le frère resté sur terre vieillir moins vite que lui. Ainsi d'après ce raisonnement utilisant la relativité restreinte, chacun voit l'autre vieillir moins vite : c'est absurde car au retour du voyageur, ils ne peuvent être tous les deux plus vieux que l'autre !
- Sa résolution
En réalité, les situations des jumeaux ne sont pas symétriques : le sédentaire coïncide avec un seul repère galiléen (celui de la Terre) pendant toute la durée du voyage, tandis que le voyageur effectue un demi-tour et coïncide ainsi avec au moins deux repères galiléens successifs. Cette différence fait que la relativité restreinte s'applique différemment à l'un et à l'autre, notamment le « ralentissement des horloges en mouvement » n'est vrai sur l'ensemble du voyage qu'aux yeux du frère restant dans un seul référentiel inertiel. Au final, c'est celui qui a fait l'aller-retour dans la fusée qui a vieilli moins vite que celui qui est resté sur terre.
Histoire
Au sujet de la dilatation du temps prédite par la relativité restreinte, Albert Einstein indique en 1911
«Si nous placions un organisme vivant dans une boîte … on pourrait s'arranger pour que cet organisme, après un temps de vol aussi long que voulu, puisse retourner à son endroit d'origine, à peine altéré, tandis que les organismes correspondants, qui sont restés dans leur position initiale auraient depuis longtemps cédé la place à de nouvelles générations. Car pour l'organisme en mouvement, la grande durée du voyage était un court instant, à condition que le mouvement ait été effectué quasiment à la vitesse de la lumière.[2]
»La même année, Paul Langevin développe cette expérience de pensée sous une forme qui passe à la postérité :[3] « le boulet de Jules-Verne Langevin » où il relate de manière réaliste le déroulement de la vie de deux frères jumeaux dont l'un voyage à une vitesse proche de la lumière et l'autre reste sur Terre. Cet exposé, lors de la Conférence au Congrès de philosophie de Bologne en 1911, permet de populariser la notion du temps en relativité et d'illustrer la révolution philosophique qu'elle apporte[4].
Le nom de « paradoxe » a été donné à l'expérience de pensée par ceux qui y voyaient une incohérence de la théorie : ils arguaient en effet de la symétrie du problème en invoquant la relativité du mouvement et concluaient que, quel que soit le jumeau choisi, celui-ci devait mesurer une durée plus courte que son frère et se retrouver plus jeune lors des retrouvailles, d'où une contradiction. Ce raisonnement est toutefois erroné car en vérité les deux jumeaux ne sont pas interchangeables, comme l'explique le présent article.
Le voyageur de Langevin
Imaginons deux frères jumeaux, appelons-les Pantoufle et Bougeotte. Pantoufle reste sur Terre tandis que son frère entame un voyage dans l'espace à très grande vitesse, proche de celle de la lumière (ce qui est par ailleurs de nos jours impossible à réaliser concrètement). Lorsque Bougeotte revient sur Terre, il découvre son frère Pantoufle plus âgé que lui. Ce fait illustre le phénomène de dilatation du temps prévu par la relativité restreinte tenant en ce que pour les observateurs terrestres une horloge embarquée semble tourner plus lentement que les leurs. Pour Pantoufle, Bougeotte a donc moins vieilli que lui-même.
Comment expliquer ce qui se passe pendant le trajet ? Considérons un ensemble d'observateurs au repos par rapport à la Terre (ou, si on préfère, se déplaçant à la même vitesse et restant de ce fait à une distance invariable les uns des autres) et disposés le long de la trajectoire de la fusée de Bougeotte, jusqu'à la planète lointaine que ce dernier va rejoindre. Nous les appellerons les « observateurs terrestres ». Ces observateurs auront au préalable synchronisé leurs horloges[5] et utilisent donc tous la même heure. Le phénomène que prévoit la relativité restreinte est que chaque observateur terrestre constate tour à tour, lorsque la fusée passe en face de lui, que l'heure de la fusée retarde par rapport à la sienne (qui représente l'heure terrestre de Pantoufle). Lorsque Bougeotte arrivera sur sa planète lointaine il sera en retard sur cette heure terrestre, comme il pourra le constater sur l'horloge donnant sur cette planète l'heure de Pantoufle.
Si Bougeotte fait maintenant demi-tour pour revenir sur Terre, il doublera son retard de l'aller et rejoindra finalement son frère Pantoufle en se retrouvant au final plus jeune que ce dernier.
Maintenant, puisqu'en relativité restreinte les vitesses sont réputées relatives, peut-on considérer que c'est la fusée qui est au repos et la Terre qui se déplace ? Les effets de réciprocité entre deux systèmes de référence inertiels, qui sont le propre de la théorie de la relativité, peuvent-ils inverser les conclusions relatives au vieillissement moindre du jumeau voyageur ? Comme aucun des jumeaux ne peut être à la fois le plus âgé et le moins âgé, n'y aurait-il pas là un « paradoxe » au sens de contradiction logique ? Non, en réalité il n'y a pas de paradoxe car il n'y a pas réciprocité entre Pantoufle et Bougeotte. Le premier conserve par rapport à tout référentiel galiléen un mouvement rectiligne et uniforme. En particulier Pantoufle est au repos dans le système constitué par tous les observateurs terrestres. Au contraire le voyageur Bougeotte possède successivement (éventuellement en dehors des phases d'accélération) deux mouvements simples (uniformes, à vitesse constante) distincts puisque de sens contraires. Le raisonnement détaillé est donné dans tout ce qui suit.
La question de savoir si le mouvement de Bougeotte est uniforme ou non, c'est-à-dire si la fusée est accélérée ou au contraire animée d'un mouvement uniforme, ne change rien au raisonnement. La relativité restreinte peut traiter les deux cas. Pour preuve nous donnerons plus loin les formules relativistes concernant une fusée soumise à une accélération constante.
Notion de repère
Pour montrer l'impossibilité d'échanger le référentiel de Pantoufle contre celui de Bougeotte, précisons la notion de repère. On parle souvent du repère de Bougeotte et du repère de Pantoufle comme si un repère se limitait à un seul lieu. Or ce point de vue est inexact. En relativité restreinte, un repère (ou référentiel, ou système de coordonnées) doit s'imaginer comme un ensemble de fusées voyageant en formation les unes à la suite des autres loin de toute masse gravitante (donc dans un espace « plat »), à la même vitesse et sans que leurs moteurs exercent d'accélération (ou freinage). Ces fusées contiennent une horloge (visible de l'extérieur), chacune étant synchronisée[5] avec les autres, et portent le signe de leur position dans le convoi spatial (un numéro d'ordre ou la distance à une fusée origine).
Quand nous parlons de repère terrestre il faut penser à un ensemble d'observateurs possédant des montres marquant la même heure et situés le long du trajet que suivra la fusée de Bougeotte. Quand nous parlons du repère de la fusée, nous devons imaginer un ensemble de fusées accompagnant celle de Bougeotte. Un repère ce n'est pas une fusée, c'est un train de fusées[6].
Cette vision des choses permet de mieux faire apparaître la dissymétrie entre les jumeaux (et également d'imaginer plus loin une expérience évoquant la symétrie de deux repères se croisant l'un l'autre). En effet, pour faire le suivi de la fusée de Bougeotte il est nécessaire de faire appel à deux trains de fusées, un pour l'aller, un pour le retour. Si deux convois sont nécessaires c'est qu'il n'est pas question de faire faire un demi-tour aux fusées volant en formation car cela violerait la nature du repère galiléen, pour lequel il est « interdit » d'allumer des moteurs. Pour suivre le mouvement de Pantoufle un seul train de fusées suffit.
Temps propre
Alors que la physique de Newton était basée sur le suivi de points repérés dans un espace absolu en fonction d'un temps absolu, la relativité restreinte assure le suivi d’événements. Un événement est caractérisé par une position (où il se passe) et un temps (à quel moment il se passe). La valeur des coordonnées dépend du système (repère) dans lequel on effectue les mesures. Le propre de la théorie de la relativité restreinte est d'établir le lien entre les différents systèmes de coordonnées.
On parle à juste titre de réciprocité entre repères, les vitesses n'ayant rien d'absolu. Cependant il existe un très grand nombre de situations où l'on examine le mouvement d'une particule, ou d'une fusée. Dans ce cas, il est évident qu'un repère joue un rôle bien particulier, celui dans lequel la particule (la fusée) est au repos. De ce point de vue il faut être vigilant avant d'affirmer que tous les repères sont équivalents.
Plaçons nous dans la fusée de Bougeotte et lisons le temps τ qu'indique l'horloge interne. Par rapport à elle-même il est évident que la fusée est au repos. Elle est également au repos par rapport aux autres fusées qui l'accompagnent et qui constituent avec elle l'ensemble du système de référence. En revanche pour les observateurs terrestres répartis le long du trajet, le temps mesuré sera le temps terrestre, que nous noterons t, et la position sera notée x (c'est la coordonnée de l'observateur devant lequel passe la fusée à l'instant temps t).
Considérons alors deux événements successifs, par exemple le passage de la fusée devant l'observateur terrestre x = 0 au temps t = 0 et le passage devant l'observateur x au temps t. Dans la fusée les temps correspondant à ces événements sont 0 et τ. Dans ces conditions, la relativité restreinte énonce le résultat fondamental suivant :
La quantité
ne dépend pas du repère dans lequel elle est évaluée.
Le temps τ est appelé le temps propre de la fusée.
Cette formule montre immédiatement qu'une durée propre est toujours plus petite que la même durée évaluée dans un autre repère. Ce résultat est capital et constitue la façon correcte d'énoncer l'effet de relativité restreinte sur la mesure des temps. Le temps mesuré dans la fusée pour des événements se produisant dans la fusée sera plus petit que celui mesuré sur Terre. Les horloges de la fusée semblent ralentir. Du point de vue des Terriens le temps de la fusée est comme dilaté.
Dilatation des durées
Les temps mesurés sur Terre seront donc toujours plus longs que ceux mesurés dans la fusée. La formule précédente permet de calculer immédiatement le rapport entre temps propre de la fusée et temps dans le repère extérieur terrestre. La fusée se déplaçant à la vitesse v parcourt la distance x = v t pendant le temps t et par conséquent en écrivant
on aboutit immédiatement à la célèbre formule
ou
Le « paradoxe des jumeaux » utilise cette augmentation des durées prévue par la relativité restreinte lorsqu'on passe du temps propre intérieur d'un mobile donné (fusée, particule) à un temps extérieur (la Terre, le laboratoire).
Cette dilatation des durées s'est toujours vérifiée expérimentalement.
Réciprocité
Il faut prendre des précautions pour établir une réciprocité entre la mesure du temps dans la fusée et la mesure du temps sur Terre. En effet nous avons fait jouer un rôle particulier au repère propre de l'objet suivi, en ce cas la fusée. Si donc nous voulons symétriser l'expérience, il faut nous placer sur Terre et, de la même façon que nous repérions la trajectoire de la fusée par rapport à un ensemble d'observateurs terrestres, il faut repérer le mouvement de notre Terre par rapport à un « train de fusées », chacune étant dotée de son horloge et de sa balise de position.
Pour visualiser une situation symétrique on pourrait imaginer la situation suivante en considérant deux convois de fusées, chacun constituant un repère inertiel, se déplaçant parallèlement l'un à l'autre. D'un côté les Terriens, de l'autre les Virginides. Tous les Terriens sont au repos les uns par rapport aux autres, leurs distances mutuelles sont invariables et leurs horloges sont synchronisées[5]. Il en est de même pour les Virginides. Le phénomène de dilatation du temps (ou de ralentissement des horloges) consiste en ce que chaque Virginide dans sa propre fusée voyant défiler devant lui des Terriens constaterait que l'horloge de ces derniers vue à travers le hublot avance au fur et à mesure que le temps s'écoule (ce Virginide dans sa fusée joue le rôle du Bougeotte de l'histoire, vieillit moins vite que dans un repère extérieur et voit donc les « autres » vieillir plus vite). Mais un Terrien donné voyant défiler devant lui des Virginides constaterait de la même façon que les horloges de ces derniers battent plus vite que la sienne. Au bout par exemple de 60 minutes de son temps, les horloges auraient avancé de 75 minutes.
- Pour chaque astronaute dans sa fusée se fiant à son temps propre, le temps s'écoule plus vite dans le repère défilant d'en face.
Quoiqu'un peu lourd le tableau ci-dessous a pour but de lever toute mésintelligence du phénomène de ralentissement des horloges. Il rassemble le relevé des observations consignées par les différents partenaires de l'expérience ici imaginée. La première colonne indique l'événement : la fusée V0 de Virginide passe devant telle ou telle fusée de Terrien. Les colonnes suivantes indiquent les coordonnées de cet événement dans l'un et dans l'autre repère. Il est clair que pour V0 les horloges des Terriens tournent plus vite que la sienne alors que pour les Terriens l'horloge de la fusée V0 ralentit par rapport aux leurs. Le tableau serait en tous points symétrique si maintenant une fusée (au singulier) de Terrien observait le passage des fusées (au pluriel) des Virginides .
Observation par les Terriens du passage de la fusée V0 des Virginides
ou
Observation du défilement des fusées des Terriens depuis la fusée V0Événement : node la fusée de Terrien devant laquelle passe la fusée V0 Heure mesurée par les Terriens
(en minutes)Heure mesurée par la fusée V0
(en minutes)Distance à la fusée de Terrien no0 (unité arbitraire) 0 0 0 0 1 10 8 60 2 20 16 120 3 30 24 180 5 50 40 300 10 100 80 600 Pour revenir à une image qui se rapproche de celle des jumeaux, supposons que tous les Terriens aient le même âge entre eux et que tous les Virginides aient aussi le même âge entre eux. Supposons alors qu'un astronaute A voie dans l'autre convoi à un moment donné (pris pour origine) une personne B du même âge que lui. Dans les années qui suivront, A verra les occupants des fusées d'en face vieillir plus vite que lui. Et on ne sera pas étonné d'apprendre, réciprocité oblige, que l'astronaute B fera en ce qui le concerne la même constatation : ceux qui défilent devant lui vieillissent plus vite que lui. Comme il se doit, les choses sont symétriques. Mais dans cette expérience, A et B ne se voient pas vieillir l'un l'autre puisqu'ils ne se rencontrent plus par la suite. Il est donc impossible à ces deux personnes de comparer leur destin.
C'est bien la particularité du paradoxe de Langevin de faire se retrouver les deux astronautes A et B, qui autrement ne se seraient vus qu'une fois. Et ces retrouvailles sont possibles grâce au fameux demi-tour de l'un des deux.
La première leçon à tirer de cette discussion est la suivante. Lorsqu'on dit bien trop vite qu'il y a dilatation du temps (ou ralentissement des horloges) dans un repère en mouvement (comme celui d'une fusée par rapport à la Terre), il faut préciser de quoi on parle… Il est beaucoup plus juste de parler de temps propre dans un repère donné, de se rappeler que la définition de ce temps propre suppose que l'on s'intéresse à des processus se produisant en un lieu donné et que, cela étant, la durée propre entre deux événements est toujours plus petite que la durée entre ces deux mêmes événements calculée dans d'autres repères.
La seconde leçon est que la vitesse entre deux repères est bien relative : il est impossible de distinguer entre un repère qui serait au repos absolu et un repère qui serait en mouvement absolu, le ralentissement des horloges ne s'appliquant qu'à l'un des deux. Le ralentissement des horloges est en lui-même parfaitement symétrique. Si on prend deux repères en mouvement l'un par rapport à l'autre, une horloge de l'un sera toujours vue comme ralentie lorsque son allure est mesurée par un ensemble d'observateurs appartenant à l'autre. Incontestablement il apparaît « paradoxal » que, quel que soit le côté choisi, Terrien ou Virginide, chacun puisse dire que ce sont les-autres-en-face qui vieillissent plus vite.
Utilisation d'un diagramme
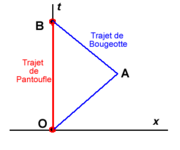
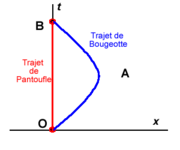
En relativité restreinte on a l'habitude d'utiliser des diagrammes sur lesquels on reporte des événements, par exemple ceux rattachés à la trajectoire d'une particule. Alors qu'en géométrie classique euclidienne on considérait deux axes (x, y) indiquant seulement la position géométrique de la particule, dans un diagramme relativiste il est nécessaire de conserver un axe pour le temps t. L'autre axe restera spatial et mesurera la distance x de l'objet à un point origine (le mouvement étant supposé se faire le long de l'axe considéré). La figure montre un tel diagramme pour analyser les lignes d'univers (c'est ainsi qu'on appelle la trajectoire d'un mobile dans un repère espace-temps) des deux jumeaux.
L'axe vertical représente le temps t et l'axe horizontal, spatial, représente la distance x parcourue par Bougeotte. On se place dans le repère terrestre de Pantoufle.
On voit sur le schéma qu'il y a deux trajets différents reliant l'événement de départ O (le départ de la fusée) et le retour sur Terre B du voyageur de Langevin. L'un est rectiligne sur le diagramme, celui de Pantoufle. L'autre est constitué de la ligne brisée OAB (ou plus généralement de toute ligne courbe reliant O à B). Ce que nous cherchons à comparer sur le diagramme, c'est la durée propre le long du trajet courbe de Bougeotte et celle le long du trajet direct de Pantoufle.
Attention ! On pourrait croire que la durée du trajet direct est plus courte que celle du trajet indirect mais il n'en est rien ! En géométrie euclidienne la distance la plus courte entre deux points est bien la distance directe mais en géométrie relativiste c'est le contraire qui est vrai, comme nous l'avons indiqué plus haut. En effet le long d'un trajet infinitésimal (Δx, δt), le carré du temps propre Δτ est donné par la relation
avec un signe « - » devant le carré de Δx. Ce signe « - » change tout car il entraîne que la durée propre est toujours plus petite que l'intervalle temporel Δt mesuré dans n'importe quel repère. Par conséquent, en relativité restreinte, sur un diagramme espace-temps la durée propre qui sépare les deux événements O et B est toujours plus petite le long d'un trajet courbe que le long du trajet direct OB (voir Géométrie dans l'espace de Minkowski).
Ici le temps τ écoulé le long du trajet indirect OAB suivi par Bougeotte est plus petit que le temps t mesuré par Pantoufle (représenté par le segment de droite OB). Le temps propre infinitésimal étant donné par la formule ci-dessus, le temps propre total mesuré par Bougeotte sera
où nous avons simplement remplacé Δx par vΔt.
Dans le cas général, avec une vitesse variable, il suffira de faire le calcul de l'intégrale le long du chemin spatio-temporel parcouru avec une vitesse v(t).
Dans le cas où le voyage en fusée se fait en deux segments de droite à vitesse v constante, on a immédiatement le résultat
Le temps dans la fusée est plus petit que le temps terrestre par le facteur
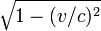 . Pour une vitesse v égale aux 3/5 de la vitesse de la lumière (soit v=0,6 c, ce qui est évidemment tout à fait impossible à réaliser) le facteur de réduction est de 4/5=0,8. En sens inverse le facteur de dilatation est de 5/4. Ainsi si Bougeotte voyageait 40 ans, il retrouverait son frère Pantoufle vieilli de 50 ans.
. Pour une vitesse v égale aux 3/5 de la vitesse de la lumière (soit v=0,6 c, ce qui est évidemment tout à fait impossible à réaliser) le facteur de réduction est de 4/5=0,8. En sens inverse le facteur de dilatation est de 5/4. Ainsi si Bougeotte voyageait 40 ans, il retrouverait son frère Pantoufle vieilli de 50 ans.L'analyse du paradoxe en termes d'effet Doppler transversal
Le paradoxe des jumeaux peut être analysé de façon élégante et instructive[7] en utilisant l'effet Doppler sous une forme différente de son aspect traditionnel, en faisant abstraction de la vitesse radiale et en ne conservant que l'effet de dilatation des durées.
L'effet Doppler relativiste est surtout connu pour son aspect longitudinal, correspondant au décalage vers le rouge ou vers le bleu selon que la source s'éloigne ou se rapproche de l'observateur. On trouve de nombreuses présentations[8] du paradoxe des jumeaux utilisant cette différence de fréquences entre les phases aller et retour. Plus rare est l'illustration par l'emploi de l'effet Doppler transversal. Rappelons que si l'effet Doppler longitudinal classique dépend de la composante radiale de la vitesse, l'effet transversal dépend de la vitesse totale et correspond toujours à une diminution de la longueur d'onde du signal reçu.
Comme précédemment Pantoufle reste sur Terre pendant que son frère jumeau Bougeotte fait un voyage vers une planète lointaine à une vitesse proche de celle de la lumière puis revient sur Terre dans les mêmes conditions. Dans notre expérience les jumeaux observent tous les deux un pulsar lointain dont l'éclat varie périodiquement. On suppose le pulsar très éloigné de la Terre et également de la fusée, à chaque instant de son parcours. Celle-ci se déplace selon une direction perpendiculaire à la direction Terre-pulsar, l'éloignement permettant d'affirmer que la lumière du pulsar atteint la fusée perpendiculairement à sa trajectoire (dans le repère de la Terre[9] ) et qu'un signal donné du pulsar atteint la Terre et la fusée au même moment (même : dans le référentiel terrestre).
L'intérêt de cette présentation réside en ce que le pulsar, supposé immobile dans le référentiel de la Terre, joue le rôle d'une horloge visible à la fois de la Terre et de la fusée, représentant une sorte de phare cosmique battant à un rythme imperturbable[10], de fréquence propre fem (en cycles par seconde). Autre intérêt : comme les jumeaux observent le même objet et reçoivent ses éclairs au même moment (dans le référentiel terrestre), l'expérience rétablit une certaine symétrie entre eux deux, à ceci près que l'un est au repos et l'autre en mouvement. Comment Pantoufle et Bougeotte vont-ils percevoir ce pulsar au cours du voyage ?
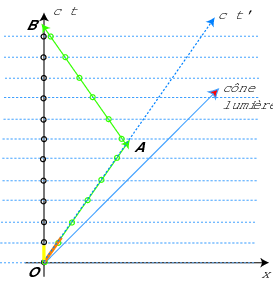 Diagramme d'espace-temps du voyage, marqué par les flashs du pulsar. Le pulsar, loin du plan (Ox,ct), marque tout le plan de ses flashs réguliers (lignes pointillées horizontales : éclairage simultané de l'axe Ox). Les unités de temps des repères Terre et fusée sont respectivement en jaune et marron. Les petits cercles sont les événements réception des flashs pour les deux observateurs.
Diagramme d'espace-temps du voyage, marqué par les flashs du pulsar. Le pulsar, loin du plan (Ox,ct), marque tout le plan de ses flashs réguliers (lignes pointillées horizontales : éclairage simultané de l'axe Ox). Les unités de temps des repères Terre et fusée sont respectivement en jaune et marron. Les petits cercles sont les événements réception des flashs pour les deux observateurs.
Compte-tenu de la géométrie décrite ci-dessus et de la formule de l'effet Doppler relativiste dans la direction θ’ mesurée dans le repère Terre-pulsar :
la fusée perçoit les flashs du pulsar avec une fréquence décalée par l'effet Doppler transversal :
La fréquence perçue est plus grande que la fréquence propre, autrement dit pour le passager de la fusée les éclairs du pulsar se succèdent plus rapidement (avec une période plus courte).
Le nœud de l'explication du paradoxe des jumeaux en termes d'effet Doppler transversal réside dans la remarque suivante : puisque les deux observateurs reçoivent les signaux du pulsar en même temps (dans le repère Terre-pulsar) et qu'ils se retrouvent au même point, ils auront vu les mêmes éclairs et en auront forcément comptabilisé le même nombre. Comment cela se peut-il ? La réponse est facile : Bougeotte aura comptabilisé avec un pulsar au rythme plus rapide pendant un laps de temps plus court le même nombre d'éclairs que Pantoufle observant pendant un temps plus long un pulsar plus lent.
Par conséquent le facteur γ-1 ≡ [1 - (v2/c2)]1/2 de réduction de la période dans le repère de la fusée est également le facteur de réduction de la durée du voyage. Nous retrouvons ainsi par cette méthode Doppler le résultat antérieur sur la différence dans la mesure de la durée du voyage déduit des formules de Lorentz.
Voici une application numérique (correspondant par ailleurs à une expérience imaginaire, impossible à réaliser « pour de vrai », reprenant les chiffres de la section précédente). Considérons une fusée se déplaçant à une vitesse égale à (3/5)c à laquelle correspond un facteur de contraction (1 - 9/25)1/2 = 4/5. Supposons que Pantoufle voie le pulsar émettre ses éclairs au rythme de 1 par seconde (et en perçoive donc 60 par minute). Alors Bougeotte dans sa fusée verra se succéder les éclairs au rythme de 1 toutes les 4/5=0,8 seconde sur son horloge (et en comptera donc 60 en 48 secondes, ou 75 en 60 secondes). Au retour sur Terre, disons après 50 ans pour Pantoufle et par conséquent 40 ans pour Bougeotte, le nombre d'éclairs compté par Pantoufle, proportionnel à (50/1) (an/seconde) est bien égal à celui compté par Bougeotte, proportionnel pour sa part à (40/0,8) (an/seconde) (on a bien 40/0,8=40×5/4=50).
Calcul du rajeunissement relativiste dans une fusée accélérée
Il est souvent dit que c'est l'accélération subie par Bougeotte qui cause la dissymétrie entre les deux jumeaux et que pour traiter ce problème il faudrait faire appel à la relativité générale, seule capable de gérer les accélérations. Or si l'accélération communiquée à la fusée est bien quelque part la cause de la dissymétrie, car pour faire demi-tour il faut allumer des moteurs, il faut toutefois se défaire de cette fausse idée selon laquelle la relativité restreinte ne pourrait pas prendre en compte les accélérations. Cette juste remise en question des idées reçues est présentée par Misner, Thorne et Wheeler[11], qui montrent qu’on peut analyser des mouvements accélérés en se servant uniquement de la relativité restreinte[12]. Nous allons montrer ici qu'on peut effectivement traiter le cas d'une fusée accélérée sans faire appel à la relativité générale.
Nous suivons ici la présentation de Taylor et Wheeler[13].
Tout d'abord comment la relativité restreinte traite-t-elle les repères accélérés ? Réponse : elle rapporte à chaque instant le mouvement du mobile considéré au repère inertiel qui à cet instant précis le côtoie à la même vitesse. Autrement dit la relativité restreinte utilise à chaque instant le repère inertiel avec lequel le mobile est en quelque sorte en coïncidence. De cette façon la théorie continue à se servir de repères galiléens et peut appliquer les formules de transformation correspondantes.
Considérons donc une fusée (imaginaire !) dont les passagers seraient soumis grâce à de puissants moteurs à une accélération constante g égale à celle de la gravité que nous subissons sur Terre. Numériquement g=10 (m/s)/s = 1000 (cm/s)/s. Nous voulons savoir en combien de temps cette fusée va parcourir telle distance, en sachant d'avance que le temps mesuré par les passagers de la fusée sera plus court que le temps mesuré par les terriens.
Remarquons que l'accélération de la fusée n'est pas égale à g dans le repère terrestre. L'accélération g est mesurée dans la fusée par exemple grâce à un pèse-personne embarqué. Comme nous l'avons dit plus haut, la relativité restreinte énonce que la fusée est accélérée par rapport au repère (le train de fusées) qui à l'instant considéré possède la même vitesse qu'elle. Ce repère joue le rôle d'un repère inertiel instantané. Dans ce repère la vitesse de la fusée passe de la valeur 0 à la valeur dv pendant le temps dτ. Et dire que l'accélération vaut g signifie que :
En relativité restreinte on sait que les vitesses ne sont pas additives. Si d'une fusée se déplaçant à la vitesse v par rapport à la Terre est tiré vers l'avant un boulet de canon à la vitesse w (par rapport à cette fusée), la vitesse du boulet par rapport à la Terre n'est pas v + w. On montre que la quantité pertinente est en réalité un angle θ, qu'on peut appeler le paramètre angulaire de vitesse, défini par la relation :
Autrement dit :
La propriété principale de ce paramètre angulaire de vitesse est qu'il est additif. Ainsi notre boulet tiré ci-dessus de la fusée a par rapport à la Terre un paramètre de vitesse θ égal à la somme des paramètres de vitesse de la fusée par rapport à la Terre, soit θfus, et du boulet par rapport à la fusée, soit θ' :
Revenons à l'accélération de la fusée. Dans le repère coïncidant la vitesse de la fusée passe de 0 à dv et à cette vitesse élémentaire dv correspond le paramètre de vitesse élémentaire dθ donné par la formule écrite ci-dessus :
On a donc la relation :
qui s'intègre immédiatement comme :
Cette formule donne le paramètre angulaire de vitesse θ de la fusée par rapport au repère terrestre en fonction du temps propre τ de l'astronaute dans sa fusée.
Quelle est maintenant la trajectoire de la fusée dans le repère terrestre ?
En tenant compte de la relation entre vitesse v et paramètre angulaire de vitesse θ et de la définition classique de la vitesse v=dx/dt où x est la distance parcourue par la fusée dans le repère terrestre et t le temps terrestre, on a :En tenant compte de la dilatation du temps (dt est toujours plus grand que dτ) :
on aboutit à la formule suivante donnant la distance dx mesurée dans le repère terrestre parcourue pendant le laps de temps dτ de l'astronaute :
Cette expression s'intègre facilement pour donner le résultat :
Cette formule résout le problème posé. Elle donne la distance x parcourue par la fusée dans le repère terrestre pendant la durée τ mesurée par les astronautes.
En ce qui concerne les durées, on a :
et par conséquent :
formule qui donne le rajeunissement relativiste en montrant bien que (gt/c) est plus grand que (gτ/c) et donc que la durée t est plus grande que la durée τ.
Application numérique
L'application numérique qui suit est une illustration seulement théorique car aucune technologie ne peut fournir le moyen de communiquer physiquement par accélération à un vaisseau spatial une vitesse proche de celle de la lumière, nécessaire pour rendre appréciable le ralentissement du temps.
Sachant qu'une année fait environ 3×107 secondes, que c égale 3×1010 centimètres par seconde et que g vaut 103 centimètres-par-seconde par seconde, exprimons les temps en années et les distances en années-lumière. On trouve alors que le temps (c/g) vaut une année, que la distance (c2/g) vaut une année-lumière et que la distance en années-lumière parcourue pendant le temps T mesuré par les astronautes (et compté en années) est donnée par la formule numérique :
- x (en années-lumière) = cosh(T ) - 1 .
La durée du trajet mesurée sur Terre est :
- t = sinh(T ) .
Les durées et distances parcourues théoriques sont données dans le tableau suivant :
Trajet d'une fusée subissant une accélération constante g dans son propre référentiel Durée T du trajet dans le repère de la fusée
(en années)Durée t pour les terriens
(en années)Distance x parcourue dans le repère terrestre
(en années-lumière)1 1,2 0,54 2 3,6 2,8 5 74 73 10 11 000 11 000 12,21 100 000 100 000 En théorie, le voyageur utilisant une hypothétique fusée accélérée pourrait donc traverser la Galaxie entière (qui fait quelque cent mille années-lumière de diamètre) en une douzaine d'années. Sa vitesse maximum serait pratiquement égale à celle de la lumière (à 10-11 près). L'impossibilité de communiquer une telle vitesse à un engin spatial ne doit pas cacher la réalité du phénomène de la dilatation des durées : comme il est calculé ailleurs, la bouffée de particules de très haute énergie, issue par exemple d'une explosion d'une supernova, met 100 000 ans pour l'observateur terrestre pour traverser la Galaxie entière à une vitesse quasiment égale à celle de la lumière, mais cette durée ne compte pour les particules que quelques dizaines de secondes de leur temps propre.
Confirmations expérimentales
Comme on vient de le dire, la preuve la plus évidente de la dilatation du temps est la différence des durées de vie des muons des rayons cosmiques et de ceux produits en laboratoire. Mais à partir de 1971, des vérifications directes du paradoxe furent possibles : des avions à réaction embarquèrent des horloges atomiques tandis que des horloges similaires synchronisées restaient au sol. Lorsque les avions suivaient le mouvement de la Terre, à leur retour, les horloges embarquées avaient retardé de quelques milliardièmes de seconde sur les horloges restées au sol, un écart en parfait accord avec la théorie de la relativité (des corrections plus fines liées à la relativité générale ont également été mesurées). Le décalage s'inverse si l'avion parcourt la Terre dans le sens opposé à sa rotation (pour bien comprendre ces expériences, il faut tenir compte de ce que le référentiel terrestre n'est lui-même pas galiléen). Toutes corrections faites, ces expériences n'ont fait que confirmer, avec une précision de plus en plus grande, les prédictions de la théorie[14].
Résumé et conclusion
On peut regretter que le paradoxe des jumeaux ait été exploité dans le sens de la mise en évidence d'une prétendue contradiction interne de la théorie de la relativité restreinte, une contradiction qui invaliderait la théorie d'Einstein. Nous avons vu ici que cet aspect négativiste est infondé. D'ailleurs d'autres prétendus paradoxes ont été inventés mais aucun ne résiste à une analyse juste des situations correspondantes[15].
Dans le paradoxe des jumeaux la contradiction supposée viendrait du fait que, tous les mouvements étant supposés relatifs, les deux jumeaux vivraient des histoires symétriques et par conséquent aucun ne pourrait se retrouver plus jeune que l'autre. Nous avons vu comment lever la situation paradoxale apparente du rajeunissement de Bougeotte par rapport à Pantoufle. En vérité les deux jumeaux ne jouent pas des rôles symétriques puisque Pantoufle sur Terre est le seul à être resté au repos par rapport à un seul référentiel galiléen tandis que Bougeotte a fait un demi-tour et s'est trouvé en coïncidence avec au moins deux repères galiléens différents. Les repères de Pantoufle et de Bougeotte ne sont pas interchangeables.
Autres paradoxes en physique
- Petites expériences de pensée d'Einstein,
- Le paradoxe du train,
- Le démon de Maxwell,
Notes et références
- ↑ Comme par exemple dans le chapitre 6 « Le paradoxe des jumeaux » de l'Introduction à la relativité par James H. Smith, 1965, réédité en 1997 chez Masson, ISBN 2-225-82985-3, traduit par Philippe Brenier, préfacé par Jean-Marc Lévy-Leblond.
- ↑ (en) Albert Einstein, 1911, cité par (en) Robert Resnick et David Halliday, Basic Concepts in Relativity, Macmillan, New York, 1992
- ↑ (fr)Paul Langevin, « L’évolution de l’espace et du temps », dans Scientia, no 10, 1911, p. 31-54 [texte intégral]
- ↑ (fr) Michel Paty, « Paul Langevin (1871-1946), la relativité et les quanta », dans Bulletin de la Société Française de Physique, no 119, mai 1999, p. 15-20 [texte intégral]
- ↑ a , b et c Un "top" horaire est émis en un point O à disons midi. Comme chaque observateur A connaît sa distance OA au point O il sait le temps OA/c que met le signal horaire pour venir de O et peut donc ajuster son heure à midi + (OA/c) à réception du top.
- ↑ Si on préfère cette image-ci du repère terrestre, on peut encore penser à un ensemble de « bouées de l'espace », stations réparties le long d'un axe à intervalle régulier (une bouée étant séparée de la suivante par une année de lumière par exemple), possédant une horloge marquant le temps terrestre et abritant une personne chargée de consigner tous les événements, notamment le passage de visiteurs, sur un carnet de bord.
- ↑ voir E.F. Taylor, J.A. Wheeler, A la découverte de l'espace-temps, Dunod, Paris, 1970, page 233 ou (en) E.F. Taylor, J.A. Wheeler, Spacetime Physics, Second edition, W.H. Freeman and Company, 1992, page 264
- ↑ voir par exemple le voyage dans le futur des autres.
- ↑ Il faut noter ici que le phénomène d'aberration implique que la fusée verra, elle, la lumière du pulsar lui arriver de l'avant dans la direction θ donnée par cosθ=v/c selon les formules complètes de l'effet Doppler relativiste.
- ↑ On ne prétend pas que le pulsar batte une cadence absolue puisqu'en l'occurrence il s'agit d'une pulsation de temps terrestre, mais on peut dire néanmoins que Bougeotte, s'il voit la fréquence varier, ne pourra pas soutenir que c'est le pulsar qui, intrinsèquement, aura changé sa fréquence de clignotement.
- ↑ (en) C. W. Misner, Kip Thorne & John Wheeler : Gravitation, Freeman & Co. (San Francisco-1973), page 163-167.
- ↑ Après tout, les équations de la relativité restreinte suffisent à décrire les particules tournoyant dans les accélérateurs.
- ↑ (en)E.F. Taylor, J.A. Wheeler, Spacetime Physics, W.H. Freeman and Company, 1966, page 97
- ↑ Article de Loïc Villain sur le site de Futura-Science [1]
- ↑ (en) voir les paradoxes analysés par E.F. Taylor et J.A. Wheeler dans leur livre Spacetime Physics, W.H. Freeman and Company, 1966
Liens internes
Voir aussi
- (en)Voir le chapitre 4 Trip to Canopus du livre de Taylor et Wheeler, Spacetime Physics, Introduction to special relativity, second edition, W.H. Freeman and Company, 1992, pp 121-136
- Théorie de la Relativité Restreinte, V. Ougarov, Deuxième Edition, Editions Mir, Moscou, Traduction française Editions Mir, 1979.
- The Twin Paradox par Michael Weiss
- Portail de la physique
Catégories : Albert Einstein | Expérience de pensée | Paradoxe physique | Relativité
Wikimedia Foundation. 2010.

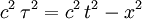
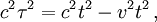
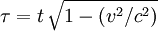
![t = \tau\, /\,\sqrt{1 - (v^2/c^2)}\equiv \gamma\tau \ \qquad \text{avec} \qquad\gamma = [1 - (v^2/c^2)]^{-1/2}\ .](/pictures/frwiki/51/313500ca60fbc89039dd707cf4e6efc1.png)
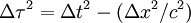
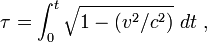
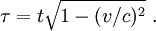
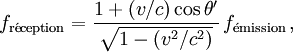
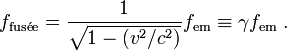
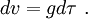
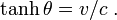
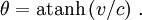
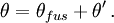
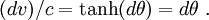
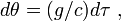
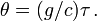
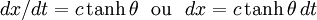
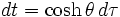
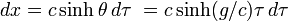
![x = (c^2/g)[\cosh(g\tau/c) - 1]\ .](/pictures/frwiki/56/8f14c3d935ef1e2d006e5b49b3a74dcb.png)