Produit fibré

Produit fibré
Diagramme commutatif traduisant la propriété universelle du produit fibré.

En mathématiques, le produit fibré est une opération entre deux ensembles munis tous deux d'une application vers un même troisième ensemble. Sa définition s'étend à certaines catégories en satisfaisant une propriété universelle de factorisation de diagrammes, en dualité avec la somme amalgamée.

Le produit fibré est utilisé notamment en géométrie algébrique pour définir le produit de deux schémas, ou en topologie algébrique pour construire, à partir d'un espace fibré (tel un revêtement), un autre espace de même fibre, le fibré induit (en), en remontant le long d'une application entre les deux bases, d'où l'appellation en anglais pullback (« tiré en arrière ») parfois utilisée en français.

Définition ensembliste

Étant données deux applications vers un même ensemble[1] :

A \stackrel{f}{\longrightarrow}\!\! \begin{array}[b]{c} E \\ \downarrow^p\!\!\! \\ B \end{array}

le produit fibré de A et E au-dessus de B est défini comme l'ensemble des couples (a;e) du produit cartésien A×E dont les composantes ont même image : f(a) = p(e). Il se note :

A \underset{B}{\times} E

Le produit fibré étant un sous-ensemble du produit cartésien, les projections sur chaque facteur permettent de compléter le carré commutatif :

\begin{array}{crc} A \underset{B}{\times} E & \stackrel{\pi_E}{\to} & E \\ \downarrow\!\! {\scriptstyle \pi_A}\!\!\!\!\!\! & & \downarrow \\ A & \!\!\!\! \longrightarrow & B\end{array}

Dans des catégories ensemblistes, telles celles des espaces topologiques ou des espaces vectoriels, le produit fibré constitue lui-même un objet de la catégorie.

Propriété universelle

Avec les notations de la partie précédente, si X est un ensemble muni d'applications vers A et E qui permettent de construire un carré commutatif :

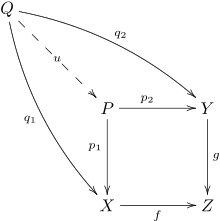
\begin{array}{crc} X & \stackrel{p_E}{\longrightarrow} & E \\ \downarrow\!\! ^{p_A}\!\!\!\!\!\! & & \downarrow \\ A & \longrightarrow & B\end{array}

alors il existe une unique application i de l'ensemble X vers le produit fibré qui factorise le diagramme :

p_A = \pi_A\circ i \qquad p_E = \pi_E\circ i

Autrement dit, le produit fibré est la limite (au sens des catégories) du diagramme formé à l'aide des deux applications initiales f et p. Il est aussi possible de le voir comme le produit (au sens des catégories) dans une catégorie des morphismes vers B.

Plus généralement, le produit fibré dans une catégorie quelconque est la limite d'un tel diagramme, lorsqu'elle existe, ce qui est le cas dans les catégories abéliennes.

Notes et références

  1. ↑ Les notations utilisées viennent du fait que si l'application p est la projection d'un espace fibré sur sa base, le produit fibré muni de sa projection sur A constitue un espace fibré de même fibre.

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Produit fibré de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Produit fibre — Produit fibré Notations Exemple de représentation d un produit fibré (Pour des détails sur les notions ci dessous, voir l article sur les catégories.) est la classe des flèches de la catégorie …   Wikipédia en Français

  • Produit (catégorie) — Dans une catégorie, le produit peut s exprimer par une propriété universelle ou de manière équivalente comme foncteur représentable. Définition produit Soit C une catégorie et une famille d objets de C. On cherche un objet X ainsi qu une famille… …   Wikipédia en Français

  • Produit tensoriel d'algèbres — En mathématique, le produit tensoriel de deux algèbres est une nouvelle algèbre. Définition Soit R un anneau commutatif. Soient A,B deux R algèbres (non nécessairement commutatives). On peut les considérer comme des R modules et construire le… …   Wikipédia en Français

  • Fibre vectoriel — Fibré vectoriel En topologie différentielle, un fibré vectoriel est une construction géométrique ayant une parenté avec le produit cartésien, mais apportant une structure globale plus riche. Elle fait intervenir un espace topologique appelé base… …   Wikipédia en Français

  • Fibré Vectoriel — En topologie différentielle, un fibré vectoriel est une construction géométrique ayant une parenté avec le produit cartésien, mais apportant une structure globale plus riche. Elle fait intervenir un espace topologique appelé base et un espace… …   Wikipédia en Français

  • Fibre De Verre — Ensemble de fibres de verre La fibre de verre est un filament de verre extrêmement fin. Par extension, les matériaux composites renforcés de cette fibre (généralement associés à polymères) sont aussi appelé fibre de verre. Sommaire …   Wikipédia en Français

  • Fibre principal — Fibré principal En topologie, de manière informelle, un fibré principal sur un espace topologique X est un espace ressemblant localement à un produit de X par un espace homogène, un espace topologique sur lequel agit librement un groupe… …   Wikipédia en Français

  • Fibré Principal — En topologie, de manière informelle, un fibré principal sur un espace topologique X est un espace ressemblant localement à un produit de X par un espace homogène, un espace topologique sur lequel agit librement un groupe topologique. En… …   Wikipédia en Français

  • Fibre de coco — La fibre de coco ou coir (de kayaru, corde en malayâlam) est une fibre végétale, naturelle qui entoure et protège la noix de coco, fruit du cocotier. A l extérieur de la noix, sous une enveloppe lisse, de couleur vert clair ou orange lorsque le… …   Wikipédia en Français

  • Fibre Optique Noire — La fibre optique noire désigne une fibre optique brute installée mais qui n est pas encore activée, ni à plus forte raison, utilisée. Elle est appelée ainsi car elle n est pas encore alimentée par une source lumineuse. On retrouve beaucoup de… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”