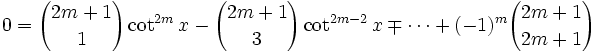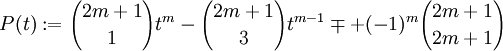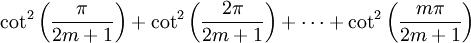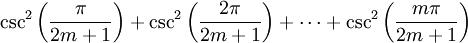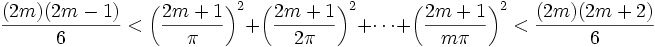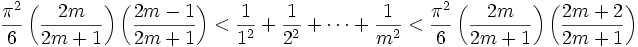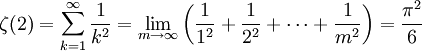- Problème de Mengoli
-
Problème de Bâle
En mathématiques, le problème de Bâle (connu parfois aussi sous le nom de problème de Mengoli) est un problème célèbre dans la théorie des nombres, posé en premier par Pietro Mengoli en 1644, et résolu par le mathématicien suisse Leonhard Euler en 1735, dont Bâle était la ville natale. Le problème résistait aux attaques des mathématiciens éminents de l'époque, ainsi, la solution d'Euler lui apporta une notorité immédiate à l'âge de 28 ans. Il a considérablement généralisé le problème et ses idées furent reprises par le mathématicien allemand Bernhard Riemann dans son article de 1859, dans lequel il a défini sa fonction ζ et a démontré ses propriétés de base.
Le problème demande la valeur exacte de la somme de la série :
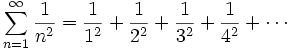
Celle-ci est approximativement égale à 1,64493406684822643. Vue la lente convergence de la série, une telle valeur approchée n'a pu être trouvée qu'en mettant en oeuvre des méthodes d'accélération de convergence, ce qui est fait notamment par Stirling[1] en 1730 et Euler[2] en 1731. Euler[3],[4] trouva finalement la somme exacte
Il annonça cette découverte en 1735. Ses arguments étaient basés sur des manipulations qui ne furent pas justifiées, et ce n'est que dix ans plus tard qu'il fut capable de produire une démonstration rigoureuse.
Euler attaque le problème
La déduction originale d'Euler de la valeur π2 / 6 est intelligente et originale. Il développa essentiellement des observations sur les polynômes finis et assura que ces mêmes propriétés sont toujours vraies pour les séries infinies. Bien sûr, le raisonnement original d'Euler requiert une justification, mais même sans justification, en obtenant simplement la valeur correcte, il fut capable de la vérifier numériquement par rapport aux sommes partielles de la série. La concordance qu'il observa lui inspira suffisamment confiance pour annoncer son résultat à la communauté mathématique.
Pour suivre l'argument d'Euler, rappelons le développement en série de Taylor de la fonction sinus
En divisant par
 , nous avons
, nous avonsMaintenant, les racines de sin(x) / x apparaissent précisément pour
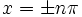 , où
, où 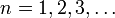 . Supposons audacieusement que nous puissions exprimer cette série infinie comme un produit de facteurs linéaires donnés par ses racines, comme nous le faisons pour les polynômes finis :
. Supposons audacieusement que nous puissions exprimer cette série infinie comme un produit de facteurs linéaires donnés par ses racines, comme nous le faisons pour les polynômes finis :Si nous multiplions formellement ce produit et factorisons tous les termes
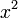 , nous voyons que le coefficient de x2 de sin(x) / x est
, nous voyons que le coefficient de x2 de sin(x) / x estMais, à partir du développement de la série infinie originale de sin(x) / x, le coefficient de x2 est
Ces deux coefficients doivent être égaux ; ainsi,
En multipliant les deux cotés de cette équation par − π2, nous obtenons la somme des inverses des carrés d'entiers positifs.
La fonction Zeta de Riemann
La fonction zeta de Riemann
 est une des plus importante fonctions des mathématiques, à cause de sa relation avec la distribution des nombres premiers. La fonction est définie pour tout nombre complexe s avec une partie réelle > 1 par la formule suivante :
est une des plus importante fonctions des mathématiques, à cause de sa relation avec la distribution des nombres premiers. La fonction est définie pour tout nombre complexe s avec une partie réelle > 1 par la formule suivante :En prenant s = 2, nous voyons que
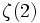 est égale à la somme des inverses des carrés d'entiers positifs :
est égale à la somme des inverses des carrés d'entiers positifs :Comment savons-nous qu'elle converge? Nous pouvons démontrer ceci avec l'inégalité suivante :
Or la série est une série à coefficients tous positifs. La série est donc croissante et bornée, donc convergente.
Ceci nous donne la limite supérieure
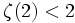 , mais la valeur exacte ζ(2) = π2 / 6 était inconnue pour un certain temps, jusqu'à ce que Leonhard Euler la calcule en 1735. Il peut être montré que
, mais la valeur exacte ζ(2) = π2 / 6 était inconnue pour un certain temps, jusqu'à ce que Leonhard Euler la calcule en 1735. Il peut être montré que  a une belle expression en nombres de Bernoulli quand s est un entier positif pair.
a une belle expression en nombres de Bernoulli quand s est un entier positif pair.Une démonstration rigoureuse
L'argument suivant prouve l'identité ζ(2) = π2 / 6, où ζ(s) est la fonction Zeta de Riemann. C'est de loin, la démonstration la plus simple disponible ; car la plupart des démonstrations utilisent des résultats de mathématiques avancées, telle que les séries de Fourier, l'analyse complexe, et le calcul à plusieurs variables ; celle qui suit ne requiert même pas le calcul à une variable (bien qu'une limite soit prise à la fin).
Historique de la démonstration
L'origine de cette démonstration n'est pas claire. Elle apparaît dans le journal Eureka en 1982, attribuée à John Scholes, mais Scholes déclara qu'il avait appris la démonstration de Peter Swinnerton-Dyer, et dans tous les cas il maintient que la démonstration était un « savoir commun de Cambridge à la fin des années 1960 ».
Ce que vous avez besoin de connaître
Pour comprendre la démonstration, vous aurez besoin de comprendre les énoncés suivants :
La formule de De Moivre
Elle énonce que pour tout nombre réel x et tout entier n on a
- (cosx + isinx)n = cos(nx) + isin(nx)
Voir l'article formule d'Euler pour une démonstration.
La formule du binôme de Newton
Elle énonce que pour tout nombre réel x et y et tout entier positif n,
où nous avons les coefficients binomiaux
Article détaillé : factorielle.Elle se démontre par récurrence, voir l'article sur la formule du binôme.
Injectivité de la fonction cotangente carrée
La fonction réelle
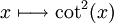 (où cot désigne la fonction cotangente) est injective dans l'intervalle [0,π / 2].
(où cot désigne la fonction cotangente) est injective dans l'intervalle [0,π / 2].Démonstration : Supposons cot2(x) = cot2(y) pour des certains x et y dans l'intervalle [0,π / 2]. En utilisant la définition de la cotangente pour
![x \in [0,\pi/2]](/pictures/frwiki/52/421d5aef0497e21c1d81312c40a84c12.png) on a
on apuis l'identité trigonométrique cos2(x) = 1 − sin2(x), nous voyons que sin2(x)(1 − sin2(y)) = sin2(y)(1 − sin2(x)). En soustrayant sin2(x)sin2(y) de chaque coté, nous avons sin2(x) = sin2(y). Comme la fonction sinus est toujours positive sur l'intervalle [0,π / 2], ceci veut dire que sin(x) = sin(y), mais cela est géométriquement évident (en regardant le cercle unité) que la fonction sinus est injective sur l'intervalle [0,π / 2]et donc que x = y.
Nombre de racines d'un polynôme
Si P est un polynôme de degré m, alors P n'a pas plus que m racines distinctes.
Démonstration : ceci est une conséquence de ce que, si r est racine de P, on peut écrire P sous la forme P(X) = (X − r)Q(X) avec Q un polynôme de degré m − 1.
Somme des racines d'un polynôme
Si
 , alors la somme des racines de P (comptées avec leurs multiplicités) est − am − 1 / am.
, alors la somme des racines de P (comptées avec leurs multiplicités) est − am − 1 / am.Démonstration : si am = 1, alors P(X) est égal au produit de tous les X − s, où s l'ensemble des racines de P. En développant ce produit, nous voyons que le coefficient de Xm + 1 est l'opposé de la somme de toutes les racines. Si
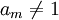 , alors nous pouvons diviser chaque terme par lui (comme P est de degré m, on a bien
, alors nous pouvons diviser chaque terme par lui (comme P est de degré m, on a bien 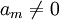 ), et l'on obtient un nouveau polynôme avec les mêmes racines, dont le premier coefficient est maintenant égal à 1; en appliquant l'argument précédent, on montre que la somme des racines de P est égale à la somme des racines de ce nouveau polynôme, c'est-à-dire − am − 1 / am
), et l'on obtient un nouveau polynôme avec les mêmes racines, dont le premier coefficient est maintenant égal à 1; en appliquant l'argument précédent, on montre que la somme des racines de P est égale à la somme des racines de ce nouveau polynôme, c'est-à-dire − am − 1 / amUne identité trigonométrique
L'identité trigonométrique cosec2(x) = 1 + cot2(x)
Démonstration : Ceci découle de l'identité fondamentale cos2(x) + sin2(x) = 1 après avoir été divisé par sin2(x).
Des inégalités
Pour tout nombre réel
![x \in ]0,\pi/2[](/pictures/frwiki/57/9d95f93176afeddbe3293bb17eaef5e9.png) , nous avons les inégalités cot2(x) < 1 / x2 < cosec2(x).
, nous avons les inégalités cot2(x) < 1 / x2 < cosec2(x).Démonstration : Premièrement, nous avons 0 < sin(x) < x < tan(x). Ceci peut être vu en examinant la figure suivante :
Maintenant, inversons tout cela et élevons au carré. Souvenons-nous que l'inégalité change de sens.
Une limite
Soit a, b, et c des nombres réels, avec a et c tous deux différents de zéro; alors la limite de la fonction (am + b) / (am + c) quand m tend vers l'infini est 1.
Démonstration : Divisons chaque terme par m, nous obtenons
Si nous divisons un nombre fixé par un grand nombre, le quotient tend vers zéro ; ainsi, le numérateur et le dénominateur du dessous tend vers a, et ainsi leur quotient tend vers 1.
Le théorème des gendarmes ou propriété de l'étau
Il énonce que si une fonction est « encadrée » entre deux autres fonctions, et que chacune de ces deux fonctions tendent vers une limite commune, alors la fonction « encadrée » tend aussi vers la même limite.
Pour une démonstration, voir l'article.
La démonstration
L'idée principale derrière la démonstration est de borner les sommes partielles
entre deux expressions, chacune tendra vers π2 / 6 quand m tend vers l'infini. Les deux expressions sont issues des identités impliquant la fonction cotangente et la fonction cosécante. Ces identités découlent à leur tour de la formule de De Moivre, et nous servent à établir ces identités.
Soit
![x\in ]0,\pi/2[](/pictures/frwiki/57/9d95f93176afeddbe3293bb17eaef5e9.png) , et soit n un entier positif. Alors, à partir de la formule de De Moivre et de la définition de la fonction cotangente, nous avons
, et soit n un entier positif. Alors, à partir de la formule de De Moivre et de la définition de la fonction cotangente, nous avonsA partir du théorème du binôme, nous avons
En combinant les deux équations et en égalisant les parties imaginaires, nous avons l'identité
Nous prenons cette identité et nous fixons n = 2m + 1, où m est un entier positif, et x = rπ / (2m + 1), où
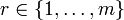 . Alors nx = rπ, donc sin(nx) = 0 , ainsi
. Alors nx = rπ, donc sin(nx) = 0 , ainsiCette équation est valable pour chacune des valeurs x = rπ / (2m + 1), où
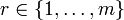 . Ces valeurs de x sont des nombres distincts strictement compris entre 0 et π / 2. Puisque la fonction cot2 est injective sur l'intervalle [0,π / 2], les nombres cot2(x) = cot2(rπ / (2m + 1)) sont par conséquent distincts pour
. Ces valeurs de x sont des nombres distincts strictement compris entre 0 et π / 2. Puisque la fonction cot2 est injective sur l'intervalle [0,π / 2], les nombres cot2(x) = cot2(rπ / (2m + 1)) sont par conséquent distincts pour 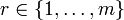 . Mais par l'équation précédente, chacun de ces nombres m distincts est une racine du polynôme de degré m suivant
. Mais par l'équation précédente, chacun de ces nombres m distincts est une racine du polynôme de degré m suivantCe qui veut dire que les nombres cot2(rπ / (2m + 1)), pour
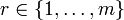 sont précisément les racines du polynôme P. Mais nous pouvons calculer la somme de ces racines directement en examinant les coefficients, et la comparaison montre que
sont précisément les racines du polynôme P. Mais nous pouvons calculer la somme de ces racines directement en examinant les coefficients, et la comparaison montre queEn substituant l'identité cosec2(x) = cot2(x) + 1, nous avons
Maintenant, considérons l'inégalité cot2(x) < 1 / x2 < cosec2(x). Si nous additionnons toutes ces inégalités pour chaque nombre x = rπ / (2m + 1), et si nous utilisons les deux identités ci-dessus, nous obtenons
En les multipliant par [π / (2m + 1)]2, cela devient
Lorsque m tend vers l'infini, la partie gauche et droite tendent chacune vers π2 / 6, donc, par le théorème des gendarmes,
Notes et références
- ↑ Jacobo Stirling, Methodus Differentialis sive Tractatus de Sommatione et Interpolatione Serierum Infinitarum, (1730), Prop.XI, exemple 1, p.55
- ↑ Euler, Opera Omnia, Series 1, Volume 14, pp.39-41, (E20 : De summatione innumerabilium progressionum)
- ↑ Euler, Opera Omnia, Series 1, Volume 14, pp.73-86, (E41 : De summis serierum reciprocarum)
- ↑ Euler, Opera Omnia Series 1, Volume 14, pp.177-186, (E63)
Voir aussi
Liens externes
- Une page dédiée à ζ(2) (en anglais)
- Une solution d'Euler sur le problème de Mengoli (en anglais) -- l'histoire plus longue (PDF)
- Comment Euler le fit (en anglais) (PDF)
- The infinite series of Euler and the Bernoulli's spice up a calculus class (PDF)
- Quatorze démonstrations de l'évaluation de ζ(2), (en anglais) compilées par Robin Chapman
- Portail des mathématiques
Catégorie : Analyse -
Wikimedia Foundation. 2010.

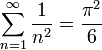
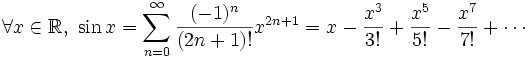
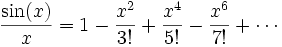
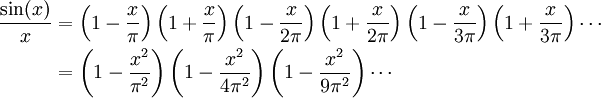
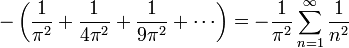

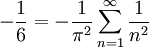
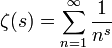

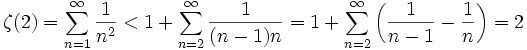
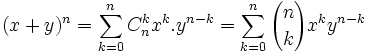
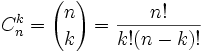
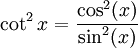

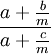

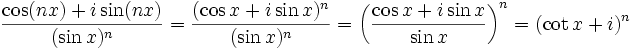
![\begin{align}(\cot x + i)^n &= {n \choose 0} \cot^n x + {n \choose 1} (\cot^{n-1} x)i + \cdots + {n \choose {n-1}} (\cot x)i^{n-1} + {n \choose n} i^n\\&= \left[ {n \choose 0} \cot^n x - {n \choose 2} \cot^{n-2} x \pm \cdots \right] \; + \; i\left[ {n \choose 1} \cot^{n-1} x - {n \choose 3} \cot^{n-3} x \mp \cdots \right]\end{align}](/pictures/frwiki/102/f86dd41a79555544a2dbe796e3fbd95c.png)
![\frac{\sin (nx)}{(\sin x)^n} = \left[ {n \choose 1} \cot^{n-1} x - {n \choose 3} \cot^{n-3} x \mp \cdots \right]](/pictures/frwiki/100/db786173c76be69fbf0946a3967e315e.png)