- À propos du nombre de nombres premiers inférieurs à une taille donnée
-
Sur le nombre de nombres premiers inférieurs à une taille donnée
Sur le nombre de nombres premiers inférieurs à une taille donnée (ou Über die Anzahl der Primzahlen unter einer gegebenen Grösse) est un article de 8 pages écrit par Bernhard Riemann et publié dans l'édition de novembre 1859 des Rapports mensuels de l'Académie de Berlin. Bien que ce soit le seul article qu'il ait publié sur la théorie des nombres, il contient des idées qui ont influencé des milliers de chercheurs depuis la fin du XIXe siècle jusqu'à nos jours.
Sommaire
Description
L'article contient d'abord des définitions, des arguments heuristiques, des esquisses de preuves et l'application de méthodes analytiques puissantes ; toutes celles-ci sont devenues des concepts essentiels et des outils de la théorie analytique des nombres moderne.
Parmi les nouvelles définitions introduites :
- le prolongement analytique de la fonction zêta de Riemann
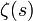 à tous les nombres complexes s différents de 1 ;
à tous les nombres complexes s différents de 1 ; - la fonction entière ξ(s) ;
- la fonction discrète J(x) définie pour
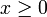 , qui est définie par J(0) = 0 et J(x), saute par bonds de
, qui est définie par J(0) = 0 et J(x), saute par bonds de 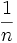 à chaque puissance de nombre premier
à chaque puissance de nombre premier 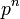 .
.
Parmi les preuves et les esquisses de preuves :
- deux preuves de l'équation fonctionnelle de ζ(s) ;
- la preuve de la représentation par produit de ξ(s) ;
- la preuve de l'approximation du nombre de racines de
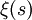 dont les parties imaginaires sont situées entre 0 et T.
dont les parties imaginaires sont situées entre 0 et T.
Parmi les conjectures produites :
- l'hypothèse de Riemann, tous les zéros (non triviaux) de
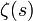 ont une partie réelle égale à
ont une partie réelle égale à  .
.
De nouvelles méthodes et techniques utilisées en théorie des nombres :
- prolongement analytique (différent du sens de Weierstrass) ;
- intégrale curviligne ;
- inversion de Fourier.
Riemann discuta aussi des relations entre
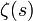 et la distribution des nombres premiers, utilisant la fonction J(x) essentiellement comme une mesure pour l'intégration de Stieltjes. Il obtint alors le résultat principal de l'article, une formule pour J(x), par comparaison avec
et la distribution des nombres premiers, utilisant la fonction J(x) essentiellement comme une mesure pour l'intégration de Stieltjes. Il obtint alors le résultat principal de l'article, une formule pour J(x), par comparaison avec 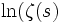 ). Riemann essaya alors d'élaborer une formule approximative pour la fonction de compte des nombres premiers
). Riemann essaya alors d'élaborer une formule approximative pour la fonction de compte des nombres premiers 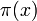 , bien qu'il admit lui-même être conscient du défaut de ses arguments.
, bien qu'il admit lui-même être conscient du défaut de ses arguments.Anecdote
L'article a eu une telle influence que la notation
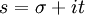 est utilisée pour noter un nombre complexe lors de l'étude de la fonction zeta à la place de la notation habituelle
est utilisée pour noter un nombre complexe lors de l'étude de la fonction zeta à la place de la notation habituelle 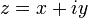 .
.Voir aussi
Articles connexes
Liens externes
Références
- H. M. Edwards, Riemann's Zeta Function, Dover, 1974, ISBN 0486417409
- Portail des mathématiques
Catégorie : Théorie analytique des nombres - le prolongement analytique de la fonction zêta de Riemann
Wikimedia Foundation. 2010.
