Principe Franck-Condon

Principe Franck-Condon
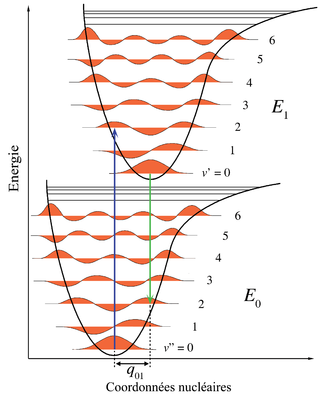Figure 1. Diagramme énergétique illustrant le principe Franck-Condon. Les transitions électroniques étant très rapides comparées aux mouvements nucléaires, les niveaux vibrationnels sont favorisés lorsqu'ils correspondent à une modification minime des coordonnées nucléaires. Les puits de potentiel indiqués sont ceux favorisant les transitions entre v = 0 et v = 2.

Le principe Franck-Condon est une loi de spectroscopie et chimie quantique qui explique l'intensité des transitions vibroniques. Les transitions vibroniques sont les modifications simultanées des niveaux d'énergie électroniques et de vibration d'un objet chimique dues à l'absorption ou à l'émission d'un photon d'énergie appropriée. Les états principaux qui lors d'une transition électronique ou d'une modification d'un niveau d'énergie vibrationnel à un autre seront plus susceptibles de se produire si les deux fonctions d'ondes vibrationnelles se superposent de manière significative.

Sommaire

Présentation générale

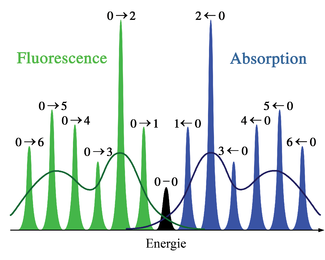Figure 2. Représentation schématique des spectres d'absorption et de fluorescence correspondant au diagramme d'énergie de la figure 1. La symétrie est due aux formes identiques des puits de potentiel des états fondamental et excité. Les lignes étroites ne peuvent être observées habituellement que dans les spectres de gaz dilués. Les courbes sombres représentent la dispersion inhomogène des mêmes transitions dans les liquides et solides. Les transitions électroniques entre les niveaux vibrationnels les plus bas des états électroniques (transition 0-0) ont la même énergie en absorption et en fluorescence.
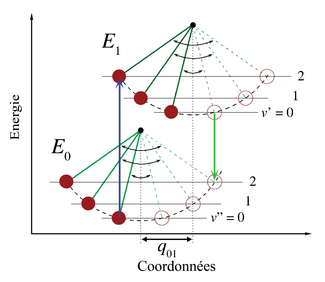Figure 3. Analogie au pendule semi-classique du principe Franck-Condon. Les transitions vibroniques sont permises aux points d'inversions classiques car la quantité de mouvement et les coordonnées nucléaires correspondent aux deux niveaux d'énergie représentés. Dans cette illustration, les transitions vibrationnelles 0-2 sont favorisées.

Le principe Franck-Condon possède une interprétation semi-classique bien connue basée sur les apports originaux de James Franck datant de 1927. Les transitions électroniques sont considérées comme instantanées dans l'échelle de temps des mouvements nucléaires ce qui fait que si la molécule considérée évolue vers un nouveau niveau vibrationnel durant une transition électronique, ce nouvel état doit être instantanément compatible avec les positions nucléaires et les quantités de mouvement du niveau vibrationnel de la molécule dans l'état électronique se créant. Dans la description semi-classique des vibrations (oscillations) d'un oscillateur harmonique simple, les conditions nécessaires peuvent s'obtenir aux points d'inversion, où la quantité de mouvement est nulle.

Selon l'IUPAC :
Classically, the Franck–Condon principle is the approximation that an electronic transition is most likely to occur without changes in the positions of the nuclei in the molecular entity and its environment. The resulting state is called a Franck–Condon state, and the transition involved, a vertical transition. The quantum mechanical formulation of this principle is that the intensity of a vibronic transition is proportional to the square of the overlap integral between the vibrational wavefunctions of the two states that are involved in the transition.

De manière classique, le principe Franck-Condon est l'approximation stipulant qu'une transition électronique est plus susceptible de se produire sans modifications des positions des noyaux dans l'entité moléculaire et son environnement. L'état résultant est appelé état Franck Condon, et la transition prise en compte, une transition verticale. La formulation quantique de ce principe est que l'intensité de la transition vibronique est proportionnelle au carré de l'intégrale de recouvrement entre les fonctions d'ondes vibrationnelles des deux états impliqués dans la transition.

IUPAC Compendium of Chemical Terminology, 2nd Edition (1997)


Dans la description quantique, les niveaux et fonctions d'ondes vibrationnels sont ceux des oscillateurs harmoniques quantiques, ou d'approximations plus complexes de l'énergie potentielle des molécules, comme le potentiel de Morse. La figure 1 illustre le principe Franck-Condon pour les transitions vibroniques dans une molécule avec des fonctions d'énergie potentielle de type Morse dans un état électronique fondamental et un excité. Dans l'approximation des températures basses, la molécule commence au niveau vibrationnel v = 0 de l'état électronique fondamental et par absorption d'un photon d'énergie adéquate, transite vers un état électronique excité. La configuration électronique du nouvel état peut provoquer un décalage de la position d'équilibre des noyaux constituant une molécule. Dans la figure, ce décalage dans les coordonnées atomiques entre l'état fondamental et le premier état excité est nommé q 01. Dans le cas le plus simple de la molécule diatomique, l'axe des coordonnées nucléaires réfère à la séparation internucléaire. La transition vibronique est indiquée par une flèche verticale en raison du postulat de la constance des coordonnées nucléaires durant la transition. La probabilité que la molécule puisse se trouver finalement dans un niveau vibrationnel particulier est proportionnelle au carré du recouvrement (vertical) des fonctions d'ondes vibrationnelles des états original et final (voir la formulation quantique dans la partie dédiée ci-dessous). Dans l'état électronique excité, les molécules se relaxent rapidement dans le niveau vibrationnel le plus bas (loi de Kasha), et à partir de là rejoignent l'état électronique de plus basse énergie par émission photonique. Le principe Franck-Condon s'applique de manière égale à l'absorption et à la fluorescence.

L'applicabilité du principe Franck-Condon à la fois dans l'absorption et la fluorescence, avec la loi de Kasha, conduit à une symétrie approchée par réflexion (figure 2). La structure vibrationnelle des molécules dans un gaz froid et peu dense est bien plus marquée en raison de l'absence d'élargissement inhomogène des transitions individuelles. Les transitions vibroniques sont représentées dans la figure 2 comme étroites, avec des profils lorentziens espacés régulièrement. Les espacements égaux entre niveaux vibrationnels n'existent que dans le cas d'un potentiel parabolique d'oscillateurs harmoniques simples. Dans le cas de potentiels plus réalistes, tels que ceux montrés figure 1, les écarts énergétiqes diminuent avec l'augmentation d'énergie vibrationnelle. Les transitions électroniques depuis et vers les états vibrationnels les plus bas sont parfois désignés comme des transitions 0-0 (zéro-zéro) et ont la même énergie en absorption et fluorescence.

Développement du principe

Dans un document publié en 1926 par les Transactions of the Faraday Society, James Franck discutait des mécanismes des réactions chimiques photo-induites. Le mécanisme présumé était l'excitation d'une molécule par un photon suivie par une collision avec une autre molécule durant la courte période d'excitation. La question qui se posait alors était de savoir si une molécule pouvait se décomposer en photoproduits en une seule étape, l'absorption du photon, et sans collision. Afin qu'une molécule se décompose en plusieurs produits, elle doit acquérir une énergie vibrationnelle photonique excédant l'énergie de dissociation qui est l'énergie pour rompre une liaison chimique. Cependant, comme on le savait à l'époque, les molécules absorbent seulement une énergie correspondant aux transitions quantiques permises et il n'existe pas de niveaux vibrationnels au-dessus du niveau d'énergie de dissociation du puits de potentiel. L'absorption d'un photon à haute énergie conduit à une transition dans un état d'énergie plus élevé au lieu de produire une dissociation. En étudiant la quantité d'énergie vibrationnelle qu'une molécule peut absorber lorsqu'elle est excitée dans un niveau d'énergie plus élevé, et si cette énergie vibrationnelle peut être suffisante pour dissocier la molécule, il dessina trois diagrammes représentant les modifications possibles dans les énergies de liaisons entre les états électroniques les plus bas et les plus hauts.

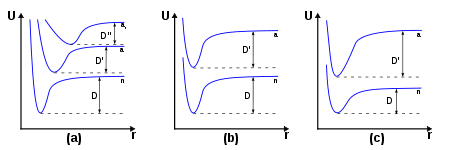Figure 4. Diagrammes inspirés de ceux produits par James Franck dans son article de 1926 pour illustrer sa réflexion sur le principe. Sont représentées les variations de potentiel U en fonction de r (rayon/coordonnée réactionnelle) dans trois cas distincts (a, b et c) pour différentes excitations traduites par les valeurs D. On pourra se reporter à la légende du dessin original indiquée dans le texte de l'article.

Dans son article, James Franck écrivait à propos de son schéma original (son explication s'applique à la figure 4) :
Diagram I. shows a great weakening of the binding on a transition from the normal state n to the excited states a and a' . Here we have D > D' and D' > D". At the same time the equilibrium position of the nuclei moves with the excitation to greater values of r. If we go from the equilibrium position (the minimum of potential energy) of the n curve vertically upwards to the a curves in Diagram I. the particles will have a potential energy greater than D' and will fly apart. In this case we have a very great change in the oscillation energy on excitation by light...

Le diagramme I montre un affaiblissement important de la liaison lors d'une transition depuis un état normal n vers les états excités a et a' . Nous avons ici D > D' et D' > D". Dans le même temps, la position d'équilibre des noyaux se déplace avec l'excitation vers des valeurs plus importants de r. Si nous allons de la position d'équilibre (le minimum d'énergie potentielle) de la courbe n verticalement vers les courbes a, les particules auront une énergie potentielle plus importante que D' et se détacheront. Dans ce cas, nous aurons une modification importante dans l'énergie d'oscillation causée par l'excitation lumineuse ...

James Franck 1926

James Franck réalisa que les modifications dans les niveaux vibrationnels pourraient être une conséquence de la nature instantanée de l'excitation vers les hauts niveaux d'énergie électronique et une nouvelle position d'équilibre pour le potentiel d'interaction nucléaire. Edward Condon étendit cette perception au-delà des photoréactions dans un article dans Physical Review en 1926 intitulé « A Theory of Intensity Distribution in Band Systems » (Une théorie de la distribution d'intensité dans les systèmes de bandes). Il y énonça la formulation semi-classique de manière tout à fait similaire à sa forme moderne. La première référence conjointe à James Franck et Edward Condon pour ce nouveau principe apparut dans la même série de 1926 de Physical Review dans un article sur la structure de bande du monoxyde de carbone de Raymond Birge.

Formulation quantique

Considérons une transition dipolaire électrique depuis un état vibrationnel initial (ʋ) de l'état électronique fondamental (ε),|\epsilon v\rangle, vers un état vibrationnel (ʋ' ) d'un état électronique excité (ε'), |\epsilon' v'\rangle (voir notation bra-ket). L'opérateur de dipôle moléculaire μ est déterminé par la charge (-e) et la localisation (ri) des électrons ainsi que par les charges (+eZj) et localisations (Rj) des noyaux :

\boldsymbol{\mu} = \boldsymbol{\mu} _e + \boldsymbol{\mu} _N = - e\sum\limits_i {\boldsymbol{r}_i } + e\sum\limits_j {Z_j \boldsymbol{R}_j }

L'amplitude de probabilité P pour la transition entre ces deux états est donnée par :

P = \left\langle \psi'\right|\boldsymbol{\mu} \left| \psi \right\rangle =\int {\psi'^ *} \boldsymbol{\mu} \psi d\tau

où \psi\ et \psi'\ sont, respectivement, les fonctions d'ondes globales des états initial et final. Ces fonctions d'ondes sont le produit des fonctions d'ondes vibrationnelle individuelle (dépendant des coordonnées spatiales du noyau), spatiale électronique et de spin :

\psi\ = \psi _e \psi _v \psi _s

Cette séparation des fonctions d'ondes électroniques et vibrationnelles est une conséquence de l'approximation Born-Oppenheimer et est le postulat fondamental du principe Franck-Condon. En combinant ces équations, on obtient une expression de l'amplitude de probabilité en termes de contributions vibrationnelle, spatiale électronique et de spin :

P=\left\langle \psi _e' \psi _v' \psi _s' \right|\boldsymbol{\mu} \left| \psi _e \psi _v \psi _s \right\rangle =\int {\psi _e'^ * \psi _v'^ * \psi _s'^ *} (\boldsymbol{\mu} _e + \boldsymbol{\mu} _N) \psi _e \psi _v \psi _s \, d\tau
{\color{White}P}=\int {\psi _e'^ * \psi _v'^ * \psi _s'^ *} \boldsymbol{\mu} _e \psi _e \psi _v \psi _s d\tau +\int {\psi _e'^ * \psi _v'^ * \psi _s'^ *} \boldsymbol{\mu} _N \psi _e \psi _v \psi _s d\tau
{\color{White}P}=\int { \psi _v'^ * } \psi _v d\tau_n \int { \psi _e'^ * } \boldsymbol{\mu} _e \psi _e d\tau_e \int { \psi _s'^ * } \psi _s d\tau_s \ \ + \int { \psi _e'^ * } \psi _e d\tau_e \int { \psi _v'^ * } \boldsymbol{\mu} _n \psi _v d\tau_v \int { \psi _s'^ * } \psi _s d\tau_s
{\color{White}P=} \begin{matrix} \underbrace{ {\color{White}.................} } \\ {}_{Facteur} \\ {}_{Franck-Condon} \end{matrix} \begin{matrix} \underbrace{ {\color{White}....................} } \\ {}_{Lois\ de\ selection} \\ {}_{orbitales} \end{matrix} \ \ \begin{matrix} \underbrace{ {\color{White}.................} } \\ {}_{Lois\ de\ selection} \\ {}_{de\ spin} \end{matrix} \ \ \ \ \begin{matrix} \underbrace{ {\color{White}................} } \\ {}_{||} \\ 0 \end{matrix}


La partie indépendante du spin de l'intégrale de départ est ici considérée comme un produit de deux intégrales :

\int\int { \psi _v'^ * } { \psi _e'^ * } \boldsymbol{\mu} _e \psi _e \psi _v d\tau_e d\tau_n \approx \int{ \psi _v'^ * } \psi _vd\tau_n \int { \psi _e'^ * } \boldsymbol{\mu} _e \psi _e d\tau_e .

La factorisation serait exacte si l'intégrale \int { \psi _e'^ * } \boldsymbol{\mu} _e \psi _e d\tau_e sur les coordonnées spatiales des électrons n'était pas dépendante des coordonnées nucléaires. Cependant, dans l'approximation Born-Oppenheimer, \psi_e\, et \psi'_e\, dépendent (paramétriquement) des coordonnées nucléaires, et donc l'intégrale (une surface de transition dipolaire) est une fonction des coordonnées nucléaires. La dépendance étant habituellement peu marquée, la négliger (c'est-à-dire le postulat de l'indépendance de la surface de transition dipolaire par rapport aux coordonnées nucléaires, appelée approximation de Condon) est parfois permise.

La première intégrale après le signe plus est égale à zéro car les fonctions d'ondes électroniques des différents états sont orthogonales. Il reste donc le produit de trois intégrales. La première est l'intégrale de recouvrement vibrationnel, aussi appelée facteur Franck-Condon. Les deux intégrales restantes contribuant à la probabilité d'amplitude déterminent les lois de sélection électronique spatiales et de spin.

Le principe Franck-Condon étant un postulat sur les transitions vibrationnelles permises entre deux états électroniques différents, d'autres règles de sélection quantiques peuvent diminuer la probabilité d'une transition, voire l'interdire. Les règles de sélection rotationnelles ont été négligées dans la démonstration ci-dessus. Les contributions rotationnelles peuvent être observées dans les spectres de gaz mais sont très fortement atténuées dans les liquides et solides.

Il devrait être clair à ce stade que la formulation quantique du principe Franck-Condon est le résultat d'une série d'approximations, principalement sur la transition électrique dipolaire et la prise en compte de l'approximation Born-Oppenheimer. Les transitions dipolaires magnétiques et électroniques des quadrupolaires électriques plus faibles, avec la validité incomplète de la factorisation de la fonction d'onde totale dans les fonctions d'ondes nucléaires, électroniques spatiales et les spins, impliquent que les lois de sélection, incluant le facteur Franck-Condon, ne sont pas strictement suivies. Pour toute transition donnée, la valeur de P est déterminée par toutes les règles de sélection, bien que la sélection de spin corresponde à la plus grande contribution, suivie par les règles de sélection électroniques. Le facteur Franck-Condon ne module que faiblement l'intensité des transitions, c'est-à-dire qu'il contribue avec un facteur de l'ordre de 1 à l'intensité des bandes dont l'ordre de grandeur est déterminée par d'autres lois de sélection. Le tableau ci-dessous donne l'intervalle des coefficients d'extinction pour les combinaisons possibles de règles de sélection d'orbitales et de spins permis ou non.

Intensités des transitions électroniques
Intervalle des valeurs (ε) des coefficients d'extinctions (mol-1.cm-1)
Permis en spin et orbitale 103 à 105
Permis en spin, interdit en orbitale 100 à 103
Interdit en spin, permis en orbitale 10-5 à 100

Extension du principe Franck-Condon en spectroscopie

Le principe Franck-Condon, dans sa forme canonique, s'applique seulement aux modifications des niveaux vibrationnels d'une molécule dans le cas d'une modification des niveaux électroniques par absorption ou émission d'un photon. L'intuition physique qui sous-tend ce principe est guidée par l'idée que les coordonnées atomiques des atomes constituants la molécule n'ont pas le temps de changer durant la brève période de temps prise pour la transition électronique. Néanmoins, cette intuition physique peut être (et l'est) étendue de manière routinière aux interactions entre des molécules émettrices ou réceptrices de lumière (chromophores) et leur environnement. Les extensions du principe Franck-Condon sont appropriées dans la mesure où ces molécules interagissent parfois fortement avec les molécules les entourant, particulièrement dans les liquides et solides, et ces interactions modifient les coordonnées nucléaires du chromophore de manière tout à fait analogue aux vibrations moléculaires considérées dans le principe Franck-Condon.

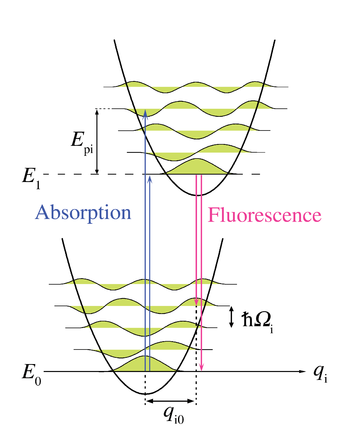Figure 5. Diagramme d'énergie d'une transition électronique avec couplage aux phonons selon la coordonnée réactionnelle q i, un mode normal du réseau. Les flèches montantes représentent l'absorption sans phonon et avec quatre phonons. Les flèches descendantes représentent le processus symétrique en émission.

Principe Franck-Condon pour les phonons

Article détaillé : Raie zéro-phonon et bande satellite phonon.

L'analogie Franck-Condon la plus immédiate est due à l'interaction des phonons - quanta du réseau cristallin - avec les transitions électroniques des chromophores inclus dans le réseau comme impuretés. Dans ce cas, les transitions vers les niveaux électroniques les plus élevés peuvent se produire lorsque l'énergie du photon correspond à l'énergie d'une transition purement électronique ou à l'énergie d'une transition purement électronique plus l'énergie d'un ou plusieurs phonons de réseau. Dans l'approximation des températures basses, l'émission se produit du niveau zéro-phonon de l'état excité au niveau zéro-phonon de l'état fondamental ou vers des niveaux de phonons plus élevés de l'état fondamental. Comme pour le principe Franck-Condon, la probabilité des transitions impliquant des phonons est déterminée par la superposition des fonctions d'ondes phononiques dans les niveaux d'énergie initial et final. Pour le principe de Franck-Condon appliqué aux transitions de phonons, l'axe horizontal de la figure 1 est remplacé figure 5 par la coordonnée configurationnelle pour un mode normal. L'énergie potentiel du mode de réseau qi dans la figure 5 est représentée comme celle d'un oscillateur harmonique, et l'espacement entre niveaux de phonons (\hbar \Omega _i) est déterminée par les paramètres de réseau. L'énergie des phonons simples étant généralement assez faible, les transitions de zéro ou peu de phonons peuvent être observées seulement à des températures en dessous de 40 kelvins.

Principe Franck-Condon pour la solvatation

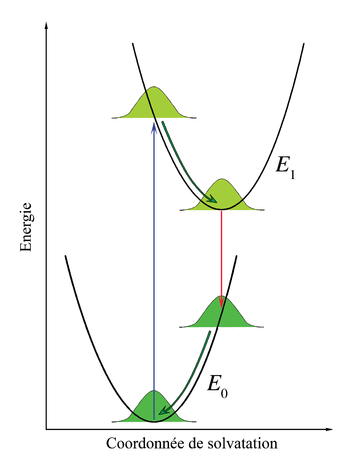Figure 6. Diagramme d'énergie illustrant le principe Franck-Condon appliqué à la solvatation des chromophores. Les courbes paraboliques de potentiel symbolisent l'énergie d'interaction entre les chromophores et le solvant. Les courbes gaussiennes représentent la distribution de cette énergie d'interaction.

Les considérations Franck-Condon peuvent être aussi appliquées aux transitions électroniques des chromophores dissouts dans des liquides. Dans cette perspective, les niveaux vibrationnels des chromophores, comme les interactions des chromophores avec les phonons du liquide, continuent à la structure des spectres d'absorption et d'émission, mais ces effets sont considérés comme séparés et indépendants.

Considérons les chromophores comme entourés par les molécules du solvant. Ces molécules peuvent interagir avec les chromophores, particulièrement si les molécules du solvant sont polaires. L'association entre le solvant et le soluté est appelée solvatation et est une interaction stabilisante, ce qui signifie que les molécules de solvant peuvent se déplacer et tourner jusqu'à ce que l'énergie d'interaction soit minimisée. L'interaction en elle-même mets en jeu des forces électrostatiques et de van der Waals et peut parfois comprendre des liaisons hydrogène. Les principes Franck-Condon peuvent être appliqués lorsque les interactions entre le chromophore et les molécules de solvant l'entourant sont différentes entre états fondamentaux et excités. Cette modification dans l'interaction peut se produire, par exemple, en raison d'une différences des moments dipolaires entre les deux états. Si le chromophore initialement dans son état fondamental est proche de l'équilibre avec les molécules le solvatant puis absorbe un photon qui l'excite, son interaction avec le solvant sera éloignée de l'équilibre dans l'état excité. Cet effet est analogue avec le principe Franck-Condon original : la transition électronique est très rapide comparée avec le mouvement des noyaux - le réarrangement des molécules de solvant dans le cadre d'une solvatation. On peut alors parler de transition verticale, mais la coordonnée horizontale est maintenant l'espace d'interaction solvant-soluté. Cet axe de coordonnée est parfois appelé « axe de solvatation » et représente, plus ou moins abstraitement, tout ce qui correspond aux dimensions pertinentes du mouvement de l'ensemble des molécules de solvant interagissant.

Dans le principe Franck-Condon original, après la transition électronique, les molécules se trouvant dans des états vibrationnels plus énergétiques commencent immédiatement à relaxer vers l'état vibrationnel le plus bas. Dans la cas de la solvatation, les molécules de solvant essaieront immédiatement de se réarranger afin de minimiser l'énergie d'interaction. Le taux de relaxation du solvant dépend de sa viscosité. Considérant que le temps de relaxation du solvant est court comparé au temps de vie de l'état électronique excité, l'émission se fera depuis l'état d'énergie le plus bas de l'état électronique excité du solvant. Pour des solvants à petites molécules, comme l'eau ou le méthanol à température ambiante, le temps de relaxation du solvant est de l'ordre de quelques dizaines de picosecondes alors que les temps de vie des états excités des chromophores vont des quelques picosecondes à quelques nanosecondes. Immédiatement après la transition vers l'état électronique fondamental, les molécules de solvant doivent aussi se réarranger afin de s'accorder à la nouvelle configuration électronique du chromophore. La figure 6 illustre le principe Franck-Condon appliqué à la solvatation. Lorsque la solution est éclairée par une lumière correspondant à l'énergie de transition électronique, certains chromophores se trouveront dans l'état excité. Dans ce groupe, il y aura une distribution statistique des énergies d'interaction solvant-chromophore, représentée dans la figure par une fonction de distribution gaussienne. L'interaction solvant-chromophore est dessinée comme étant un potentiel parabolique dans les deux états électroniques. Les transitions électroniques étant essentiellement instantanées sur l'échelle de temps du mouvement du solvant (flèche verticale), l'ensemble des chromophores dans un état excité est immédiatement loin de l'équilibre. Le réarrangement des molécules de solvant selon la nouvelle courbe d'énergie potentielle est représentée par le flèches courbes dans la figure 6. Remarquons que lorsque les transitions électroniques sont quantifiées, l'énergie d'interaction chromophore-solvant est traitée comme un continuum classique en raison du nombre important de molécules concernées. Bien que l'émission soit décrite comme allant se produire à partir du minimum du potentiel d'interaction solvant-chromophore de l'état excité, une émission significative peut se produire avant d'atteindre l'équilibre lorsque la viscosité du solvant est importante ou que le temps de vie de l'état excité est court. La différence d'énergie entre les photons émis et absorbés décrits dans la figure 6 est la contribution de la solvatation au déplacement de Stokes.

Références

  • Franck, J., « Elementary processes of photochemical reactions », dans Transactions of the Faraday Society, vol. 21, 1926, p. 536–542 [lien DOI]  Link
  • Condon, E., « A theory of intensity distribution in band systems (Meeting abstract) », dans Physical Review, vol. 27, 1926, p. 640 
  • Condon, E., « A theory of intensity distribution in band systems », dans Physical Review, vol. 28, 1926, p. 1182–1201 [lien DOI]  Link
  • Condon, E., « Nuclear motions associated with electron transitions in diatomic molecules », dans Physical Review, vol. 32, 1928, p. 858–872 [lien DOI]  Link
  • Birge, R. T., « The band spectra of carbon monoxide », dans Physical Review, vol. 28, 1926, p. 1157–1181 [lien DOI]  Link
  • Noyes, W. A., « The correlation of spectroscopy and photochemistry », dans Reviews of Modern Physics, vol. 5, 1933, p. 280–287 [lien DOI]  Link
  • Coolidge, A. S, James, H. M. and Present, R. D., « A study of the Franck-Condon Principle », dans Journal of Chemical Physics, vol. 4, 1936, p. 193–211 [lien DOI]  Link
  • Gerhard Herzberg, The spectra and structures of simple free radicals, New York, Dover, 1971 (ISBN 0-486-65821-X) 
  • Daniel C. Harris, Michael D. Bertolucci, Symmetry and spectroscopy, New York, Dover, 1978 (ISBN 0-486-66144-X) 
  • Peter F. Bernath, Spectra of Atoms and Molecules (Topics in Physical Chemistry), Oxford, Oxford University Press, 1995 (ISBN 0-19-507598-6) 
  • Peter Atkins, R. S. Frieman, Molecular Quantum Mechanics, Oxford, Oxford University Press (ISBN 0-19-855947-X) 

Voir aussi

Liens externes



Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Principe Franck-Condon de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • principe de Franck-Condon — Franko ir Kondono principas statusas T sritis fizika atitikmenys: angl. Franck Condon principle vok. Franck Condon Prinzip, n rus. принцип Франка Кондона, m pranc. principe de Franck et Condon, m; principe de Franck Condon, m …   Fizikos terminų žodynas

  • Franck-Condon principle — Franko ir Kondono principas statusas T sritis fizika atitikmenys: angl. Franck Condon principle vok. Franck Condon Prinzip, n rus. принцип Франка Кондона, m pranc. principe de Franck et Condon, m; principe de Franck Condon, m …   Fizikos terminų žodynas

  • Franck-Condon-Prinzip — Franko ir Kondono principas statusas T sritis fizika atitikmenys: angl. Franck Condon principle vok. Franck Condon Prinzip, n rus. принцип Франка Кондона, m pranc. principe de Franck et Condon, m; principe de Franck Condon, m …   Fizikos terminų žodynas

  • Condon (homonymie) —  Pour l’article homophone, voir Condom. Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Condon est un nom propre. Il fut celui d une ancienne commune de l Ain, faisant maintenant partie de Andert… …   Wikipédia en Français

  • principe de Franck et Condon — Franko ir Kondono principas statusas T sritis fizika atitikmenys: angl. Franck Condon principle vok. Franck Condon Prinzip, n rus. принцип Франка Кондона, m pranc. principe de Franck et Condon, m; principe de Franck Condon, m …   Fizikos terminų žodynas

  • Edward Condon — Edward Uhler Condon (né le 2 mars 1902 à Alamogordo mort le 26 mars 1974 à Boulder) était un physicien nucléaire américain, pionnier de la mécanique quantique, qui participa au développement du radar et des armes nucléaires pendant la Seconde… …   Wikipédia en Français

  • James Franck — Pour les articles homonymes, voir Franck. James Franck James Franck (26 août 1882 à Hambourg, allemagne …   Wikipédia en Français

  • Raie zéro-phonon et bande satellite phonon — Figure 1. Représentation schématique du profil d une excitation électronique. La partie étroite à la fréquence ωˈ est la raie zéro phonon, la partie plus large est la bande satellite phonon. Les positions relatives des deux composantes lors d une …   Wikipédia en Français

  • Fluorescence Induite par Laser — Sommaire 1 Présentation générale 2 Principe physique 3 Ensemencement 4 Acquisition du signal …   Wikipédia en Français

  • Fluorescence induite par laser — Sommaire 1 Présentation générale 2 Principe physique 3 Ensemencement 4 Acquisition du signal …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”